
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Следует ли из существования производной функции в точке ее непрерывность в этой точке? Ответ обоснуйте. ⇐ ПредыдущаяСтр 4 из 4 Если функция U=f(x) дифференцирована в некоторый точке x=x0, то она непрерывна в этой точке. Это условие необходимое, но недостаточное. Доказательство: пусть функция u= f(x) дифференцирована, тогда существует 30. Докажите теорему о производной суммы двух функций.
31. Докажите теорему о производной произведения двух функций.
Дайте определение дифференциала функции Дифференциалом функции в точке х0 называется главная линейная часть приращения функции в этой точке При Dx"0, dy=y’Dx или 32.
33. ln(1+0,09)= ln1+1*0.09=0.09 Дайте определение эластичности функции в точке. Найдите эластичность функции Эластичностью функции y = f(x) в точке х0 называется предел Ey = (lnx)’ * x 34. 35. Дайте определение и сформулируйте необходимое условие локального экстремума функции одной переменной. Приведите пример функции, для которой это условие выполнено в некоторой точке, но экстремум отсутствует. Точками локального экстремума явл. точки локального максимума (минимума). Точкой локального максимума точка явл. если существует окрестность т. Мо, в которой для любой точки М(x,y) выполняется неравенство f(M)£f(M0). Необходимое условие: если f’(x,y) имеет частные производные 1-ого порядка в точке локального экстремума M0(x,y), то 37. На рисунке изображен график производной 
Какое из утверждений верно: а) функция б) функция в) функция г) функция д) функция 38. Функция а) б)
в) г)
д)
Рассмотрим. 39. Сформулируйте теорему Ролля. Докажите, что производная функции Пусть ф-ция f(x) непрерывна на отрезке [a;b], дифференцируема на интервале (a;b) и f(a) = f(b), то найдётся хотя бы одна точка
40. Сформулируйте теорему Лагранжа. Докажите, что если Пусть ф-ция f(x) непрерывна на отрезке [a;b], дифференцируема на интервале (a;b), тогда существует точка с О из (a, b) такая, что f(b) − f(a) = f '(c) · (b − a). 41. Используя теорему Лагранжа, докажите, что если Пусть функция у=f(x) имеет f’(x)и.непрерывна на отрезке [a, b]; Тогда существует точка Пусть функция у=f(x) имеет f’(x)и.непрерывна на отрезке [a, b]; Тогда существует точка F'(c) > 0 -> 42. Функция а) Какое наименьшее количество нулей может иметь данная функция на указанном промежутке? 2 нуля (достаточно отметить точки f(-10) f(-1) и f(3) на графике чтобы это понять) б) Существует ли такое значение в) Существуют ли на промежутке г) Если у функции |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 170. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 =а, тогда
=а, тогда  =а+a(x), где a(x) – бмп. Тогда Dy=Dxа + Dxa(x),
=а+a(x), где a(x) – бмп. Тогда Dy=Dxа + Dxa(x),  Dy =
Dy = 







 в точке
в точке  . Используя дифференциал, найдите приближенное значение величины:
. Используя дифференциал, найдите приближенное значение величины: .
. 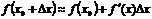
 =
=  , 25= x0, 0,12=Dx => f(x)=
, 25= x0, 0,12=Dx => f(x)=  => f’(x)=1/10
=> f’(x)=1/10 5+0.1*0.12=5.012
5+0.1*0.12=5.012 в точке
в точке  :
: .
. ,
,  . Ey = - x / (x+1). Ey (4)= -4/5
. Ey = - x / (x+1). Ey (4)= -4/5 ,
,  . Ey = 3x*ln3*x / 3x = x * ln3. Ey (5)=5ln3
. Ey = 3x*ln3*x / 3x = x * ln3. Ey (5)=5ln3 . Примером является х3, х0=0 – точка перегиба, но не экстремума.
. Примером является х3, х0=0 – точка перегиба, но не экстремума. функции
функции 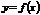 .
.
 убывает для
убывает для 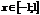 ; нет
; нет ; нет, только на х на интервале [-2; 0). Точка 0 – дочка локального максимума.
; нет, только на х на интервале [-2; 0). Точка 0 – дочка локального максимума. ; нет
; нет ; нет, максимум
; нет, максимум и при
и при 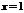 . Дифференцируема, так как существует значение производной.
. Дифференцируема, так как существует значение производной. такова, что для всех действительных значений
такова, что для всех действительных значений 
 ,
,  и
и  . Какой из представленных графиков может быть графиком функции
. Какой из представленных графиков может быть графиком функции  ?
?




 значит, что ф-ция находится под Ох (то есть ф-ция приминает только отрицательные значения при любом значении аргумента).
значит, что ф-ция находится под Ох (то есть ф-ция приминает только отрицательные значения при любом значении аргумента).  значит, что функция убывает во всех значениях своего аргумента. И, наконец,
значит, что функция убывает во всех значениях своего аргумента. И, наконец,  означает, что ф-ция вогнута. Всем этим условиям соответствует только б)
означает, что ф-ция вогнута. Всем этим условиям соответствует только б)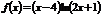 обращается в нуль в некоторой точке интервала
обращается в нуль в некоторой точке интервала  .
. , в которой
, в которой  .
. , f(0)=0, f(4)=0. Ф-ция непрерывна и диф-ма на промежутке. В таком случае по теореме Ролля на этом промежутке существует экстремум ф-ции.
, f(0)=0, f(4)=0. Ф-ция непрерывна и диф-ма на промежутке. В таком случае по теореме Ролля на этом промежутке существует экстремум ф-ции. на интервале
на интервале  , то функция
, то функция  постоянна на этом интервале.
постоянна на этом интервале. .
.  =>
=> 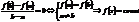 .
. на интервале
на интервале  , то функция
, то функция  такая, что f(b) − f(a) = f '(c) · (b − a).
такая, что f(b) − f(a) = f '(c) · (b − a). возрастает.
возрастает. . Известно, что
. Известно, что 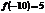 ,
,  и
и  .
. , что
, что  ? Да, так как существует f(-10)=5 и f(-1)=-1. Функция непрерывна, и поэтому она должна проходить в точке f(c)=2.
? Да, так как существует f(-10)=5 и f(-1)=-1. Функция непрерывна, и поэтому она должна проходить в точке f(c)=2.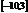 у функции
у функции  горизонтальные касательные? Да, так как она сначала убывает, а потом возрастает. В точке смены убывания на возрастание (f’(x)=0) у функции будет горизонтальная касательная.
горизонтальные касательные? Да, так как она сначала убывает, а потом возрастает. В точке смены убывания на возрастание (f’(x)=0) у функции будет горизонтальная касательная. есть только одна точка экстремума на
есть только одна точка экстремума на  , будет ли она точкой максимума или минимума? Точкой минимума, так как ф-ция меняет свое поведение с убывания на возрастание.
, будет ли она точкой максимума или минимума? Точкой минимума, так как ф-ция меняет свое поведение с убывания на возрастание.