Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Описательные статистики и процентилиНа рис. 6.8 представлены результаты выполнения шагов 5г и 5д. Описательные статистики рассматриваются подробнее в главе 7, поэтому мы не станем обсуждать их здесь. Обратите внимание, что если в вывод результатов включены асимметрия (Skewness) и эксцесс (Kurtosis), то для них по умолчанию вычисляется стандартная ошибка (Std. Error of Skewness и Std. Error of Kurtosis соответственно). ОТМЕТКА2 3.50 3.75 4.00 4.25 4.50 4.75 3.63 3.88 4.13 4.38 4.63 4.88 ОТМЕТКА2 Рис. 6.7. Фрагмент окна вывода после выполнения шага 56 ОТМЕТКА2
OTMETKA2
Рис. 6.8. Фрагменты окна вывода после выполнения шагов 5г и 5д Что касается процентилей (Percentiles), то их можно трактовать следующим образом: для переменной отметка2 10 % значений не превышают 3,855 (10 % учащихся имеют отметку не выше 3,855; 30 % значений не превышают 4,05 (30 % учащихся имеют отметку не выше 4,05), и т. д. · Описательные статистики. Медиана(термин был впервые введен Гальтоном, 1882) – это значение признака, которое делит упорядоченное (ранжированное) множество данных пополам так, что одна половина всех значений оказывается меньше медианы, а другая - больше. Медианное значение помогает проверять насколько представительным является среднее значение.  Медиана менее подвержена искажению ввиду наличия очень больших или маленьких значений в ряде данных. медиана – это 50-тый процентиль в группе данных.
Дисперсия– мера изменчивости для метрических данных, пропорциональная сумме квадратов отклонений измеренных значений от их арифметического среднего. Чем больше изменчивость в данных, тем больше отклонения значений от среднего, тем больше величина дисперсии. Дисперсию используют при вычислении каждого из полученных измерений. Вычисляются значения отклонений
Для вычисления дисперсии не нужно вычислять среднее. Дисперсия при сгруппированных данных вычисляется по такой же формуле, но
i изменяется от 1 до k, где k – количество разных значений Стандартное отклонение: Для унимодальных симметричных распределений почти 70% значений лежит в интервале Свойства дисперсии: 1. Влияние на дисперсию увеличения каждого значения на какую либо константу:
2. Изменение дисперсии при умножении каждого исходного значения на константу:
3. Дисперсия объединенной группы:
где:
Стандартное отклонение – положительное значение квадратного корня из дисперсии. На практике чаще используется именно стандартное отклонение, а не дисперсия, так как выражает изменчивость в исходных единицах измерения признака. Стандартное отклонение (термин был впервые введен Пирсоном, 1894) - это широко используемая мера разброса или вариабельности (изменчивости) данных. Стандартное отклонение популяции определяется формулой: = [(xi-)2/N]1/2 где
Выборочное стандартное отклонение или оценка стандартного отклонения вычисляется по формуле: s = [(xi-x-bar)2/n-1]1/2 где
См. также Описательные статистики - Вводный обзор. Стандартное отклонение (σ или SD) - показатель степени разброса отдельных индивидуальных наблюдений относительно этого среднего, то есть, мера внутригрупповой изменчивости данного признака. В качестве такого показателя для каждого из m признаков вычисляют дисперсию (s2): Минимум и максимум — это минимальное и максимальное значения переменной. Размах (разброс)– это разность между максимальной и минимальной величинами конкретного вариационнго ряда. Чем сильнее варьирует измеряемый признак, тем больше величина размаха, и наоборот. Размах – это разность максимального и минимального значений в группе. Включающий размах – это разность между естественной верхней границей интервала, включая наибольшее значение, и естественной нижней границей, включая наименьшее значение интервала. Размах от 90-го до 10-го процентеля: D = P90 – P10 . Эта мера более стабильна, чем предыдущая, так как на нее влияет множество значений. Полу-междуквантильный размах: Сумм -это общая численность переменных. Эксцесс (вариация)– мера плосковершинности или остроконечности графика распределения измеренного признака. Эксцесс – это мера крутости кривой распределения. Унимодальная кривая распределения может быть островершинной, плосковершинной, средне вершинной. Эксцесс для стандартных данных:
Эти четыре момента составляют набор особенностей распределения при анализе данных. Нормальное распределение Нормальное распределение лучше всего описывается кривой созданной ДеМуавром по следующей формуле:
где U – высота кривой над осью x, t и μ – числа, которые определяют положение кривой относительно числовой оси и регулируют ее размах. Для μ=0, t =1 график принимает вид: Эта кривая при μ=0, t =1 получила статус стандарта, ее называют единичной нормальной кривой, то есть любые собранные данные стремятся преобразовать так, чтобы кривая их распределения была максимально близка к этой стандартной кривой. Созданы статистические таблицы со значениями площади под единичной нормальной кривой влево от любой точки на оси z в (-3; 3). Общая площадь под кривой равна 1. И все остальные площади рассматривают как процент от целого. Асимметрия– степень отклонения графика распределения частот от симметричного вида относительно среднего значения. Асимметрия – это свойство распределения частот. На практике симметричные полигоны и гистограммы не встречаются и чтобы выявить и оценить степень асимметрии, вводят следующую меру:
В единицах стандартного отклонения асимметрия равна:
Асимметрия бывает положительной и отрицательной. Положительная сдвигается влево, а отрицательная – вправо. Чтобы упростить вычисление Ass можно использовать следующую формулу:
Асимметрия в этом уравнении принимает значения от –3 до +3
· Сравнение двух групп. 1.Сравнить успеваемость юношей и девушек в 11 классе, т.е. две независимые выборки с помощью Критерия МаннаУитни (MannWhitney), или U-критерия (ориентированый на распределения, отличные от нормальных).По назначению аналогичен t-критерию для независимых выборок (ориентированый на нормальные и близкие к ним распределения). При реализации метода программа сначала ранжирует все объекты без учета принадлежности к сравниваемым группам, а затем вычисляет средние ранги для каждой из В меню Analyze (Анализ) выберите команду Nonparametric Tests ► 2 Independent Samples (Непараметрические методы ►Две независимые выборки), чтобы открыть диалоговое окно Two-Independent Samples Test (Критерий для двух независимых выборок) (рис. 3) ► Для применения метода :переместите переменную отметка2 в списокTest Variable List (Список тестируемых переменных) ► Переместите переменную пол в полоGrouping Variable (Группирующая переменная) ► В диалоговом окне Define Groups (Определение групп), В поле Group 1 (Группа 1) введите значение 1, в поле Group 2 (Группа 2), введите значение 2 и щелкните на кнопке Continue (Продолжить), чтобы вернуться в диалоговое окно Two-Independent Samples Test (Критерий для двух независимых выборок). ►О К. Результаты работы программы: Средний ранг (Mean Rank) для девушек равен 56,21, а для мужчин 41,56. Это значит, что у девушек успеваемость выше, чем у юношей. Величина U-критерия (MannWhitney U) равна 841. Значение Z является нормализованным, связанным с уровнем значимости р = 0,014. Поскольку величина уровня значимости (Asymp. Sig. (2-tailed)) меньше 0,05, мы можем быть уверены в достоверности вывода о том, что успеваемость девушек действительно выше успеваемости юношей. 1. Практическая часть. Работа со статистическим пакетом. · Создание базы данных. Программирование. особенности копинг-стратегий (дистанцироваине, бегство – избегание) у одиноких пожилых людей и пожилых людей проживающих в семье. Заносим данные в файл SPSS. Рисунок 1
Окно Представление Переменные
Рисунок 2. Представление Данные (Пожилые люди, проживающие в семье)
Рисунок 3 (Одинокие пожилые люди)
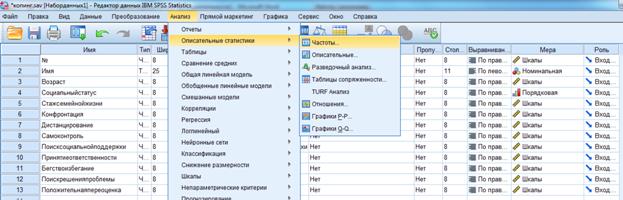
· Распределение первичных результатов. Расчет накопленных частот и процентной суммы накопленных частот. Анализ-Дискриптивные статистики-Частоты (Отметить галочку гистограмма), описать полученные результаты. Ход работы проиллюстрировать в скриншотах (см. ниже образец).
Рисунок 4
· Описательные статистики.
Этапы работы:
Рисунок 5.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 439. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
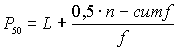
 и чтобы при суммировании
и чтобы при суммировании  не потерять величины этих отклонений, разница возводится в квадрат, поскольку мы оцениваем отклонение каждого измерения, делим на количество измерений. Обозначается дисперсия как
не потерять величины этих отклонений, разница возводится в квадрат, поскольку мы оцениваем отклонение каждого измерения, делим на количество измерений. Обозначается дисперсия как  .
.
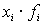

 .
.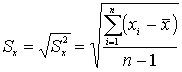
 .
. , после выполнения математических операций убеждаемся, что дисперсия не изменяется.
, после выполнения математических операций убеждаемся, что дисперсия не изменяется. , то есть дисперсия увеличивается на квадрат константы.
, то есть дисперсия увеличивается на квадрат константы.

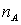 - количество значений группы А, для Б аналогично
- количество значений группы А, для Б аналогично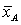 - среднее группы А, для Б аналогично
- среднее группы А, для Б аналогично
 . Включающий размах отличается от исключающего на единицу.
. Включающий размах отличается от исключающего на единицу. , Q используется в распределениях, которые симметричны относительно медианы и среднего, для корректировки границ.
, Q используется в распределениях, которые симметричны относительно медианы и среднего, для корректировки границ.

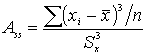



 двух групп Чем выше средний ранг группы, тем выше ее успеваемость После определения средних рангов определяется р-уровень.
двух групп Чем выше средний ранг группы, тем выше ее успеваемость После определения средних рангов определяется р-уровень.