
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчёт статически неопределимых систем методом сил в матричной формеСистема канонических уравнений метода сил (16.4) в матричной форме запишется: dX + DF = 0. (16.20) d – матрица перемещений по направлению усилий в удалённых связях Хi в единичных состояниях основной системы метода сил, или матрица внешней податливости основной системы метода сил по направлению Xi (i = 1, 2, …, n).
Число строк и столбцов этой матрицы равно степени статической неопределимости сооружения n, т.е. матрица d – это квадратная матрица. С учётом теоремы о взаимности перемещений матрица d симметрична. В силу разрешимости системы уравнений (16.20) матрица внешней податливости основной системы метода сил является невырожденной, так как её определить не равен нулю (det d ¹ 0). Х – матрица усилий в лишних связях сооружения, или матрица неизвестных метода сил.
DF – матрица перемещений по направлению неизвестны метода сил в основной системе от заданного силового воздействия, или матрица свободных членов системы канонических уравнений метода сил.
Число строк в матрицах Х и DF равно степени статической неопределимости сооружения n, а число столбцов – числу комбинаций внешних нагрузок р (постоянной и временных). Элементы матриц d и DF – это перемещения в основной системе метода сил по направлению усилий в удаленных связях Xi, соответственно, от единичных значений этих усилий и заданной нагрузки. Упомянутые перемещения dii, dij, DiF можно вычислить в матричной форме, используя соотношение (13.18): d = LT B L, (16.21) DF = LT B LF. (16.22) L – матрица необходимых для расчёта сооружения на силовое воздействие внутренних усилий (изгибающих моментов, поперечных и продольных сил) в основной системе метода сил от X1 = 1, X2 = 1, …, Xj = 1, …, Xn = 1.  L = [L1 L2 … Lj … Ln], Число столбцов матрицы L равно числу неизвестных метода сил n, а число строк блоков Mj, Qj, Nj этой матрицы определяется характером внешней нагрузки и числом грузовых участков сооружения. Для k-го грузового участка с равномерно распределённой нагрузкой
Здесь в и е – концевые сечения грузового участка (начало и конец), с – среднее сечение грузового участка. Для k-го грузового участка, на котором распределённой нагрузки нет
Для участка с произвольно ориентированной по отношению к оси стержня равномерно распределённой нагрузкой
для грузового участка с такой же нагрузкой, но не перпендикулярной его оси
Если равномерно распределённая нагрузка перпендикулярна оси стержня, то продольную силу на таком грузовом участке берут в одном, произвольно взятом, сечении. При отсутствии нагрузки поперечную и продольную силы также фиксируют в одном сечении грузового участка. В соотношении (16.22) LF – матрица внутренних усилий в основной системе метода сил от заданной нагрузки. LF = [LF1 LF2 … LFj … LFp], Число строк в блоках MFj, QFj, NFj матрицы LF также зависит от вида нагрузки, количества грузовых участков заданной системы и совпадает с числом строк блоков Mj, Qj, Nj матрицы L. Количество столбцов матрицы LF равно числу комбинаций силовых воздействий р. В матричных соотношениях (16.21) и (16.22) В – матрица внутренней упругой податливости сооружения.
ВМ – матрица упругой податливости, учитывающая изгибные деформации элементов сооружения. Для грузового участка с постоянной изгибной жёсткостью поперечного сечения (EJk = const) при наличии на нём равномерно распределённой нагрузки
при отсутствии нагрузки –
BQ – матрица упругой податливости, учитывающая деформации сдвига элементов системы. На k-ом участке с равномерно распределённой нагрузкой в случае GAk = const
без такой нагрузки –
BN – матрица упругой податливости, учитывающая деформации растяжения-сжатия сооружения. Если равномерно распределённая нагрузка не перпендикулярна оси k-го грузового участка, то
если же такого рода нагрузка действует перпендикулярно оси грузового участка или вообще отсутствует на нём, то
Из системы канонических уравнений (16.20) получим матрицу неизвестных метода сил: X = –d-1 DF. (16.23) d-1 – матрица, обратная по отношению к матрице внешней податливости d. Из линейной алгебры известно, что d × d-1 = Е, где Е – единичная матрица. Подставляя соотношение (16.21) и (16.22) в матричное выражение (16.23), получим: X = –(LT B L)-1 (LT B LF). (16.24) Вычислив матрицу усилий в лишних связях сооружения Х и используя матрицы L и LF, элементы которых есть внутренние усилия (изгибающие моменты, поперечные и продольные) от X1 = 1, X2 = 1, …, Xj = 1, …, Xn = 1 и заданной нагрузки, в соответствии с принципом независимости действия сил, получим:
S – матрица внутренних усилий (изгибающих моментов M(F), поперечных Q(F) и продольных N(F) сил в заданном сооружении от силового воздействия. Число строк этой матрицы совпадает с числом строк матрицы L и LF, а число столбцов – с числом столбцов матрицы LF, т.е. с количеством комбинаций внешних воздействий. С учётом выражения (16.24) матричное соотношение (16.25) в окончательной форме запишется: S = LF – L(LTBL)-1(LTBLF). (16.26) Для кинематической проверки расчёта заданного статически неопределимого сооружения на силовое воздействие производится сопряжение окончательных эпюр внутренних усилий, описываемых элементами матрицы S, с эпюрами внутренних усилий в единичных состояниях основной системы метода сил, описываемых элементами матрицы L. Если расчёт произведён правильно, то результат сопряжения вышеупомянутых эпюр в матричной форме даст нулевую матрицу, т.е. LT B S = 0. (16.27) В расчётах плоских статически неопределимых рамных и балочных систем в соотношениях (16.26) и (16.27) матрицы L, LF будут содержать блоки, учитывающие только изгибающие моменты, а матрица В – только элементы, соответствующие изгибным деформациям сооружения. С учётом данного обстоятельства, когда L = M, LF = MF, B = BM, S = M(F), имеем M(F) = MF – M(MT BM M)-1(MT BM MF), (16.28) MT BM M(F) = 0. (16.29 |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 372. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. .
. .
. .
. .
.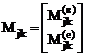 .
. ,
, .
. .
. .
. ,
, .
. ,
, .
. ,
, .
.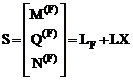 . (16.25)
. (16.25)