
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Понятие о силе. Классификация сил.Стр 1 из 5Следующая ⇒ Часть II Лекция 4. Напряжения и деформации твёрдого тела Осевое растяжение – сжатие. Закон Гука и коэффициент Пуассона ………………...……..4 Лекция 5. Диаграмма растяжения малоуглеродистой стали. Диаграммы условных и истинных напряжений…………………………………..11 Лекция 6. Статически неопределимые стержневые системы…………….……17 Лекция 7. Теория напряженного состояния. Касательные и нормальные напряжения по наклонным и двум взаимно перпендикулярным площадкам………...…………………………………………………...23 Лекция 8. Закон парности касательных напряжений. Понятие о главных площадках и главных напряжениях. Круги Мора…………………..27 Лекция 9. Теории прочности……………………………………………………..33 Лекция 10. Изгиб. Изгибающий момент и перерезывающая сила. Дифференциальные зависимости при изгибе. Построение эпюр поперечных сил и изгибающих моментов…………………………..36 Лекция 11. Нормальные и касательные напряжения при изгибе. Условие прочности и выбор сечения балки ……………………….38 Лекция 12. Сдвиг. Напряжения и деформации. Закон Гука при сдвиге. Кручение. Проверка на жесткость и прочность. Выбор сечения валов..………………………………………………………………...43 Лекция 13. Сложное сопротивление. Косой изгиб. Поперечный изгиб … …..52 Лекция 14. Сложное сопротивление. Внецентренное растяжение-сжатие. Изгиб с кручением …………………………………………………..56 Лекция 15. Устойчивость сжатых систем. Формула Эйлера. Способы закрепления концов стержней………………………………………61 Лекция 16. Гибкость стержней. Формула Ясинского. Подбор типа сечения  стержней и материала………………………………………………63
МЕХАНИКА ВВЕДЕНИЕ Основной целью изучения дисциплины «Механика» (разделы «Теоретическая механика» и «Сопротивление материалов») является приобретение студентами знаний и навыков в области теоретической механики, расчетов отдельных элементов конструкций и сооружений на прочность, жесткость и устойчивость, основ конструирования элементов и законченных конструкций горных машин. Данная дисциплина является общепрофессиональной и должна рассматриваться как теоретическая база, на основе которой производятся расчеты и проектирование отдельных элементов и конструкций инженерных сооружений и горных машин. Задача дисциплины заключается в том, чтобы будущий специалист мог выполнить инженерные расчеты, обеспечивающие надежность, долговечность и безопасность инженерных конструкций, а также овладеть навыками по конструированию основных блоков горных машин. В результате освоения программы курса студент должен: ·Знать основные положения теоретической механики абсолютно жесткого тела – статики, кинематики и динамики; уметь составлять и решать задачи по анализу движения твердого тела. · знать теоретические основы сопротивления материалов; основные понятия, правила и порядок расчетов элементов конструкций на прочность, жесткость и устойчивость; критерии выбора конструкционных материалов и конструктивных форм; · уметь самостоятельно выбирать расчетные схемы, производить расчеты типовых элементов конструкций и сооружений, сравнивать и отыскивать оптимальные варианты решения, связывать воедино инженерную постановку задачи, расчет и проектирование; пользоваться ГОСТами; · иметь представление о критериях обеспечения высоких показателей надежности, долговечности и безопасности напряженных конструкций и сооружений. ЧАСТЬ 1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. Лекция 1. Основы статики твердого тела. Понятие о силе. Классификация сил. Состояние равновесия или движения материального тела зависит от характера его взаимодействия с другими телами. Величина, являющаяся количественной мерой механического взаимодействия материальных тел, называется силой. Сила есть величина векторная, и ее действие на тело определяется тремя параметрами: численной величиной (модулем силы), направлением и точкой приложения. Силы бывают внешними и внутренними. Внешние силы, являются результатом действия на рассматриваемое тело других тел, при этом механику не интересует физическая природа сил, она изучает лишь количественную сторону их связи с механическим движением. Внешние силы делятся на активные (или заданные) и пассивные (или реактивные). Активные силы не зависят друг от друга, они определяются назначением сооружения и им же воспринимаются. К ним относятся, например, собственный вес сооружения, давление ветра, вес снега, лежащего на крыше, силы инерции и т.д. Пассивными силами являются реакции связи, эти силы не независимы, а являются функцией активных сил и устройства связей (опор). Всякая сила, поскольку источником ее является материя, есть сила объемная. Объемные силы, в зависимости от особенностей передачи силового воздействия на тело, условно заменяют эквивалентными им распределенными и сосредоточенными силами. Силы могут быть распределены по площади (давление снега, воды, газа и т.д.), в этом случае они называются поверхностными, и по длине (собственный вес балки какого-либо перекрытия). Сосредоточенная сила предполагает передачу нагрузки на элемент конструкции через площадку, размеры которой очень малы по сравнению с размерами всего элемента (например, давление колес железнодорожного состава на рельсы). При расчетах, благодаря малости площадки, передающей давление, обычно считают сосредоточенную силу приложенной в точке. Такое приближенное представление вводится лишь для упрощения расчетов, а неточность, вызываемая этим, настолько мала, что ею обычно на практике пренебрегают. Сосредоточенные нагрузки измеряются в единицах силы (ньютонах, килограммах, тоннах); распределенные по площади нагрузки выражаются в единицах силы, отнесенных к единице площади (Н/м2; кг/см2 и т.п.); распределенные по длине элементы - в единицах силы, отнесенных к единице длины (Н/м; т/м и т.д.). Кроме того, силы разделяются на постоянные и временные. К первым относятся такие нагрузки, величина которых не меняется или изменяется весьма незначительно за все время существования конструкции (например, нагрузка на фундамент от собственного веса здания и находящегося в нем оборудования). Переменные нагрузки действуют на конструкцию в течение некоторого промежутка времени, причем у них может изменяться интенсивность и направление, или то и другое вместе (давление ветра, давление снега, давление поезда, идущего по мосту, и т.п.). По характеру действия нагрузки можно разделить на статическиеидинамические. При передаче статических нагрузок на конструкцию все ее части находятся в равновесии, ускорения отсутствуют или настолько малы, что ими можно пренебречь. К числу динамических нагрузок относятся внезапно приложенные (давление колес локомотива, входящего на мост), ударные (забивка свай) и повторно-переменные (циклическое давление газов на поршневую систему в цилиндре двигателя внутреннего сгорания). Силы графически изображаются отрезками прямых линий (векторами), определяющими их величину, положение и направление. За единицу силы в графической статике принимается отрезок прямой АВ в линейной масштабе, соответствующем ее модулю, а направление обозначается стрелкой. Начало отрезка называется точкой приложения силы Прямая, проведенная через точки А и В, называется линией действия силы Сила, заменяющая действие заданной системы сил, называется равнодействующей, а приложенные силы по отношению к их равнодействующей называются составляющими. В случае, когда к системе сил, действующих на тело, приложена сила, равная и противоположно направленная равнодействующей, тело будет находиться в равновесии, а данная сила называться уравновешивающей. Силу в пространстве вполне определяют величины ее проекций на три координатные оси и величины моментов относительно тех же осей.
Аксиомы статики В статике, являющейся составной частью теоретической механики, рассматриваются абсолютно твердые тела, в которых расстояния между каждыми двумя точками остаются при действии сил неизменными, т.к. форма и размеры тела не изменяются. Основные положения статики твердого тела базируются на знании нескольких аксиом, являющихся результатом обобщения человеческого опыта и подтверждаемых экспериментально с большой степенью точности. Аксиома I. Две равные силы, приложенные в одной или разных точках твердого тела, направленные по одной прямой в противоположные стороны, взаимно уравновешиваются; тело при действии этих сил находится в равновесии. Аксиома II. Действие сил, приложенных к телу, не изменится, если присоединить к ним или отнять от них силы, взаимно уравновешивающиеся. Из этих двух начал вытекает следствие: точку приложения силы, действующей на твердое тело, можно переносить по линии ее действия в какую угодно другую точку, при этом действие силы не изменяется. Докажем это утверждение. Пусть на твердое тело действует сила Аксиома III. Равнодействующая двух сил, приложенных под углом в одной точке, проходит через ту же точку, равна по модулю и направлению диагонали параллелограмма, построенного на этих силах (рис.3). Как видно из рис.3, вектор Если известен угол a между силами
Равнодействующая сила Аксиома IV. Силы действия двух тел друг на друга равны по модулю и направлены по одной прямой в противоположные стороны. Таким образом, если одно тело действует на другое с силой F1, то второе тело также оказывает действие на первое с силой F2, причем F1 = F2 и
Опоры (связи) и их реакции Твердые тела условно разделяются на свободные и несвободные. Свободным называется тело, если оно из одного положения может быть перемещено в любом направлении (например, твердое тело, находящееся в воздухе или погруженное в жидкость); в противном случае оно называется несвободным (например, книга, лежащая на столе; груз, подвешенный на жестком тросе). Соседние тела, препятствующие перемещению несвободного твердого тела в каком-либо направлении, называются связями или опорами (для книги связью является стол, для груза - трос). Противодействие связей на несвободное твердое тело называется реакциями связей. Реакция, на основании аксиомы IV, должна быть равна и прямо противоположно направлена той силе, с которой несвободное тело оказывает действие на опору. Отбросив мысленно опоры и заменив их противодействие соответствующими силами, мы можем рассматривать сооружение или конструкцию как свободное тело, подверженное действию активных внешних сил (вес книги или груза) и сил пассивных - реакций связей. Сходящиеся силы Силы называются сходящимися, если линии их действия пересекаются в одной точке. Теорема о трех силах. Если на твердое тело действует уравновешенная система трех непараллельных сил, расположенных в одной плоскости, то линии действия этих сил пересекаются в одной точке. Доказательство. Пусть три непараллельные, взаимно уравновешенные силы расположены в одной плоскости. Точки их приложения А1, А2 и А3 (рис.12). Продолжим линии действия сил до пересечения в точке О. Согласно следствию из аксиомы II перенесем эти силы в точку О и заменим их согласно аксиоме III одной равнодействующей силой.
Так как силы Теорема о геометрическом сложении сходящихся сил. Система сходящихся сил имеет равнодействующую, равную их геометрической сумме. Доказательство. Пусть в точке О приложены силы `P1, `P2, `P3 (рис.14). Последовательно применяя правило параллелограмма сил, получим равнодействующую сил Затем найдем равнодействующую сил Равнодействующая всех четырех В случае n сходящихся сил их равнодействующая будет равна:
Равнодействующую силу `R можно найти путем построения силового многоугольника, являющегося замкнутой ломаной линией, звеньями которой служат сходящиеся силы данной системы (рис.15). Если система сходящихся сил уравновешена, то ее равнодействующая равна нулю.
Уравнения равновесия сходящихся сил. Если сходящиеся силы в прямоугольной системе координат X, Y, Z уравновешены, то равнодействующая сила обращается в нуль, и, соответственно равны нулю ее проекции на координатные оси
Если уравновешенная система сходящихся сил расположена в одной плоскости, то уравнение равновесия запишется в виде:
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 293. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
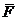 (точка А) (рис.1).
(точка А) (рис.1). Поскольку к телу может быть приложена не одна, а несколько сил, то их совокупность называется системой сил. Две системы сил, оказывающие одинаковое действие на тело, называются эквивалентными. Если под действием системы сил тело находится в равновесии, то данная система является взаимно уравновешенной, или статически эквивалентной нулю.
Поскольку к телу может быть приложена не одна, а несколько сил, то их совокупность называется системой сил. Две системы сил, оказывающие одинаковое действие на тело, называются эквивалентными. Если под действием системы сил тело находится в равновесии, то данная система является взаимно уравновешенной, или статически эквивалентной нулю.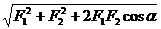 .
. и
и 
 +
+ 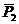
 должны уравновешиваться, то по аксиоме I
должны уравновешиваться, то по аксиоме I  и
и  .
. =
= 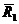 +
+ 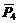 сил будет: R= =R2+ P4 =
сил будет: R= =R2+ P4 = 
 ;
;  ;
;  .
.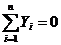 .
.