
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Математическое ожидание случайной величиныМатематическим ожиданиемили средним значением дискретной случайнойвеличины Х называется число
Если же дискретная случайнаявеличина Х имеет n возможных значений, то
Таким образом, математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на соответствующие вероятности этих значений. Математическим ожиданием непрерывной случайнойвеличины Х называется число
Если же возможные значения непрерывной случайнойвеличины Х принадлежат лишь отрезку [ a ;b], то Пример 12.Непрерывная случайная величина Х задана плотностью вероятности.
Найти М[X]. Решение.
Простейшие свойства математического ожидания. Свойство1. Математическое ожидание постоянной величины равно самой постоянной, то есть М[C]=С. Свойство2. Постоянный множитель можно выносить за знак математического ожидания, то есть М[СX]=СM[X].
Дисперсия и среднее квадратическое отклонение случайной величины Дисперсиейслучайной величины Х называется число, характеризующее степень разброса возможных значений случайной величины относительно ее математического ожидания, обозначаемое D[X] и равное D[X]=M[(X-M[X])2]. Следовательно, для дискретной случайнойвеличины D[X] находят по формуле
mx – математическое ожидание M[X]. Для непрерывной случайнойвеличины
Средним квадратическим отклонениемслучайной величины Х называется число σx = Среднее квадратическое отклонение σx также характеризует степень отклонения возможных значений случайной величины относительно ее mx, но имеет размерность случайной величины.  Простейшие свойства дисперсии. Свойство1. Дисперсия постояннойвеличины равна нулю. D[C]=0 Свойство2. Постоянный множительможно выносить за знак дисперсии, возводя его при этом в квадрат, т.е. D[СX]=С2D[X]. Свойство3. Dx=M[X2]-mx2.
Пример 13.Найти дисперсию случайной величины Х, имеющей следующий закон распределения
Решение. Воспользуемся формулой Dx=M[X2]-mx2. Найдем М[X]=(-3)·0,2+(-1)·0,5+2·0,3=-0,5; M[X2]=(-3)2·0,2+(-1)2·0,5+22·0,3=3,5; следовательно, Dx=3,5-(-0,5)2=3,5-0,25=3,25. Можно вычислить σx = Таблица соотношения начальной буквы фамилии студента и варианта контрольных заданий
ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ |
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 391. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

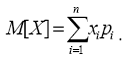






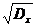 , где Dx=D[X].
, где Dx=D[X].
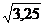 ≈ 1,80.
≈ 1,80.