
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Анализ и прогнозирование с помощью линейного уравнения множественной регрессииУравнение регрессии позволяет не только понять, как формируется значение результата Y под воздействием исследуемых факторов, но и дает возможность оценить степень влияния каждого из них на Y по отдельности. Как указывалось выше, коэффициент линейного уравнения регрессии bj показывает, на сколько единиц в среднем изменяется результат Y при изменении значения соответствующего фактора Xj на одну единицу и неизменных уровнях других факторов. Однако из-за различий единиц измерения факторов и степени их колеблимости сопоставить факторы по степени их влияния на результат Y только с помощью коэффициентов уравнения регрессии не всегда возможно. Для этой цели могут использоваться средние коэффициенты эластичности, бета–коэффициенты и дельта–коэффициенты. Средний коэффициент эластичности Ej показывает, на сколько процентов в среднем изменяется результат Y при изменении значения фактора Xj на один процент и фиксированных уровнях других факторов:
где Бета–коэффициент Bj показывает, на какую часть величины своего стандартного отклонения Sy в среднем изменяется результат Y при изменении фактора Xj на величину своего стандартного отклонения
где С помощью бета-коэффициентов можно проранжировать факторы по степени их влияния на результат Y: большая абсолютная величина бета-коэффициента соответствует более сильному влиянию фактора на Y. Квадрат бета–коэффициента является чистой мерой влияния вариации изолированного фактора на вариацию результата Y и показывает долю вариации результата Y, объясняемую только за счет вариации фактора Xj.  Дельта–коэффициентDj оценивает долю вклада фактора Xj в суммарное влияние на результат Y всех факторов, включенных в модель:
где Для правильно построенной модели все дельта-коэффициенты имеют положительные значения и их сумма равна 1. Это вытекает из равенства
При достаточно сильной межфакторной корреляции некоторые дельта-коэффициенты могут оказаться отрицательными вследствие того, что соответствующий коэффициент уравнения регрессии имеет знак, противоположный парному коэффициенту корреляции этого фактора с результатом Y. Интерпретация отрицательных дельта-коэффициентов лишена смысла, при этом искажаются выводы и по дельта-коэффициентам других факторов. Помимо целей анализа модель множественной регрессии может использоваться и для прогнозирования значений зависимой переменной Y при заданных значениях факторов. Также как и в случае парной регрессии рассчитанное по уравнению регрессии значение Y является случайной величиной. Стандартная ошибка прогноза фактического значениярезультата y0, в предположении того, что факторы X1, X2, …, Xp примут значения, задаваемые вектором
где Sрег — стандартная ошибка регрессии (3.17); Интервальный прогноз фактического значения результата y0 с доверительной вероятностью g имеет вид:
где tтаб — табличное значение t-критерия Стьюдента при уровне значимости |
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 465. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||
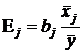 ,
,
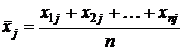 ,
, 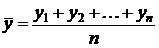 — средние значения фактора Xj и результата Y соответственно.
— средние значения фактора Xj и результата Y соответственно.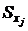 и неизменных значения других факторов:
и неизменных значения других факторов: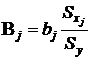 ,
,
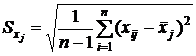 ;
; 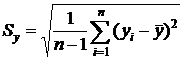 .
.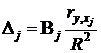 ,
,
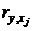 — коэффициент корреляции между фактором Xj и результатом Y; R2 — множественный коэффициент детерминации.
— коэффициент корреляции между фактором Xj и результатом Y; R2 — множественный коэффициент детерминации.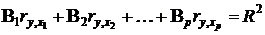 .
.
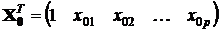 (матрица транспонирована для более компактной записи), определяется по любой из формул:
(матрица транспонирована для более компактной записи), определяется по любой из формул: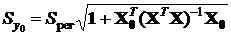 ;
;
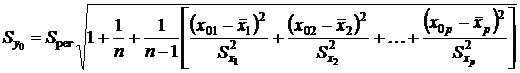 ,
,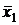 ,
, 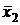 , …,
, …, 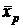 — средние значений факторов X1, X2, …, Xp соответственно;
— средние значений факторов X1, X2, …, Xp соответственно; 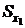 ,
, 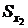 , …,
, …, 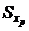 — стандартные отклонения факторов X1, X2, …, Xp.
— стандартные отклонения факторов X1, X2, …, Xp.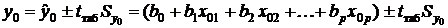 ,
,
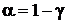 и числе степеней свободы
и числе степеней свободы 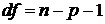 (см. приложение 3).
(см. приложение 3).