
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дослідимо гетероскедастичність на основі тесту Гольфельда—Квандта. ⇐ ПредыдущаяСтр 4 из 4 Алгоритм: 1. Вибираємо ту пояснювальну змінну, яка може викликати гетероскедастичність залишків. У даному випадку припусти- Сортуємо статистичну інформацію за змінною Х1 (інвестиції)
2. Визначимо параметр c зі співвідношення:
де n — кількість спостережень (n = 20); c — кількість спостережень, які необхідно в даному тесті відкинути всередині сукупності спостережень (c = 6). 3. Виділяємо дві сукупності спостережень (по сім спостережень) і за цими сукупностями будуємо економетричні моделі.
Скориставшись функцією «Лінійн» (програма Exсel), дістали такі результати для першої та другої сукупностей:
Сума квадратів залишків становить
4. Розраховуємо критерій R*
Порівняємо його з критичним значенням F-критерію для обраного рівня значущості (0,05) і ступеня свободи (n – c)/2 – m. R* = 0,213659; Fкрит = 9,276619. Оскільки R* < Fкрит (0,21 < 9,28), то інвестиції не викликають гетероскедастичність залишків, тобто зміна дисперсії залишків не може викликатися зміною цієї пояснювальної змінної. Тест Глейзера.На основі цього тесту визначається чиста та мішана гетероскедастичність. За цим тестом необхідно знайти залежність між модулем залишків та кожною пояснювальною змінною: 
У цій моделі перевіряється достовірність оцінок параметрів Побудуємо прості економетричні моделі модуля залишків залежно від кожної пояснювальної змінної:
(1,888) (–1,204)
(2,249) (–1,226)
(1,424) (–1,012) Перевіримо статистичну значущість оцінок параметрів кожної з цих моделей, застосувавши t-статистику. У дужках під оцінками параметрів моделей приведені фактичні значення t-критеріїв. Табличне значення цього критерію за рівня значущості a = 0,05 і ступеня свободи n – m = 18 дорівнює: t(0,05) крит = 2,10. Порівнюючи фактичні значення t-критеріїв з табличним, робимо висновок, що в другому рівнянні оцінка параметра a0 є статистично значущою. Отже, можна дійти висновку про наявність мішаної гетероскедастичності, яка викликається зміною тих пояснювальних змінних, які впливають на залежну змінну, але не включені до моделі. Щоб оцінити параметри моделі узагальненим методом найменших квадратів, необхідно сформувати матрицю S. Побудова матриці P, S, P–1, S–1.Оскільки ми маємо справу з мішаною гетероскедастичністю, то використовуємо третю гіпотезу щодо визначення lі:
Для розрахунку
бо в цій моделі оцінка параметра Підставивши в цю модель фактичні значення пояснювальної змінної Х2, дістанемо розрахункові залишки за модулем та квадрати цих залишків:
Значення вектора abs( Запишемо матрицю S, діагональні елементи якої визначаються за такою формулою: Оцінювання параметрів моделі методом Ейткена за допомогою матриці S–1. Оператор оцінювання запишеться у такому вигляді: Прогноз залежної змінної.Точковий прогноз за наявності гетероскедастичності має такий вигляд:
де
Запишемо вектор прогнозованих пояснювальних змінних:
Тоді прогнозне значення прибутку буде таке: Для того щоб знайти інтервальний прогноз прибутку, необхідно обчислити стандартну похибку прогнозу. Вона визначається за формулою:
Перейдемо від стандартної похибки прогнозу до граничної, яка подається у такому вигляді:
Додавши похибку до точкового прогнозу, дістанемо максимально можливе значення залежної змінної на перспективу, а віднявши — мінімальне значення:
Отже, прогнозне значення прибутку міститиметься в інтервалі:
АВТОКОРЕЛЯЦІЯ 8.1.1. Поняття автокореляції. Означення 8.1. Автокореляція — це наявність взаємозв’язку між послідовними елементами часового чи просторового ряду даних. В економетричних дослідженнях часто виникають такі ситуації, коли дисперсія залишків є сталою, але спостерігається їх коваріація. Це явище називають автокореляцією залишків. Автокореляція залишків найчастіше спостерігається тоді, коли економетрична модель будується на основі часових рядів. Якщо існує кореляція між послідовними значеннями деякої пояснювальної змінної, то буде спостерігатись і кореляція послідовних значень залишків. Автокореляція може бути також наслідком помилкової специфікації економетричної моделі, зокрема наявність автокореляції залишків може означати, що необхідно ввести до моделі нову незалежну змінну. У загальному випадку ми вводимо до моделі лише деякі з істотних змінних, а вплив змінних, яких виключено з моделі, має позначитися на зміні залишків. Існування кореляції між послідовними значеннями виключеної з розгляду змінної не обов’язково має викликати відповідну кореляцію залишків, бо вплив різних змінних може взаємно погашатися. Якщо кореляція послідовних значень виключених з моделі змінних спостерігається, то загроза виникнення автокореляції залишків стає реальністю. Проілюструємо проблему автокореляції залишків на прикладі простої економетричної моделі. Нехай де припускається, що залишки
причому
де Величина r є коефіцієнтом автокореляції залишків, що характеризує рівень взаємозв’язку кожного наступного значення з попереднім, тобто коваріацію залишків. Специфікація моделі (8.1) на відміну від моделей, які розглядались у розд. 7, має індекс t, що свідчить про її динамічний характер, тобто t — період часу, для якого будується така модель на основі динамічних (часових) рядів вихідних даних. Розглянемо залишки моделі ut, враховуючи (8.2):
Звідси де Оскільки Визначимо диперсію залишків ut.
Враховуючи, що послідовні значення
де Тоді Коваріація послідовних значень залишків запишеться у такому вигляді:
і в загальному випадку тобто для моделі (8.1) не задовольняється гіпотеза про незалежність послідовних значень залишків. Вираз (8.5) можна записати так:
Це означає, що за наявності автокореляції залишків друга необхідна умова подається у вигляді:
де S — матриця коефіцієнтів автокореляції s-го порядку для ряду
Якщо
то Порівнюючи матрицю, яку маємо в даному разі, з матрицею за наявності гетероскедастичності, побачимо, що вони істотно відрізняються одна від одної. Це пов’язано з тим, що природа порушення другої умови для застосування методу 1МНК для явищ гетероскедастичності та автокореляції різна. Отже, для гетероскедастичних залишків, розглянутих у розд. 7, існує одна форма порушення стандартної гіпотези, згідно з якою 8.1.2. Наслідки автокореляції залишків. Знехтувавши автокореляцією залишків і оцінивши параметри моделі 1МНК, дійдемо таких трьох основних наслідків. 1. Оцінки параметрів моделі можуть бути незміщеними, але неефективними, тобто вибіркові дисперсії вектора оцінок 2. Оскільки вибіркові дисперсії обчислюються не за уточненими формулами, то статистичні критерії t- і F-статистики, які знайдено для лінійної моделі, практично не можуть бути використані в дисперсійному аналізі при автокореляції. 3. Неефективність оцінок параметрів економетричної моделі призводить, як правило, до неефективних прогнозів, тобто прогнозів з доволі великою вибірковою дисперсією. Нагадаємо, що за відсутності автокореляції залишків матриця коваріацій для вектора оцінок Припустимо, що незалежні змінні і залишки можна подати у вигляді стаціонарних марковських процесів першого порядку:
Якщо коефіцієнти lіr додатні, то говорять про додатну автокореляцію. Від’ємна автокореляція в економетричних моделях спостерігається дуже рідко. Залишки
Із (8.10) бачимо, що зміщення Якщо додатна автокореляція спостерігається і в залишках, і в незалежній змінній, то 1МНК дає зміщення і для дисперсії залишків. Припустивши, як і раніше, що
Якщо r = l = 0,5 і n = 20, то 8.2. Перевірка наявності автокореляції 8.2.1. Критерій Дарбіна—Уотсона. Для перевірки наявності автокореляції залишків найчастіше застосовується критерій Дарбіна—Уотсона (DW): який може набувати значень із проміжку [0, 4]: Якщо залишки Коли DWфакт < DW1, залишки мають автокореляцію. Якщо Dwфакт > DW2, приймається гіпотеза про відсутність автокореляції. У разі DW1 <DW< DW2 конкретних висновків зробити не можна: необхідно далі провадити дослідження, збільшуючи сукупність спостережень. Зауважимо, що цей критерій призначений для малих вибіркових сукупностей. Вибірковий розподіл значень критерію Дарбіна—Уотсона залежить від емпіричних спостережень пояснювальних змінних і, якщо взяти до уваги цю обставину, можна стверджувати: параметр r для генеральної сукупності має тісний зв’язок з критерієм DW. Якщо r = 1, то значення DW = 0, при r = 0 DW = 2 і при r = –1 значення критерію DW = 4. Наведені співвідношення показують, що існують області, в яких застосування критерію Дарбіна—Уотсона не може дати певних результатів, про що вже було сказано. Верхні та нижні межі критерію DW визначають межі цієї області для різних розмірів вибірки, заданої кількості пояснювальних змінних та певного рівня значущості. Шкалу визначення наявності автокореляції на основі порівняння фактично розрахованого критерію Дарбіна—Уотсона та його критичних значень зображено на рис. 8.1.
Рис. 8.1. Шкала визначення наявності автокореляції Із рис. 8.1 випливає, що коли фактичне значення DW потрапляє в межі від нуля до нижньої критичної межі DW1, то гіпотезу про наявність автокореляції необхідно прийняти. Якщо фактичне значення критерію DW потрапляє в межі від верхнього критичного рівня DW2 до двох, то гіпотезу про наявність автокореляції потрібно відхилити. Коли фактичне значення критерію DW міститься в межах від нижнього до верхнього критичного значення, то існує невизначеність щодо наявності автокореляції залишків. У цьому випадку гіпотезу про наявність автокореляції доцільніше прийняти, ніж відхилити. Якщо фактичне значення критерію DW більше від 2, то, як було зазначено, може йтися про від’ємну автокореляцію. Оскільки критичні значення критерію DW табульовані для додатної автокореляції, то щоб зробити висновки стосовно від’ємної автокореляції, необхідно відняти розраховане значення критерію DW від 4 і цю різницю порівнювати з критичними значеннями критерію DW, як це було показано раніше.
üПриклад 8.1. Нехай обсяг вибірки складається з 20 спостережень. На основі цієї вибірки побудовано модель, яка включає в себе три пояснювальні змінні. Наведено табличні значення критерію Дарбіна — Уотсона DW1 і DW2 для 1 %- і 5 %-го рівнів значущості: DW1 DW2 a1 = 1 % 0,77 1,41 a2 = 5 % 1,00 1,68 Для додатної автокореляції залишків ці значення є межами п’яти інтервалів, за якими можна дійти таких висновків: 1) 0 £ DW £ 0,77— нульова гіпотеза відхиляється як з 1 %-м, так і за 5 %-м рівнями значущості; 2) 0,77 £ DW £ 1,00 — нульова гіпотеза відхиляється з 5 %-м рівнем значущості; для 1 %-го рівня значущості певних висновків зробити не можна; 3) 1,00 £ DW £ 1,41 — критерій не дає певних результатів як для одного, так і для другого рівня значущості; 4) 1,41 £ DW £ 1,68 — нульова гіпотеза не відхиляється з 1 %-м рівнем значущості, для 5 %-го рівня значущості певних висновків зробити не можна; 5) 1,68 £ DW £ 2,00 — нульова гіпотеза не відхиляється для обох рівнів значущості. Дж. Джонстон [2] наводить ряд спостережень, які свідчать про те, що верхній рівень DW2 ближчий до істинного значення прийняття гіпотези, яка перевіряється. Отже, якщо виникають сумніви, можна обмежитись одним показником — DW2. Це означає, що сам критерій також може мати зміщення, він указує на наявність серійної кореляції першого порядку і там, де її не повинно бути. Дж. Джонстон зауважує, що оскільки наслідки некоректного прийняття нульової гіпотези можуть бути набагато серйознішими, ніж її некоректного відхилення, то в сумнівних випадках нульову гіпотезу, як правило, краще відхилити. 8.2.2. Критерій фон Неймана. Для виявлення автокореляції залишків використовується також критерій фон Неймана: Звідси 8.2.3. Нециклічний коефіцієнт автокореляції. Цей коефіцієнт показує ступінь взаємозв’язку залишків кожного наступного значення з попереднім, а саме: 1-й ряд — 2-й ряд — Він обчислюється за формулою: Коефіцієнт 8.2.4. Циклічний коефіцієнт автокореляції. Він виражає ступінь взаємозв’язку рядів: 1-й ряд — 2-й ряд — Циклічний коефіцієнт обчислюється за формулою: Для досить довгих рядів вплив циклічних членів на значення коефіцієнта Фактично обчислене значення циклічного коефіцієнта автокореляції порівнюється з табличним для вибраного рівня значущості і довжини ряду n. Якщо
На практиці часто замість (8.16) обчислюють 8.3. Оцінвання параметрів моделі 8.3.1. Метод Ейткена. Нехай в економетричній моделі yt = a0 + a1xt + ut , (8.18) ut = де et — нормально розподілені випадкові залишки. Тоді, щоб усунути автокореляцію залишків ut, потрібно перетворити основну модель так, щоб вона мала нормально розподілені залишки et. Оскільки et = ut – rut – 1, то для такого перетворення запишемо модель для попереднього періоду yt – 1 = a0 + a1xt – 1 + ut – 1. (8.19) Помножимо ліву і праву частину її на У результаті дістанемо таку економетричну модель: yt – Оскільки в цій моделі (ut – Параметр r наближено можна знайти на основі залишків, якщо обчислити циклічний коефіцієнт кореляції r0. На практиці, як правило, r » r0, але r0 коригується на величину зміщення. Усі ці міркування покладено в основу методів оцінювання параметрів економетричної моделі з автокорельованими залишками. Для оцінювання параметрів економетричної моделі, що має автокореляцію залишків, можна застосувати узагальнений метод найменших квадратів (метод Ейткена), який базується на скоригованій вихідній інформації з урахуванням коваріації залишків. У розд. 7 було розглянуто метод Ейткена і показано, що система рівнянь для оцінювання параметрів моделі на основі цього методу записується так: або де
Y — вектор залежних змінних. Звідси
або
Отже, щоб оцінити параметри моделі за методом Ейткена, потрібно сформувати матрицю S або V. Матриця S має вигляд
У цій симетричній матриці Оскільки коваріація залишків Таку матрицю пропонується використовувати для оцінювання параметрів моделі з автокорельованими залишками за методом Ейткена. Покажемо, як розрахувати циклічний коефіцієнт кореляції.
або
де ut — величина залишків у період t; ut–1 — величина залишків у період t – 1; n — кількість спостережень. Якщо На практиці ρ = r0. Зауважимо, що параметр r0 має зміщення. Тому, використовуючи такий параметр для формування матриці S, можна скоригувати його на величину зміщення
де Матриця
де Дисперсія залишків з урахуванням зміщення обчислюється так:
Значення l можна обчислити методом 1МНК за допомогою авторегресійного рівняння xt = l xt–1 + vt. У такому разі за 1МНК
де xt взято як відхилення від свого середнього значення. Реалізація алгоритму Ейткена для оцінювання параметрів моделі включає такі п’ять кроків. Крок 1.Оцінювання параметрів моделі за методом 1МНК. Крок 2. Дослідження залишків на наявність автокореляції. Крок 3. Формування матриці коваріації залишків V або S. Крок 4. Обернення матриці V або S. Крок 5.Оцінювання параметрів методом Ейткена, тобто згідно з (8.21), (8.22).
üПриклад 8.2.За допомогою двох взаємозв’язаних часових рядів про роздрібний товарообіг та доходи населення побудувати економетричну модель, що характеризує залежність роздрібного товарообігу від доходу. Вихідні дані наведено в табл. 8.1.
Таблиця 8.1 Розв’язання 1. Ідентифікуємо змінні моделі: yt — роздрібний товарообіг у період t, залежна змінна; xt — дохід у період t, пояснювальна змінна. Звідси yt = f (xt , ut), де ut — стохастична складова, залишки. 2. Специфікуємо економетричну модель у лінійній формі: yt = a0 + a1xt + ut ;
ut = yt – 3. Визначаємо оцінки параметрів моделі
де
Економетрична модель має вигляд
4. Знаходимо розрахункові значення роздрібного товарообігу на основі моделі Таблиця 8.2 Записуємо оцінку критерію Дарбіна—Уотсона:
Порівнюємо значення критерію DW з табличним для a= 0,05 і n = 10. Критичні значення критерію DW у цьому разі такі: DW1 = 0,879 — нижня межа; DW2 = 1,320 — верхня межа. Оскільки критерій DWфакт < DW1, то можна стверджувати, що залишки ut мають додатну автокореляцію. Наявність чи відсутність автокореляції залишків можна також визначити за критерієм фон Неймана. Критерій фон Неймана 6. Застосовуюючи метод Ейткена, оцінюємо параметри економетричної моделі з автокорельованими залишками. Оператор оцінювання записуємо так:
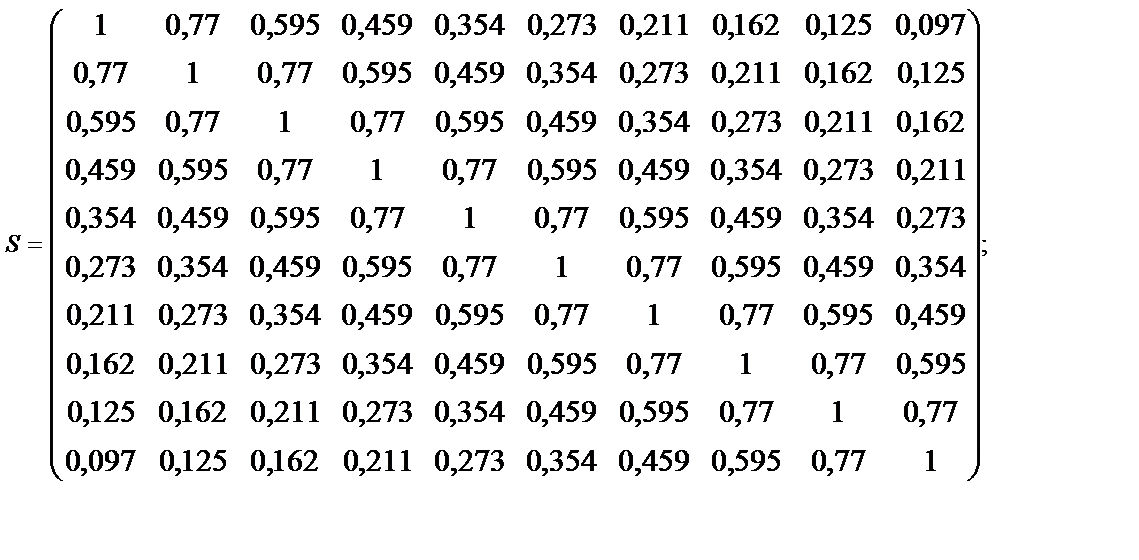
де Матриця S — матриця коваріацій залишків вигляду
7. Щоб сформувати матрицю S або V, необхідно визначити величину r, яка характеризує взаємозв’язок між послідовними членами ряду залишків. Нехай залишки описуються автокореляційною моделлю першого порядку ut = rut – 1+ et ,
Отже, матриця S набирає вигляду:
1); 2) 3) 4) 5)
Остаточно дістаємо економетричну модель:
8. Знайдемо розрахункові значення Таблиця 8.3 9. Обчислимо критерій Дарбіна—Уотсона і фон Неймана:
Порівнявши його з критичним значенням при n = 10 і a = 0,05, коли DWфакт< DW1, дійдемо висновку, що ми не звільнились від автокореляції залишків. Це означає, що вихідна гіпотеза, коли залишки описуються авторегресійною схемою першого порядку, не виконується. Якщо залишки описуються авторегресійною схемою вищого порядку, то доцільно виконати оцінювання параметрів моделі іншими методами, наприклад методом Кочрена—Оркатта або Дарбіна, які буде розгляну-
10. Визначаємо оцінку параметрів моделі, скориставшись оберненою матрицею S–1 вигляду:
Підставивши r = 0,77, дістанемо:
Вектор оцінок параметрів моделі:
Отже, Порівнюючи економетричні моделі (1) і (2), бачимо, що при оцінюванні параметрів методом Ейткена за допомогою матриці S–1, коли коваріація залишків для
8.4. Прогноз Теоретичні дослідження прогнозу в разі порушення умови (4.3) було розглянуто в розд. 7. Нехай маємо модель: Використаємо цю модель для визначення прогнозу залежної змінної
де
і W — вектор коваріації розрахованих залишків для n спостережень і прогнозних залишків un+1:
Якщо залишки описуються авторегресійною моделлю першого порядку, то з урахуванням рівності
Отже, вектор W можна дістати, помноживши Звідси Формула прогнозу має такий вигляд де üПриклад 8.5. Використовуючи економетричну модель, яку побудовано за даними про роздрібний товарообіг та дохід (приклад 8.2), визначити прогнозний рівень товарообігу, коли дохід становитиме xn+1= 55. Розв’язання 1. Запишемо співвідношення, яке визначатиме прогнозний рівень залежної змінної
де Хn+1 2. Скористаємося економетричною моделлю роздрібного товарообігу (приклад 8.2) для обчислення прогнозу:
3. Знайдемо оцінку залишків прогнозу
4. Визначимо точковий прогнозний рівень роздрібного товарообігу на одинадцятий рік (n + 1):
üПриклад 8.6. Виконаємо точковий та інтервальний прогноз прибутку на основі економетричної моделі, здобутої у прикладі 8.4. Спочатку задамо очікувані значення пояснювальних змінних:
точковий прогноз прибутку на основі моделі запишеться так:
Для визначення інтервального прогнозу розрахуємо стандартну похибку прогнозу за формулою:
Визначимо граничну похибку прогнозу за формулою:
Додавши граничну похибку до точкового прогнозу, дістанемо максимально можливий рівень прибутку:
Віднявши граничну похибку від точкового прогнозу, дістанемо мінімально можливий рівень прибутку:
У результаті маємо: Порівняємо отримані значення прогнозу прибутку зі значеннями прогнозу, здобутими на основі оцінок моделей за 1МНК:
Як бачимо, точковий та інтервальний прогнози прибутку на основі економетричних моделей, параметри яких оцінені 1МНК та УМНК, відрізняються в даному випадку несуттєво. Зауважимо, що оцінки за УМНК та кількісні характеристики, здобуті на основі цих оцінок, ніколи не будуть гіршими ніж за 1МНК.
6.5. Методи звільнення від мультиколінеарності Найпростіше позбутися мультиколінеарності в економетричній моделі можна, відкинувши одну зі змінних мультиколінеарної пари. Однак на практиці вилучення якогось чинника часто суперечить логіці економічних зв’язків. Позитивно впливає на звільнення від мультиколінеарності суттєве збільшення сукупності спостережень, але цей підхід не завжди можна реалізувати на практиці. Можна також перетворити певним чином пояснювальні змінні моделі: а) знайти відхилення від середньої; б) замість абсолютних значень змінних обчислити відносні (темпи зростання, приросту); в) нормалізувати пояснювальні змінні; г) використати «рідж-регресію». Розглянемо сутність «рідж-регресії» як одного з ефективних способів усунення мультиколінеарності. Згідно з теоремою Гаусса—Маркова оцінки — 1МНК є оцінками з найменшою середньоквадратичною похибкою серед усіх незміщених і лінійних щодо до Y оцінок. Але в економетрії доведено, що може існувати зміщена оцінка невідомих параметрів Доведено існування таких незміщених оцінок, для яких можна, змінюючи розмір сукупності спостережень, діставати багато значень зміщених лінійних оцінок — 1МНК ( Нехай надалі Δ визначає допустиму граничну похибку в оцінці істинного значення вектора А, тобто якщо Розглянемо щільності розподілу незміщених та зміщених оцінок параметрів моделі (рис. 6.1).
Рис. 6.1. Щільність розподілу незміщеної та зміщеної оцінок Згідно з рис. 6.1 можна зробити такі висновки: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 292. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,

 .
.
 .
. та
та 
 5,586 – 0,046x1;
5,586 – 0,046x1; 4,049 – 0,071x2;
4,049 – 0,071x2; 7,051 – 0,041x3.
7,051 – 0,041x3. .
. використаємо модель:
використаємо модель:
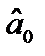 статистично значуща.
статистично значуща.

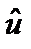 ) є діагональними елементами матриці P–1, а значення вектора (abs(
) є діагональними елементами матриці P–1, а значення вектора (abs(  — діагональними елементами матриці S–1.
— діагональними елементами матриці S–1. , де
, де 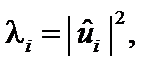

 ,
, — вектор оцінок параметрів моделі, здобутих методом Ейткена;
— вектор оцінок параметрів моделі, здобутих методом Ейткена; — останній діагональний елемент матриці Р–1 (1,409299);
— останній діагональний елемент матриці Р–1 (1,409299); — останній елемент залишків, здобутих методом 1МНК (0,624327).
— останній елемент залишків, здобутих методом 1МНК (0,624327). .
. .
.
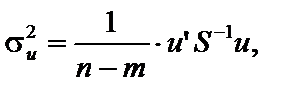

 ,
, ,
, ,
,
 .
.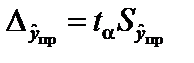 ,
, 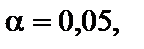


 61,531049,
61,531049, 58,595781.
58,595781.
 (8.1)
(8.1) задовольняють схему авторегресії першого порядку (стаціонарний марковський процес 1-го порядку), тобто залежать тільки від залишків попереднього періоду:
задовольняють схему авторегресії першого порядку (стаціонарний марковський процес 1-го порядку), тобто залежать тільки від залишків попереднього періоду: (8.2)
(8.2) , а для
, а для  виконуються такі властивості:
виконуються такі властивості:

 — номер зрушення (лагу) залишків щодо періоду t.
— номер зрушення (лагу) залишків щодо періоду t.
 (8.3)
(8.3) , то
, то 
 .
. незалежні, запишемо
незалежні, запишемо
 .
. . (8.4)
. (8.4)

 , (8.5)
, (8.5) . (8.6)
. (8.6) ,
, або
або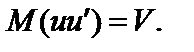
 ,
, . (8.7)
. (8.7) Для автокореляційних залишків ми стикаємося з іншою формою порушення цієї гіпотези.
Для автокореляційних залишків ми стикаємося з іншою формою порушення цієї гіпотези. . (8.8)
. (8.8) (8.9)
(8.9) і
і  взаємно незалежні, і їхні автокореляційні матриці діагональні, тобто вони не автокорельовані. Тоді можна показати, що звичайний метод найменших квадратів дає при достатньо великому n таку оцінку дисперсії параметрів
взаємно незалежні, і їхні автокореляційні матриці діагональні, тобто вони не автокорельовані. Тоді можна показати, що звичайний метод найменших квадратів дає при достатньо великому n таку оцінку дисперсії параметрів  . (8.10)
. (8.10) дисперсії оцінок параметрів тим більше, чим більші значення l і r (більша автокореляція). Нехай l= r = 0,5, тоді зміщення
дисперсії оцінок параметрів тим більше, чим більші значення l і r (більша автокореляція). Нехай l= r = 0,5, тоді зміщення  . Цей множник і буде загубленим при використанні 1МНК, що призводить до заниження дисперсії приблизно на 40 % порівняно з її справжнім значенням. Зі збільшенням l і r, наприклад, r = l = 0,8, зміщення буде
. Цей множник і буде загубленим при використанні 1МНК, що призводить до заниження дисперсії приблизно на 40 % порівняно з її справжнім значенням. Зі збільшенням l і r, наприклад, r = l = 0,8, зміщення буде 
 , тобто істинне значення дисперсії в чотири з половиною разу перевищуватиме те, яке дістали, застосувавши 1МНК.
, тобто істинне значення дисперсії в чотири з половиною разу перевищуватиме те, яке дістали, застосувавши 1МНК. і
і 
 . (8.11)
. (8.11) , тобто недооцінка дисперсії залишків становить близько 3,5 %, а при r = l = 0,8; n = 20 ця недооцінка дорівнюватиме приблизно 24,2 %.
, тобто недооцінка дисперсії залишків становить близько 3,5 %, а при r = l = 0,8; n = 20 ця недооцінка дорівнюватиме приблизно 24,2 %.  .
.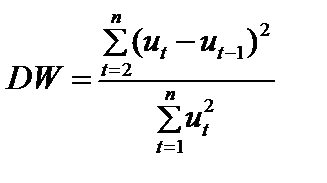 , (8.12)
, (8.12) .
.
 . (8.13)
. (8.13) . При
. При  Фактичне значення критерію фон Неймана порівнюється з табличним для вибраного рівня значущості і заданої кількості спостережень. Якщо
Фактичне значення критерію фон Неймана порівнюється з табличним для вибраного рівня значущості і заданої кількості спостережень. Якщо  , то існує додатна автокореляція, у протилежному випадку — вона відсутня.
, то існує додатна автокореляція, у протилежному випадку — вона відсутня. ;
; .
. . (8.14)
. (8.14) може набувати значень в інтервалі (–1; +1). Від’ємні значення його свідчать про від’ємну автокореляцію, додатні — про додатну. Значення, що містяться в деякій критичній області біля нуля, свідчать про відсутність автокореляції, тобто стверджують нульову гіпотезу про відсутність автокореляції залишків. Оскільки ймовірнісний розподіл
може набувати значень в інтервалі (–1; +1). Від’ємні значення його свідчать про від’ємну автокореляцію, додатні — про додатну. Значення, що містяться в деякій критичній області біля нуля, свідчать про відсутність автокореляції, тобто стверджують нульову гіпотезу про відсутність автокореляції залишків. Оскільки ймовірнісний розподіл 
 ,
,  ;
; ,
,  .
.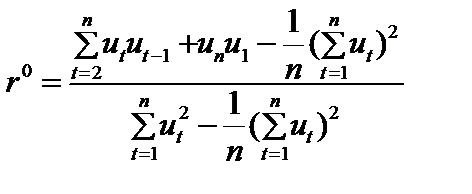 . (8.15)
. (8.15) неістотний, тому можна вважати, що ймовірнісний розподіл
неістотний, тому можна вважати, що ймовірнісний розподіл  , то існує автокореляція. Припускаючи, що
, то існує автокореляція. Припускаючи, що  , циклічний коефіцієнт автокореляції можна записати у вигляді
, циклічний коефіцієнт автокореляції можна записати у вигляді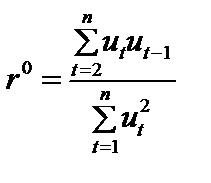 . (8.16)
. (8.16)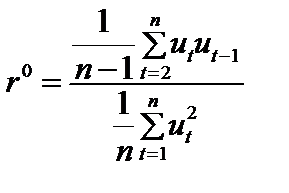 . (8.17)
. (8.17) ut + et ,
ut + et ,  ,
, та віднімемо від моделі для періоду t (8.18).
та віднімемо від моделі для періоду t (8.18). yt – 1 = a0(1–
yt – 1 = a0(1–  ) + a1(xt –
) + a1(xt –  xt – 1) + (ut –
xt – 1) + (ut –  ut – 1). (8.20)
ut – 1). (8.20) ut – 1) дорівнює et, то очевидно, що коли вихідні дані перетворені, а саме yt –
ut – 1) дорівнює et, то очевидно, що коли вихідні дані перетворені, а саме yt –  yt – 1, xt –
yt – 1, xt –  xt – 1, то для оцінювання параметрів можна застосувати 1МНК. При цьому для перетворення можна використати перші різниці yt – yt – 1 і xt – xt – 1, коли
xt – 1, то для оцінювання параметрів можна застосувати 1МНК. При цьому для перетворення можна використати перші різниці yt – yt – 1 і xt – xt – 1, коли  наближається до одиниці. Якщо
наближається до одиниці. Якщо  близьке до нуля, то вихідні дані можна не перетворювати. Зауважимо, що коли
близьке до нуля, то вихідні дані можна не перетворювати. Зауважимо, що коли  = 1, у перетвореній моделі буде відсутній вільний член (як виняток може бути ситуація, коли вихідна модель містить лінійний часовий тренд). Якщо залишки вихідної моделі характеризувались додатною автокореляцією, використання перших різниць може спричинити виникнення від’ємної автокореляції.
= 1, у перетвореній моделі буде відсутній вільний член (як виняток може бути ситуація, коли вихідна модель містить лінійний часовий тренд). Якщо залишки вихідної моделі характеризувались додатною автокореляцією, використання перших різниць може спричинити виникнення від’ємної автокореляції. (8.21)
(8.21) (8.22)
(8.22) — вектор оцінок параметрів економетричної моделі;
— вектор оцінок параметрів економетричної моделі; — матриця пояснювальних змінних;
— матриця пояснювальних змінних; — матриця, транспонована до матриці X;
— матриця, транспонована до матриці X;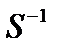 — матриця, обернена до матриці кореляції залишків;
— матриця, обернена до матриці кореляції залишків; — матриця, обернена до матриці V, де
— матриця, обернена до матриці V, де  а
а 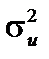 —
— 

 .
. виражає коефіцієнт автокореляції s-го порядку для залишків
виражає коефіцієнт автокореляції s-го порядку для залишків  при s>2 часто наближається до нуля, то матриця, обернена до матриці S, матиме такий вигляд:
при s>2 часто наближається до нуля, то матриця, обернена до матриці S, матиме такий вигляд: . (8.23)
. (8.23) ,
, ,
,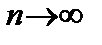 , то
, то  .
. ,
,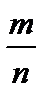 — величина зміщення (m — кількість змінних моделі).
— величина зміщення (m — кількість змінних моделі). , де
, де  — залишкова дисперсія, що визначається за формулою
— залишкова дисперсія, що визначається за формулою ,
, — вектор, транспонований до вектора залишків u; n – m — кількість ступенів свободи.
— вектор, транспонований до вектора залишків u; n – m — кількість ступенів свободи. .
. ,
, ;
; .
. ,
,  за методом найменших квадратів, припускаючи, що залишки ut не корельовані:
за методом найменших квадратів, припускаючи, що залишки ut не корельовані:
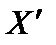 — матриця, транспонована до X.
— матриця, транспонована до X. ;
; ;
;  ;
; ;
; ;
;

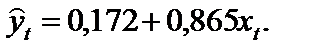
 і визначаємо залишки ut (табл. 8.2).
і визначаємо залишки ut (табл. 8.2). .
. Це значення порівнюється з табличним;
Це значення порівнюється з табличним;  при n=10 і рівні значущості
при n=10 і рівні значущості  = 0,05. Оскільки
= 0,05. Оскільки  , то існує додатна автокореляція залишків.
, то існує додатна автокореляція залишків.
 — матриця, обернена до матриці S;
— матриця, обернена до матриці S;  — матриця, обернена до матриці V.
— матриця, обернена до матриці V. ,
, .
. .
.

 ;
; ;
; ;
; ;
; ;
;  .
. (1)
(1)

 на основі побудованої економетричної моделі та визначимо залишки vt (табл. 8.3).
на основі побудованої економетричної моделі та визначимо залишки vt (табл. 8.3). .
. .
. .
.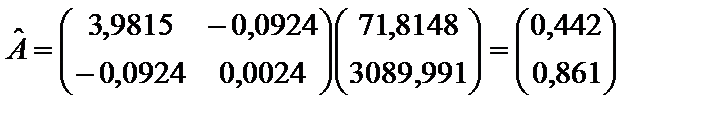 .
. ;
; 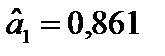 , і економетрична модель подається у вигляді
, і економетрична модель подається у вигляді . (2)
. (2)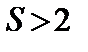 відсутня, дістаємо ті самі результати, що й раніше.
відсутня, дістаємо ті самі результати, що й раніше. де
де 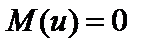 і
і  яка побудована для n спостережень.
яка побудована для n спостережень. для періоду n + 1,коли в цьому періоді задано незалежну змінну
для періоду n + 1,коли в цьому періоді задано незалежну змінну  . Формула дає найкращий незміщений прогноз:
. Формула дає найкращий незміщений прогноз:
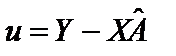
 .
. можна записати:
можна записати: .
. на останній стовпець матриці V. Але оскільки
на останній стовпець матриці V. Але оскільки  , то добуток
, то добуток  являє собою останній рядок матриці E, помножений на
являє собою останній рядок матриці E, помножений на  .
.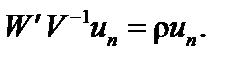
 (8.30)
(8.30)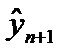 — прогнозний рівень залежної змінної;
— прогнозний рівень залежної змінної;  — прогнозне значення незалежної змінної.
— прогнозне значення незалежної змінної.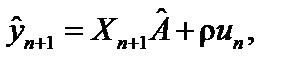
 — залишки прогнозу, а un — залишки періоду t(t = n), здобуті згідно з 1МНК.
— залишки прогнозу, а un — залишки періоду t(t = n), здобуті згідно з 1МНК. =0,442 + 0,861xn+1 = 0,442 + 0,861 55 = 0,442 + 47,35 = 47,8.
=0,442 + 0,861xn+1 = 0,442 + 0,861 55 = 0,442 + 47,35 = 47,8. , де r — коефіцієнт коваріації залишків;
, де r — коефіцієнт коваріації залишків;  — залишки за моделлю для t = 10.
— залишки за моделлю для t = 10.
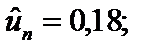

 = 47,8 + 0,14 = 47,94.
= 47,8 + 0,14 = 47,94. ;
; 



 .
.







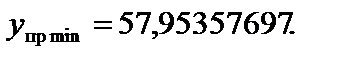
 ніж найкраща серед незміщених оцінок.
ніж найкраща серед незміщених оцінок. ) для кожної вибірки і для них будувати щільність розподілу —
) для кожної вибірки і для них будувати щільність розподілу —  . Аналогічно можна дістати множину незміщених оцінок
. Аналогічно можна дістати множину незміщених оцінок  і для них знайти щільність закону розподілу —
і для них знайти щільність закону розподілу —  .
. , то оцінка вважається незміщеною (якісною), а при
, то оцінка вважається незміщеною (якісною), а при  — навпаки.
— навпаки.