Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Похибки оцінок параметрів значно збільшуються, відповідно збільшуються їхні інтервали довіри.Адже стандартні похибки оцінок параметрів моделі обчислюються як корінь квадратний із дисперсій цих оцінок. Раніше ми показали, що дисперсії оцінок параметрів моделі значно збільшуються, а отже, стандартні та граничні похибки також збільшуються. Якщо
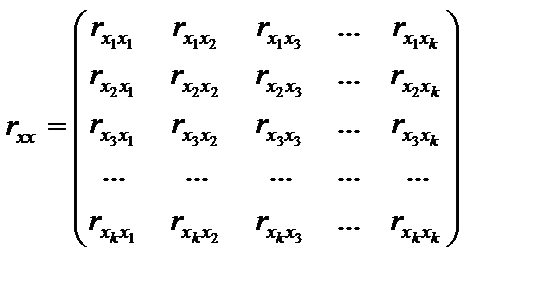
Це означає, що інтервал довіри за наявності мультиколінеарності буде в 2,29 разу більший, ніж тоді, коли її немає. 3. Оцінки параметрів моделі можуть бути статистично незначущими.Статистична незначущість оцінок параметрів моделі може виявлятись на фоні високого рівня довіри до моделі в цілому. Це пояснюється не тим, що досліджувані пояснювальні змінні мають слабкий зв’язок із залежною, а наявністю їхнього взаємозв’язку. Нагадаємо, що для оцінювання статистичної значущості оцінок параметрів моделі застосовуються t-критерії, в яких абсолютне значення оцінки порівнюється з її похибкою. Оскільки в разі мультиколінеарності похибки значно збільшуються і збільшується також їхня кореляція, то t-критерії прямуватимуть до нуля. Трапляються випадки, коли існує мультиколінеарність, але економетрична модель в цілому є достовірною, статистично значущими є всі оцінки параметрів моделі. Тоді мультиколінеарність не є проблемою. У цих випадках оцінки параметрів мають такі числові значення, які попри збільшення стандартних похибок залишаються набагато більшими і, відповідно, статистично значущими. На мультиколінеарність можна не зважати і тоді, коли мета економетричного моделювання — лише прогнозування. Чим вище R2, тим точніший прогноз, але ця закономірність справджується лише доти, доки залежні змінні, що прогнозуються, мають однакову майже лінійну залежність з початковою матрицею пояснювальних змінних X.  З огляду на перелічені наслідки мультиколінеарності при побудові економетричної моделі потрібно мати інформацію про те, що між пояснювальними змінними не існує мультиколінеарності. 6.3. Ознаки мультиколінеарності Коли серед парних коефіцієнтів кореляції пояснювальних змінних є такі, рівень яких наближається або дорівнює множинному коефіцієнту кореляції, то це означає можливість існування мультиколінеарності. Інформацію про парну кореляцію може дати симетрична матриця коефіцієнтів парної кореляції між пояснювальними змінними: Проте коли до моделі входять більш як дві пояснювальні змінні, то вивчення питання про мультиколінеарність не може обмежуватись інформацією, що її дає ця матриця. Явище мультиколінеарності в жодному разі не зводиться лише до існування парної кореляції між пояснювальними змінними. Більш загальна перевірка передбачає знаходження визначника (детермінанта) матриці rxx, який є детермінантом кореляції і позначається Якщо Коли коефіцієнт частинної детермінації Якщо в економетричній моделі знайдено мале значення оцінки параметра Якщо під час побудови економетричної моделі на основі покрокової регресії введення нової пояснювальної змінної істотно змінює оцінку параметрів моделі за незначного підвищення (або зниження) коефіцієнтів кореляції чи детермінації, то ця змінна перебуває, очевидно, у лінійній залежності від інших, що їх було введено до моделі раніше. Усі ці ознаки мультиколінеарності мають один спільний недолік: ні одна з них чітко не розмежовує випадки, коли залежність між пояснювальними змінними істотна і коли нею можна знехтувати.
6.4. Алгоритм Фаррара—Глобера Найповніше дослідити мультиколінеарність можна застосувавши алгоритм Фаррара—Глобера. Цей алгоритм має три види статистичних критеріїв, згідно з якими перевіряється мультиколінеарність усього масиву пояснювальних змінних ( Усі ці критерії при порівнянні з їхніми критичними значеннями дають змогу робити конкретні висновки щодо наявності чи відсутності мультиколінеарності пояснювальних змінних. Опишемо алгоритм Фаррара—Глобера. Крок 1. Нормалізація змінних. Позначимо вектори пояснювальних змінних економетричної моделі через 1) де Крок 2. Знаходження кореляційної матриці згідно з двома методами нормалізації змінних: 1) де Крок 3. Визначення критерію де Значення цього критерію порівнюється з табличним при Крок 4. Визначення оберненої матриці: Крок 5. Обчислення F-критеріїв: де Коефіцієнт детермінації для кожної змінної
Якщо коефіцієнт детермінації наближається до одиниці, то пояснювальна змінна мультиколінеарна з іншими. Крок 6. Знаходження частинних коефіцієнтів кореляції: де Крок 7. Обчислення t-критеріїв: Фактичні значення критеріїв Розглянемо застосування алгоритму Фаррара—Глобера до розв’язування конкретної задачі. Приклад 6.1. На середньомісячну заробітну плату впливає ряд чинників. Вирізнимо серед них продуктивність праці, фондомісткість та коефіцієнт плинності робочої сили. Щоб побудувати економетричну модель заробітної плати від згаданих чинників згідно з методом найменших квадратів, потрібно переконатися, що продуктивність праці, фондомісткість та коефіцієнт плинності робочої сили як незалежні змінні моделі — не мультиколеніарні. Вихідні дані наведені в табл. 6.1. Таблиця 6.1 Дослідити наведені чинники на наявність мультиколеніарністі. Розв’язання. Крок 1. Нормалізація змінних. Позначимо вектори незалежних змінних — продуктивності праці, фондомісткості, коефіцієнтів плинності робочої сили — через
де n — кількість спостережень, n = 10; m — число незалежних змінних, m = 3; Із формули бачимо, що спочатку потрібно обчислити середні арифметичні для кожної пояснювальної змінної:
Усі розрахункові дані для стандартизації змінних Таблиця 6.2 Дисперсії кожної незалежної змінної мають такі значення:
Тоді знаменник для стандартизації кожної незалежної змінної буде такий:
Матриця стандартизованих змінних подається у вигляді:
Крок 2. Знаходження кореляційної матриці:
де Ця матриця симетрична і має розмір 3 × 3. Для даної задачі
Кожний елемент цієї матриці характеризує тісноту зв’язку однієї незалежної змінної з іншою. Оскільки діагональні елементи характеризують тісноту зв’язку кожної незалежної з цією самою змінною, то вони дорівнюють одиниці. Зауважимо, що при знаходженні добутку матриць Інші елементи матриці r дорівнюють:
тобто вони є парними коефіцієнтами кореляції між пояснювальними змінними. Користуючись цими коефіцієнтами, можна зробити висновок, що між змінними Щоб відповісти на це запитання, потрібно ще раз звернутися до алгоритму Фаррара — Глобера і знайти статистичні критерії оцінки мультиколінеарності. Крок 3. Обчислимо детермінант кореляційної матриці r і критерій а) б) При ступені свободи Крок 4. Знайдемо матрицю, обернену до матриці r:
Крок 5. Використовуючи діагональні елементи матриці C,обчислимо F-критерії:
Для рівня значущості Оскільки F1факт < Fтабл; F2факт < Fтабл; F3факт < Fтабл, то ні одна з незалежних змінних не мультиколінеарна з двома іншими. Щоб визначити наявність попарної мультиколінеарності, продовжимо дослідження і перейдемо до кроку 6. Ї Крок 6. Обчислимо частинні коефіцієнти кореляції, скориставшись елементами матриці C:
Частинні коефіцієнти кореляції характеризують тісноту зв’язку між двома змінними за умови, що третя не впливає на цей зв’язок. Порівнявши частинні коефіцієнти кореляції з парними, які було наведено раніше, можна помітити, що частинні коефіцієнти значно менші за парні. Це ще раз показує, що на підставі парних коефіцієнтів кореляції не можна зробити висновків про наявність мультиколінеарності чи її відсутність. Крок 7. Визначимо t-критерій на основі частинних коефіцієнтів кореляції.
Табличне значення t-критерію при Отже, незважаючи на те, що між пояснювальними змінними досліджуваної моделі існує лінійна залежність, це не мультиколінеарність, тобто негативного впливу на кількісні оцінки параметрів економетричної моделі, не буде. Якщо F-критерій більший за табличне значення, тобто коли k-та змінна залежить від усіх інших у масиві, то необхідно вирішувати питання про її вилучення з переліку змінних. Якщо Найпростіше позбутися мультиколінеарності в економетричній моделі можна, відкинувши одну зі змінних мультиколінеарної пари. Але на практиці вилучення якогось чинника часто суперечить логіці економічних зв’язків. Тоді можна перетворити певним чином пояснювальні змінні моделі: а) взяти відхилення від середньої; б) замість абсолютних значень взяти відносні; в) стандартизувати пояснювальні змінні і т. iн. За наявності мультиколінеарності змінних потрібно звертати увагу й на специфікацію моделі. Іноді заміна однієї функції іншою, якщо це не суперечить апріорній інформації, дає змогу уникнути явища мультиколінеарності. Коли жодний з розглянутих способів не дає змоги позбутися мультиколінеарності, то параметри моделі слід оцінювати за методом головних компонентів.
üПриклад 6.2.(ЛАБ)На основі даних про чинники, що впливають на прибуток (табл. 6.3), дослідити їх на наявність мультиколінеарності за допомогою алгоритму Фаррара—Глобера, що містить три статистичні критерії: ü c2; ü F-критерій; ü t-критерій.
Розв’язання. Дослідимо наявність мультиколінеарності, виконавши такі кроки: 1. Нормалізацію (стандартизацію) пояснювальних змінних моделі. 2. Розрахунок кореляційної матриці rxx. 3. Визначення детермінанта матриці rxx. 4. Визначення критерію c2. 5. Розрахунок матриці, оберненої до матриці rxx. 6. Визначення F-критерію. 7. Обчислення частинних коефіцієнтів кореляції. 8. Визначення t-критерію. 1. Нормалізація (стандартизація) пояснювальних змінних моделі. Обчислимо середні арифметичні пояснювальних змінних:
Визначимо стандартні відхилення:
Нормалізуємо залежну та пояснювальні змінні:
2. Розрахунок кореляційної матриці нульового порядку.
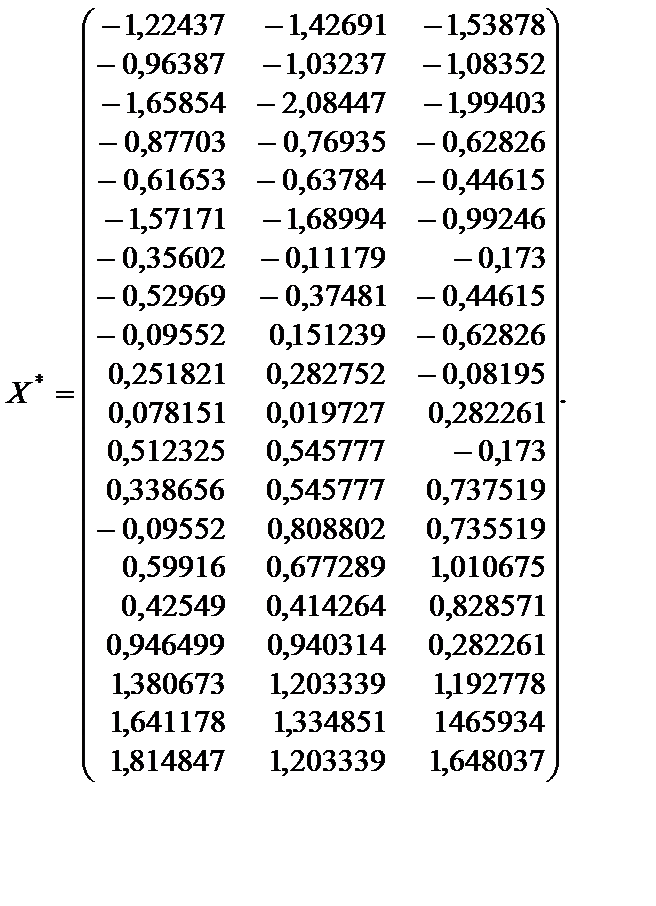
де X* — матриця нормалізованих пояснювальних змінних;
Маємо:
Парні коефіцієнти кореляції характеризують тісноту зв’язку між двома змінними. Вони можуть змінюватися в межах від – 1 до 1. У нашому випадку: r12 = 0,953; r13 = 0,912; r23 = 0,924. Ці коефіцієнти парної кореляції близькі до одиниці, тому можна передбачити, що всі досліджувані пояснювальні змінні є мультиколінеарними. 3. Визначення детермінанта матриці rxx: det r = 0,012257. Детермінант матриці rxx є точковою мірою мультиколінеарності, в нашому випадку він наближається до 0 (0,012257), а отже, мультиколінеарність існує. 4. Визначення критерію c2:
де n — кількість спостережень; m — кількість пояснювальних змінних. Виконавши обчислення, дістанемо:
Фактично обчислене значення критерію c2 порівнюємо з табличним за вибраного рівня значущості a і даних ступенів свободи: Доходимо висновку, що
Отже, 5. Розрахунок матриці, оберненої до матриці rхх:
Матриця с — симетрична, і її діагональні елементи завжди мають бути додатними. 6. Визначення F-критерію:
F1 = 92,43606; F2 = 107,3519; F3 = 54,5759; Fкрит. = 19,43704. Коли a = 0,05 і ступені свободи m – 1 = 2; n – m = 17, маємо Fкрит = 19,44. Фактично знайдене значення F-критерію порівнюємо з таб- У нашому випадку Fфакт > Fкрит, тобто пояснювальні змінні мультиколінеарні з рештою змінних. 7. Обчислення частинних коефіцієнтів кореляції:
r12.3 = 0,704215; r13.2 = 0.272309; r23.1 = 0,439721. Частинні коефіцієнти кореляції характеризують рівень тісноти зв’язку між двома змінними за умови, що решта змінних на цей зв’язок не впливає. Частинні коефіцієнти кореляції за модулем нижчі, ніж коефіцієнти парної кореляції, бо на їхній рівень не впливає решта змінних, які мають зв’язок із цими двома. 8. Визначення t-критерію:
tk1= 8,430911; tk2= 2,40553; tk3= 4,161543; tкрит = 2,109819. Обчислені t-критерії порівнюємо з табличним за вибраного рівня значущості a= 0,05 і ступенів свободи n – m = 17. Якщо tkj більше за tтабл, як у нашому випадку, то пара цих пояснювальних змінних тісно пов’язана між собою. Оскільки всі розраховані t-критерії більше від критичного, то між всіма пояснювальними змінними існує мультиколінеарність. А це означає, що метод найменших квадратів застосувати в цьому разі не можна.
ГЕТЕРОСКЕДАСТИЧНІСТЬ Припущення, які було зроблено під час оцінювання параметрів моделі 1МНК, на практиці можуть порушуватися. У розд. 6 було розглянуто проблему мультиколінеарності, яка пов’язана з порушенням четвертої умови.
Тепер розглянемо особливості економетричного моделювання, коли порушується умова (4.3), згідно з якою припускається, що відхилення мають такий розподіл імовірностей, який зберігається для всіх спостережень. Тоді дисперсія залишків лишається незмінною для кожного спостереження. Означення 7.1.Якщо дисперсія залишків стала для кожного спостереження, тобто Часто у практичних дослідженнях явище гомоскедастичності залишків порушується. Наприклад, будуючи економетричну модель, що характеризує залежність між заощадженнями і доходами населення на підставі теоретичної та практичної інформації, можна висунути гіпотезу, що дисперсія залишків за окремими групами населення змінюватиметься і буде пропорційною до середнього доходу цієї групи. Коли розглядати економетричну модель, що характеризує залежність між депозитними вкладами і розміром прибутку клієнтів банку або між витратами на харчування і доходом на одного члена сім’ї, витратами на харчування і загальними витратами, то також можна припустити, що дисперсія залишків для окремих груп спостережень змінюватиметься. У цих залежностях пояснювальна змінна може різко змінюватись, а динаміка залежної змінної буде досить помірною, не адекватною до зміни пояснювальної змінної. Це і приводить до зміни дисперсії залишків кожного спостереження або ж груп спостережень.Означення 7.2.Якщо дисперсія залишків змінюється для 7.2. Наслідки гетероскедастичності За наявності гетероскедастичності оцінки параметрів, отримані 1МНК, як правило, залишаються незміщеними, обґрунтованими, але неефективними. Нагадаємо, що дисперсія оцінок параметрів простої лінійної моделі визначається так:
У цих співвідношеннях дисперсія залишків є сталою, тому вона винесена за знак суми. За гетероскедастичності дисперсія Дисперсія оцінки Порівнюючи обидва співвідношення дисперсій оцінок Звідси інтервали довіри оцінок параметрів моделі також будуть більшими. Як наслідок, F та t-критерії дають неточні результати. Таким чином, якщо не звертати увагу на гетероскедастичність і використовувати звичайні процедури перевірки гіпотез, то висновки будуть неправильними, тобто потенційно гетероскедастичність є серйозною проблемою. Пояснимо сутність побудови моделі 1МНК за наявності гетероскедастичності. Припустимо, що дисперсія залишків змінюється пропорційно до величини Тоді, щоб усунути гетероскедастичність, можна перетворити вихідну інформацію, поділивши кожну зі змінних на xij і до цієї інформації застосувати 1МНК. Економетрична модель матиме вигляд: У результаті для оцінювання параметрів можна застосувати 1МНК. Зауважимо, що параметри а0 і а1 помінялися ролями. Вільним членом моделі замість а0 стала оцінка параметра а1. üПриклад 7.1. побудуємо економетричну модель, що характеризує залежність між заощадженнями та доходом населення, млрд ф. ст. (табл. 7.1). Таблиця 7.1 Скориставшись оператором оцінювання 1МНК
дістанемо Економетрична модель має такий вигляд: Коефіцієнт детермінації На перший погляд, результат наводить на думку, що специфікація моделі не містить похибки. Але логічно висунути гіпотезу, що відхилення заощаджень можуть бути пропорційними до доходу, тобто для цієї моделі досить ймовірне існування гетероскедастичності залишків. Отже, вихідну інформацію перетворимо, поділивши обидві змінні на дохід X (табл. 7.2):
Нове рівняння зв’язку згідно з даними табл. 7.2 має такий вигляд:
У результаті перетворення вихідних даних практично повністю змінилася специфікація моделі. Оскільки Виконавши цю процедуру, дістанемо таке: спостереження з меншими значеннями З наведеного прикладу бачимо, що явище гетероскедастичності не впливатиме на оцінки параметрів 1МНК, якщо певним чином перетворити вихідну інформацію. Згідно з цим, якщо економетрична модель має лише дві змінні, то це можна зробити так, як у прикладі 7.1. Це перетворення значно ускладнюється, якщо будується економетрична модель з багатьма змінними. У такому разі потрібно з’ясувати зміст гіпотези, згідно з якою 7.3. Методи визначення 7.3.1. Перевірка гетероскедастичності за крите- Крок 1. Вихідні дані залежної змінної Y розбиваються на k груп Крок 2. Закожною групою даних обчислюється сума квадратів відхилень:
Крок 3. Визначається сума квадратів відхилень у цілому по всій сукупності спостережень:
Крок 4. Обчислюється параметр
де n — загальна сукупність спостережень; nr — кількість спостережень r-ї групи. Крок 5. Обчислюється критерій:
який наближено відповідатиме розподілу
üПриклад 7.2. Для даних, які наведено у прикладі 7.1, перевіримо наявність гетероскедастичності згідно з критерієм m. Розв’язання Крок 1. Розіб’ємо дані залежної змінної, які наведені в таблиці 7.1, на три групи, по шість спостережень у кожній.
Крок 2. Обчислимо суму квадратів відхилень індивідуальних значень кожної групи від свого середнього значення: 2.1. 2.2.
Крок 3. Знайдемо суму квадратів відхилень за всіма трьома групами:
Крок 4. Обчислимо параметр
Крок 5. Знайдемо критерій
Цей критерій наближено задовольняє розподіл c2 з k – 1 = 2 ступенями свободи. Порівняємо значення критерію m з табличним значенням критерію c2 з k – 1 = 2 ступенями свободи за рівня довіри 0,99, 7.3.2. Параметричний тест Гольдфельда—Квандта. У випадку, коли сукупність спостережень невелика, розглянутий вище метод застосовувати недоцільно. У такому разі Гольдфельд і Квандт запропонували розглянути випадок, коли Y = XA + u. Для виявлення наявності гетероскедастичності згадані вчені склали параметричний тест, в якому потрібно виконати такі кроки. Крок 1. Упорядкувати спостереження відповідно до величини елементів вектора Xj. Крок 2. Відкинути c спостережень, які містяться в центрі вектора. Ця процедура дасть змогу порівняти дисперсії залишків для найменших та найбільших значень пояснювальної змінної. Згідно з експериментальними розрахунками автори знайшли оптимальні співвідношення між параметрами c і n для 30—60 спостережень, де n — кількість елементів вектора
Крок 3. Побудувати дві економетричні моделі на основі 1МНК за двома утвореними сукупностями спостережень обсягом Крок 4. Знайти суму квадратів залишків за першою (1) і другою (2) моделями
де
де Крок 5. Обчислити критерій
який у разі виконання гіпотези про гомоскедастичність відповідатиме F-розподілу з üПриклад 7.3. У табл. 7.3 наведено дані про загальні витрати та витрати на харчування сімей. Для цих даних перевірити гіпотезу про наявність гетероскедастичності.
Розв’язання. 1. Ідентифікуємо змінні: Y — вектор витрат на харчування, залежна змінна; X — вектор загальних витрат, незалежна змінна. Y = f (X, u). 2. Для перевірки гіпотези про наявність гетероскедастичності застосуємо параметричний тест Гольдфельда—Квандта. 2.1. Упорядкуємо значення незалежної змінної від меншого до більшого і відкинемо c значень, які містяться всередині впорядкованого ряду:
У результаті матимемо дві сукупності спостережень:
2.2. Побудуємо дві економетричні моделі на основі двох новостворених сукупностей спостережень. 2.3. Визначимо залишки за цими двома моделями:
Залишки та квадрати залишків наведено в табл. 7.3. 2.4. Обчислимо дисперсії залишків та знайдемо їх співвідношення:
2.5. Порівняємо критерій
7.3.4. Тест Глейзера. Ще один тест для перевірки гетероскедастичності запропонував Глейзер. Він розглядає регресію модуля залишків 1) 3) У цих рівняннях Рішення про відсутність гетероскедастичності залишків приймається на підставі статистичної значущості коефіцієнтів Можливі чотири випадки: 1) 2) 3) 4) У першому випадку залишки гетероскедастичні, причому існує чиста і мішана гетероскедастичність. У другому випадку залишки мають мішану гетероскедастичність. Третій випадок свідчить про наявність чистої гетероскедастичності. У четвертому випадку гетероскедастичність відсутня.
üПриклад 7.4. Нехай потрібно перевірити наявність гетероскедастичності для побудови економетричної моделі, яка описуватиме залежність між рівнем заощаджень і доходом. Вихідні дані наведено в табл. 7.4.
üПриклад 7.4. Нехай потрібно перевірити наявність гетероскедастичності для побудови економетричної моделі, яка описуватиме залежність між рівнем заощаджень і доходом. Вихідні дані наведено в табл. 7.4.
Таблиця 7.4 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 309. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
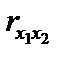 = 0,90, то похибка збільшиться в
= 0,90, то похибка збільшиться в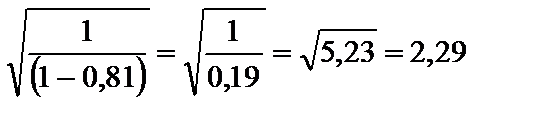 .
. . (6.6)
. (6.6)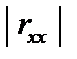 . Числові значення детермінанта кореляції задовільняють умову:
. Числові значення детермінанта кореляції задовільняють умову: 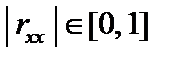 .
.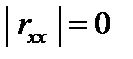 , то існує повна мультиколінеарність, а коли
, то існує повна мультиколінеарність, а коли 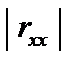 = 1, мультиколінеарність відсутня. чим ближче
= 1, мультиколінеарність відсутня. чим ближче 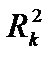 , який обчислено для регресійних залежностей між k-юпояснювальною змінною та рештою, має значення, близьке до одиниці, то можна говорити про наявність мультиколінеарності.
, який обчислено для регресійних залежностей між k-юпояснювальною змінною та рештою, має значення, близьке до одиниці, то можна говорити про наявність мультиколінеарності.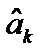 за високого рівня частинного коефіцієнта детермінації
за високого рівня частинного коефіцієнта детермінації 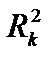 і водночас F-критерій істотно відрізняється від нуля, то це також може свідчити про наявність мультиколінеарності.
і водночас F-критерій істотно відрізняється від нуля, то це також може свідчити про наявність мультиколінеарності.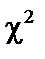 — «хі»-квадрат); кожної пояснювальної змінної з рештою змінних (F-критерій); кожної пари пояснювальних змінних (t-критерій).
— «хі»-квадрат); кожної пояснювальної змінної з рештою змінних (F-критерій); кожної пари пояснювальних змінних (t-критерій).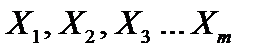 . Елементи нормалізованих векторів обчислимо за формулами:
. Елементи нормалізованих векторів обчислимо за формулами: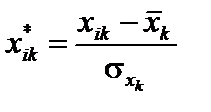 ; 2)
; 2) 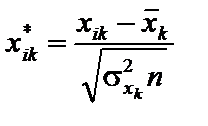 , (6.7)
, (6.7)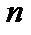 — кількість спостережень
— кількість спостережень 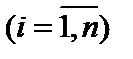 ;
; 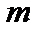 — кількість пояснювальних змінних
— кількість пояснювальних змінних 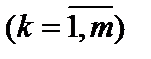 ;
; 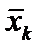 — середнє арифметичне k-ї пояснювальної змінної;
— середнє арифметичне k-ї пояснювальної змінної; 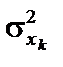 — дисперсія k-ї пояснювальної змінної.
— дисперсія k-ї пояснювальної змінної.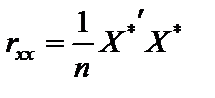 ; 2)
; 2) 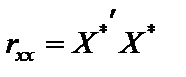 , (6.8)
, (6.8)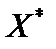 — матриця нормалізованих незалежних (пояснювальних) змінних,
— матриця нормалізованих незалежних (пояснювальних) змінних, 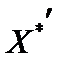 — матриця, транспонована до матриці
— матриця, транспонована до матриці 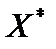 .
.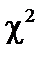 («хі»-квадрат):
(«хі»-квадрат):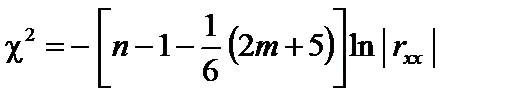 , (6.9)
, (6.9)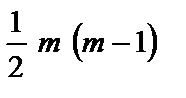 ступенях свободи і рівні значущості
ступенях свободи і рівні значущості 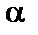 . Якщо
. Якщо 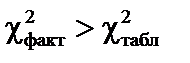 , то в масиві пояснювальних змінних існує мультиколінеарність.
, то в масиві пояснювальних змінних існує мультиколінеарність.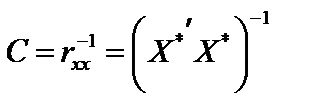 . (6.10)
. (6.10)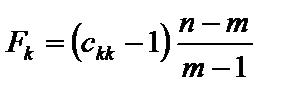 , (6.11)
, (6.11)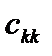 — діагональні елементи матриці C. Фактичні значення критеріїв порівнюються з табличними при m – 1 і n – m ступенях свободи і рівні значущості a. Якщо Fk факт > Fтабл, то відповідна k-та пояснювальна змінна мультиколінеарна з іншими.
— діагональні елементи матриці C. Фактичні значення критеріїв порівнюються з табличними при m – 1 і n – m ступенях свободи і рівні значущості a. Якщо Fk факт > Fтабл, то відповідна k-та пояснювальна змінна мультиколінеарна з іншими.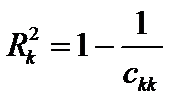 . (6.12)
. (6.12)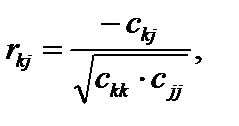 (6.13)
(6.13)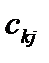 — елемент матриці C, що міститься в k-му рядку і j-му стовпці;
— елемент матриці C, що міститься в k-му рядку і j-му стовпці; 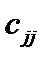 — діагональні елементи матриці C.
— діагональні елементи матриці C.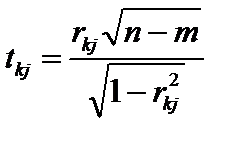 . (6.14)
. (6.14)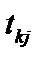 порівнюються з табличними при
порівнюються з табличними при 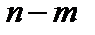 ступенях свободи і рівні значущості
ступенях свободи і рівні значущості 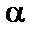 . Якщо tkj > tтабл, то між пояснювальними змінними
. Якщо tkj > tтабл, то між пояснювальними змінними 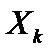 і
і 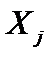 існує мультиколінеарність.
існує мультиколінеарність.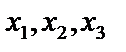 . Елементи стандартизованих векторів обчислимо за формулою:
. Елементи стандартизованих векторів обчислимо за формулою: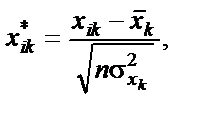
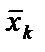 — середнє арифметичне значення вектора
— середнє арифметичне значення вектора 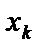 ;
; 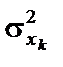 — дисперсія змінної
— дисперсія змінної 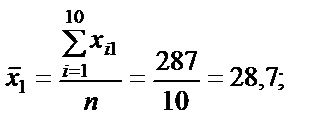
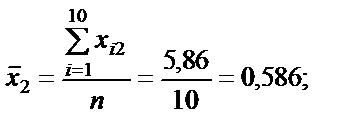
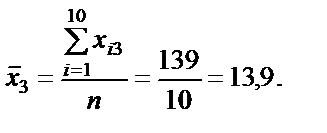
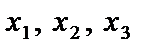 згідно з поданими співвідношеннями наведено в табл. 6.2.
згідно з поданими співвідношеннями наведено в табл. 6.2.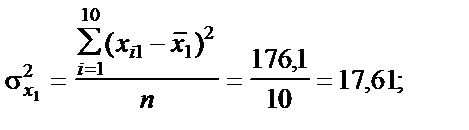
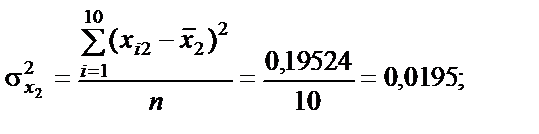
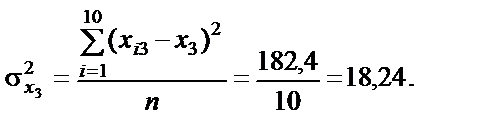
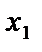 :
: 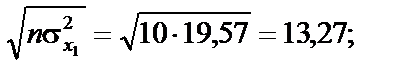
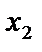 :
: 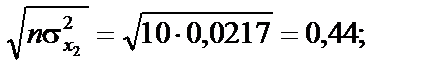
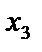 :
: 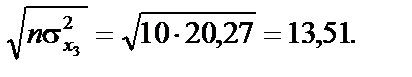
 .
.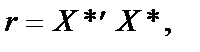
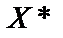 — матриця, транспонована до
— матриця, транспонована до 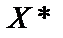 .
.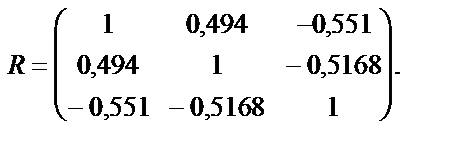
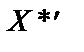
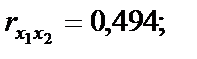
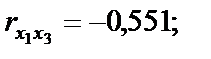
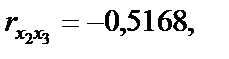
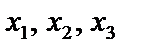 існує зв’язок. Але чи можна стверджувати, що цей зв’язок є виявленням мультиколінеарності, а через це негативно впливатиме на оцінку економетричної моделі?
існує зв’язок. Але чи можна стверджувати, що цей зв’язок є виявленням мультиколінеарності, а через це негативно впливатиме на оцінку економетричної моделі?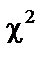 :
: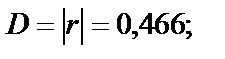
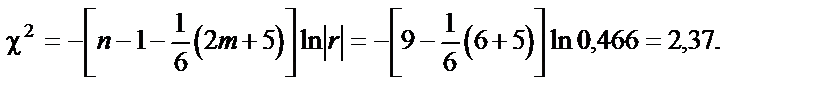
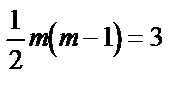 і рівні значущості
і рівні значущості 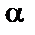 = 0,01 критерій
= 0,01 критерій 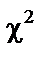 табл = 11,34. оскільки
табл = 11,34. оскільки 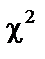 табл, доходимо висновку, що в масиві змінних не існує мультиколінеарності.
табл, доходимо висновку, що в масиві змінних не існує мультиколінеарності.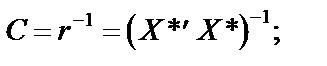
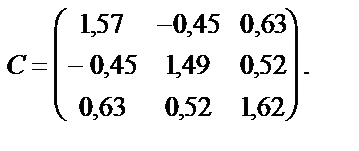
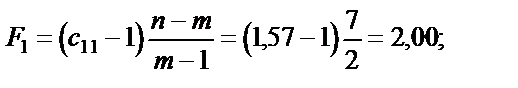
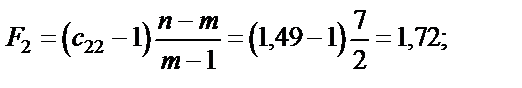
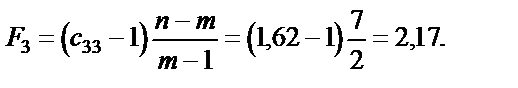
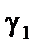 = 7 і
= 7 і 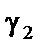 = 2 критичне (табличне) значення критерію F = 4,74.
= 2 критичне (табличне) значення критерію F = 4,74.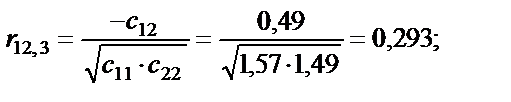
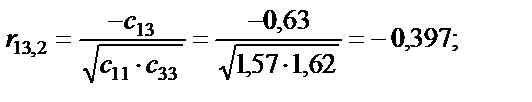
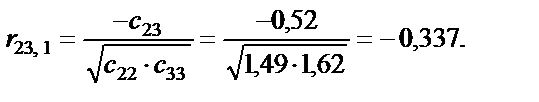
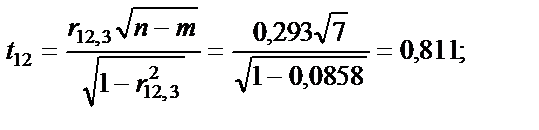
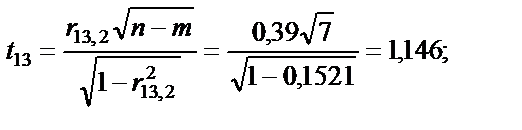
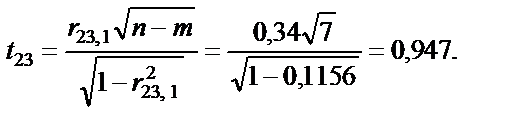
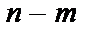 = 7 ступенях свободи і рівні значущості a = 0,05 дорівнює 1,69. Усі числові значення t-критеріїв, знайдених для кожної пари змінних, менші за їх табличні значення. Звідси робимо висновок, що всі пари незалежних змінних не є мультиколінеарними.
= 7 ступенях свободи і рівні значущості a = 0,05 дорівнює 1,69. Усі числові значення t-критеріїв, знайдених для кожної пари змінних, менші за їх табличні значення. Звідси робимо висновок, що всі пари незалежних змінних не є мультиколінеарними.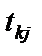 — критерій більший за табличний, то ці дві змінні (
— критерій більший за табличний, то ці дві змінні ( 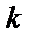 і
і 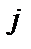 ) тісно пов’язані одною з одною. Звідси, аналізуючи рівень обох видів критеріїв
) тісно пов’язані одною з одною. Звідси, аналізуючи рівень обох видів критеріїв 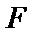 і
і 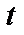 , можна зробити обгрунтований висновок про те, яку зі змінних необхідно вилучити з дослідження або замінити іншою. Проте заміна масиву незалежних змінних завжди має узгоджуватись з економічною доцільністю, що випливає з мети дослідження.
, можна зробити обгрунтований висновок про те, яку зі змінних необхідно вилучити з дослідження або замінити іншою. Проте заміна масиву незалежних змінних завжди має узгоджуватись з економічною доцільністю, що випливає з мети дослідження.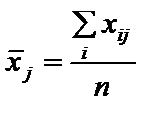 ,
, 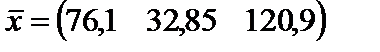 .
.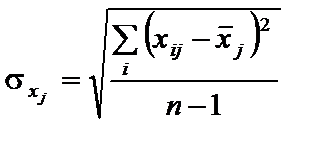 ,
, 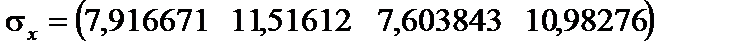 .
.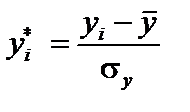 ;
; 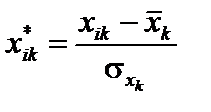 ;
;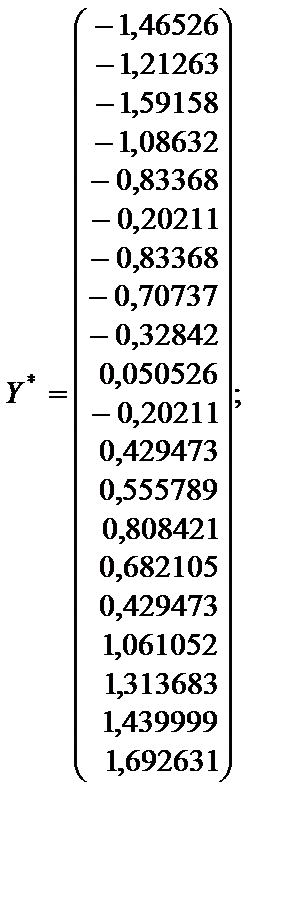
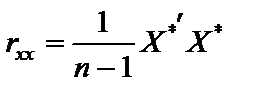 ,
,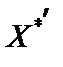 — матриця, транспонована до X*.
— матриця, транспонована до X*. .
.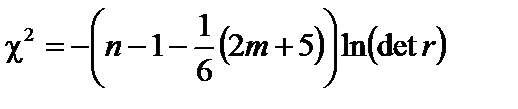 ,
,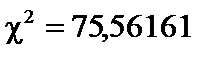 ;
; 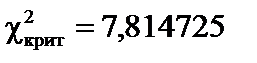 ; при
; при 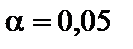 .
.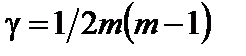 .
.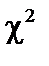 >
> 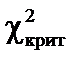 .
.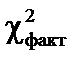 більше за
більше за 
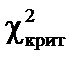 , а це означає, що в масиві пояснювальних змінних існує мультиколінеарний зв’язок, саме це і простежується в нашому випадку.
, а це означає, що в масиві пояснювальних змінних існує мультиколінеарний зв’язок, саме це і простежується в нашому випадку.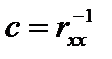 ;
;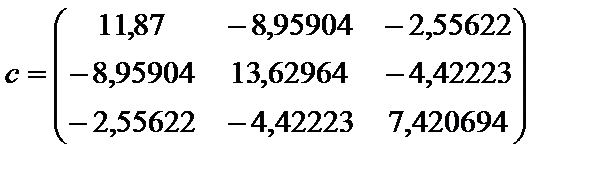 .
.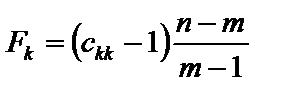 ;
; 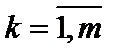 ;
;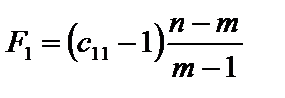 ;
; 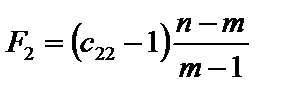 ;
; 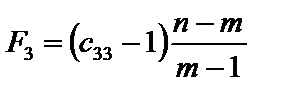 ;
;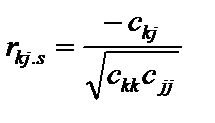 ;
;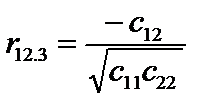 ;
; 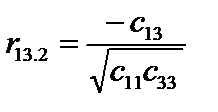 ;
; 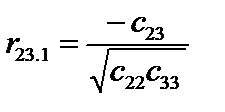 .
.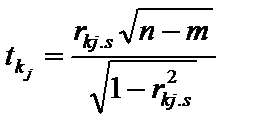 ;
;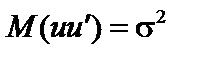 , то ця її властивість називається гомоскедастичністю.
, то ця її властивість називається гомоскедастичністю.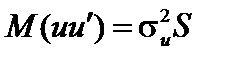 , то це явище називається гетероскедастичністю.
, то це явище називається гетероскедастичністю.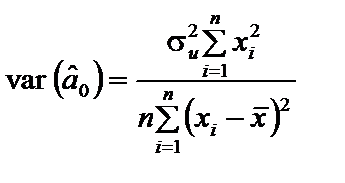 ; (7.1)
; (7.1)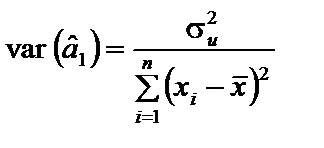 . (7.2)
. (7.2)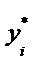
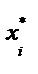
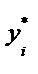
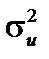 буде змінюватись через зростаючий розкид значень залишків, тобто вона зростатиме. Це означає, що буде зростати дисперсія оцінок параметрів моделі, яка приводить до збільшення їхніх стандартних похибок.
буде змінюватись через зростаючий розкид значень залишків, тобто вона зростатиме. Це означає, що буде зростати дисперсія оцінок параметрів моделі, яка приводить до збільшення їхніх стандартних похибок.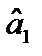 у разі гетероскедастичності запишеться так:
у разі гетероскедастичності запишеться так: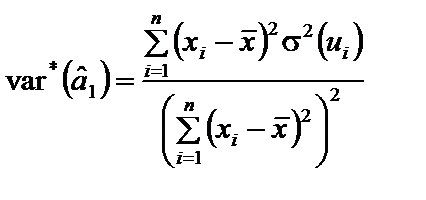 . (7.3)
. (7.3)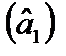 , бачимо, що
, бачимо, що 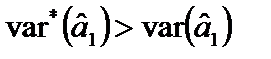 , тобто дисперсія оцінки параметра
, тобто дисперсія оцінки параметра 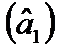 за гетероскедастичності більша, ніж дисперсія цієї оцінки за гомоскедастичності.
за гетероскедастичності більша, ніж дисперсія цієї оцінки за гомоскедастичності.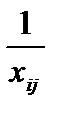 , де xij — i-те значення j-ї пояснювальної змінної, яка може викликати гетероскедастичність.
, де xij — i-те значення j-ї пояснювальної змінної, яка може викликати гетероскедастичність.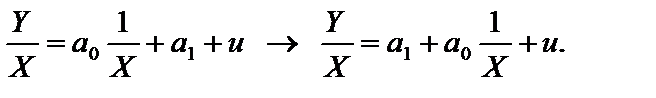 (7.4)
(7.4)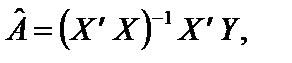
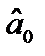 = –1,081;
= –1,081; 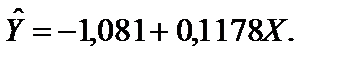
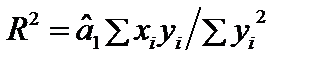 для цієї моделі
для цієї моделі 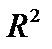 = 0,918, а це означає, що варіація заощаджень Y на 91,8 % визначається варіацією доходів населення.
= 0,918, а це означає, що варіація заощаджень Y на 91,8 % визначається варіацією доходів населення.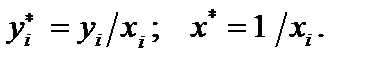
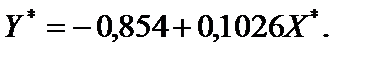
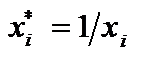 , то цей зв’язок нелінійний. По-друге,
, то цей зв’язок нелінійний. По-друге, 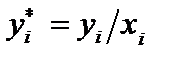 характеризує відносний показник — рівень заощаджень, який припадає на одиницю доходу.
характеризує відносний показник — рівень заощаджень, який припадає на одиницю доходу.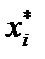 мають відносно більшу питому вагу при оцінюванні параметрів моделі, ніж у першому варіанті.
мають відносно більшу питому вагу при оцінюванні параметрів моделі, ніж у першому варіанті.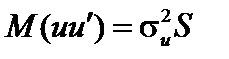 , де
, де 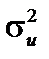 лишається невідомим параметром, а
лишається невідомим параметром, а 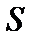 — відома симетрична додатно визначена матриця.
— відома симетрична додатно визначена матриця.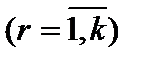 відповідно до зміни рівня величини Y.
відповідно до зміни рівня величини Y.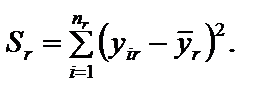
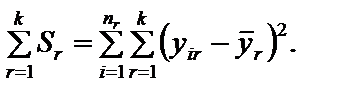
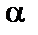 :
: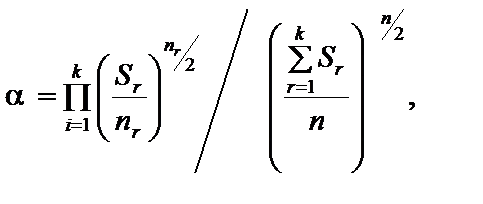
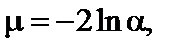 (7.5)
(7.5)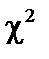 при ступені свободи
при ступені свободи 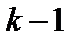 , коли дисперсія всіх спостережень однорідна. Тобто якщо значення
, коли дисперсія всіх спостережень однорідна. Тобто якщо значення 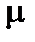 не менше за табличне значення
не менше за табличне значення 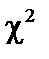 за вибраного рівня довіри і ступені свободи
за вибраного рівня довіри і ступені свободи 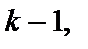 то спостерігається гетероскедастичність.
то спостерігається гетероскедастичність.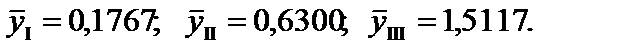
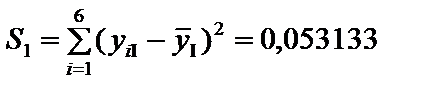 ;
; 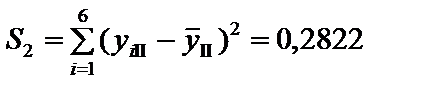 ;
;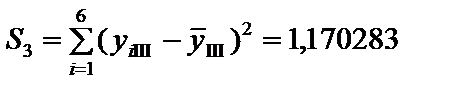 .
.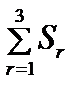 = S1 + S2 + S3 = 0,05313 + + 0,2822 + 1,1703 = 1,5056 .
= S1 + S2 + S3 = 0,05313 + + 0,2822 + 1,1703 = 1,5056 .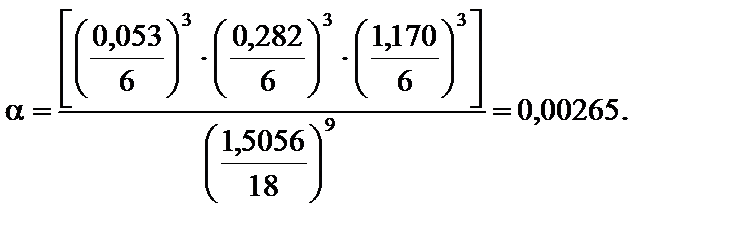
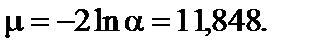
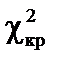 = 9,21. Оскільки m >
= 9,21. Оскільки m > 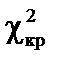 , то дисперсія залишків буде змінюватись, тобто для даних табл. 7.1 спостерігається гетероскедастичність.
, то дисперсія залишків буде змінюватись, тобто для даних табл. 7.1 спостерігається гетероскедастичність.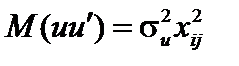 , тобто дисперсія залишків зростає пропорційно до квадрата однієї з незалежних змінних моделі:
, тобто дисперсія залишків зростає пропорційно до квадрата однієї з незалежних змінних моделі: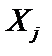 :
: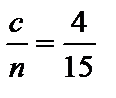 .
.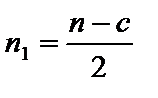 ,
, 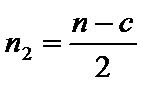 за умови, що обсяг
за умови, що обсяг 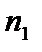 і
і 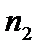 перевищує кількість змінних m. Якщо
перевищує кількість змінних m. Якщо 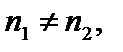 то відкидається перше або останнє спостереження сукупності.
то відкидається перше або останнє спостереження сукупності.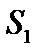 і
і 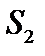 :
: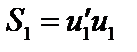 ,
,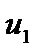 — залишки за моделлю (1);
— залишки за моделлю (1);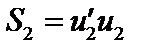 ,
,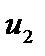 — залишки за моделлю (2).
— залишки за моделлю (2).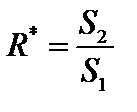 , (7.6)
, (7.6)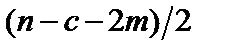 ,
, 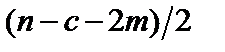 ступенями свободи. Це означає, що обчислене значення R* порівнюється з табличним значенням F-критерію для ступенів свободи
ступенями свободи. Це означає, що обчислене значення R* порівнюється з табличним значенням F-критерію для ступенів свободи 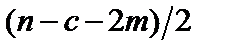 і
і 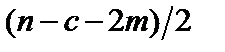 і вибраним рівнем значущості a. Якщо
і вибраним рівнем значущості a. Якщо 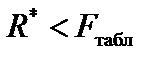 , то гетероскедастичність відсутня.
, то гетероскедастичність відсутня.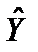
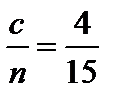 , c »4.
, c »4.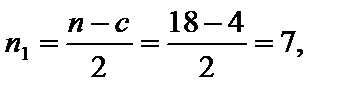
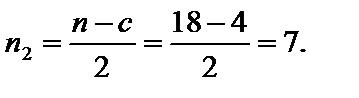
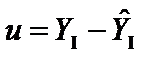 ;
; 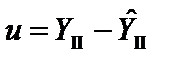 .
.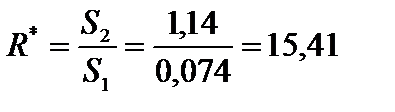 .
.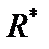 з критичним значенням F-критерію при g1= 5 і g2= 5 ступенях свободи і значущості a = 0,01 F(a= 0,01) = 11. Оскільки
з критичним значенням F-критерію при g1= 5 і g2= 5 ступенях свободи і значущості a = 0,01 F(a= 0,01) = 11. Оскільки 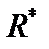 >
> 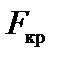 , то вихідні дані з імовірністю 0,99 мають гетероскедастичність.
, то вихідні дані з імовірністю 0,99 мають гетероскедастичність.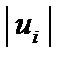 , що відповідають регресії найменших квадратів, як певну функцію від
, що відповідають регресії найменших квадратів, як певну функцію від 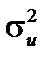 . Для цього використовуються такі види функцій:
. Для цього використовуються такі види функцій: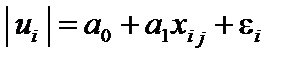 ;2)
;2) 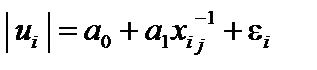 ;
;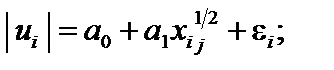 4)
4) 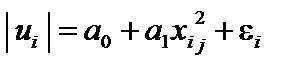 .
.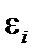 — стохастична складова.
— стохастична складова.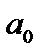 і
і 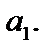 Переваги цього тесту визначаються можливістю розрізняти випадок чистої і мішаної гетероскедастичності.
Переваги цього тесту визначаються можливістю розрізняти випадок чистої і мішаної гетероскедастичності.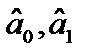 є статистично значущими;
є статистично значущими;