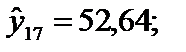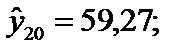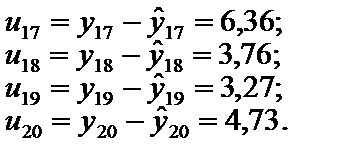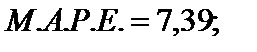Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Економетрична модель, що будується на основі системи рівнянь, крім регресійних функцій, може містити тотожності.Стр 1 из 4Следующая ⇒ Побудова будь-якої економетричної моделі, незалежно від того, на якому рівні і для яких показників вона будується, здійснюється як послідовність певних кроків. Крок 1. Знайомство з економічною теорією, висунення гіпотези взаємозв’язку. Чітка постановка задачі. Крок 2. Специфікація моделі. Використовуючи всі ті види функцій, які можуть бути застосовані для вивчення взаємозв’язків, необхідно сформулювати теоретичні уявлення і прийняті гіпотези у вигляді математичних рівнянь. Ці рівняння встановлюють зв’язки між основними визначальними змінними, припускаючи, що решта змінних є випадковими. Крок 3. Формування масивів вихідної інформації згідно з метою та завданнями дослідження. Крок 4. Оцінка параметрів економетричної моделі методом найменших квадратів. Аналіз залишків дає змогу відповісти на запитання: чи не суперечить специфікація моделі застосуванню 1МНК. Крок 5. Якщо деякі передумови застосування 1МНК не виконуються, то для подальшого аналізу треба замінювати специфікацію або застосовувати інші методи оцінювання параметрів. Крок 6. Верифікація моделі та її оцінок параметрів. Крок 7. Прогноз на основі моделі. Схематично всі кроки можна зобразити так:
4.2. Специфікація моделі Економетрична модель базується на єдності двох аспектів — теоретичного, якісного аналізу взаємозв’язків та емпіричної інформації. Теоретична інформація знаходить своє відображення у специфікації моделі. Специфікація моделі — це аналітична форма економетричної моделі на основі досліджуваних чинників. Вона складається з певного виду функції чи функцій, що використовуються для побудови моделей, має ймовірнісні характеристики, які притаманні стохастичним залишкам моделі.  З досвіду економетричних досліджень, а також на підставі якісного теоретичного аналізу взаємозв’язків між економічними показниками, можна навести клас функцій, які можуть описувати ці взаємозв’язки: 1) лінійна функція:
2) степенева функція:
3) гіпербола:
де 4) квадратична функція:
де У цих функціях: y — залежна (пояснювана) змінна;
Серед наведених видів функцій три останні є нелінійними. Але за допомогою перетворення залежної і незалежних змінних ці функції можна звести до лінійного виду. Лінійні функції найпоширеніші в економетричному моделюванні, тому обґрунтування економетричних методів розглянемо на базі лінійних моделей. Маючи на увазі, що вибір аналітичної форми економетричної моделі не може розглядатись без конкретного переліку незалежних змінних, специфікація моделі передбачає добір чинників для економетричного дослідження. При цьому в процесі такого дослідження можна кілька разів повертатись до етапу специфікації моделі, уточнюючи перелік незалежних змінних та вид функції, що застосовується. Адже коли вид функції та її складові не відповідають реальним процесам, то йдеться про похибки специфікації. Похибки специфікації моделі можуть бути трьох видів: 1) ігнорування при побудові економетричної моделі істотної пояснювальної змінної; 2) введення в модель незалежної змінної, яка не є істотною для вимірюваного зв’язку; 3) використання не відповідних математичних форм залежності. Перша з цих помилок призводить до зміщення оцінок, причому зміщення буде тим більшим, чим більша кореляція між введеними та не введеними до моделі змінними, а напрям зміщення залежить від знака оцінок параметрів при введених змінних і від характеру кореляції між введеними та навіть не введеними змінними. Оцінки параметрів також будуть зміщеними (в цьому випадку вони вищі), тому застосування способів перевірки їх значущості може призвести до хибних висновків щодо значень параметрів генеральної сукупності. Для відшукання цього джерела помилок специфікації досить важко запропонувати будь-які загальні міркування, оскільки незалежна змінна, що не враховується (або незалежні змінні), може бути одним із багатьох можливих пояснень. Про необхідність введення до моделі цих незалежних змінних можна лише здогадуватись на підставі апріорних міркувань. Проте відомі й більш формалізовані процедури, які дають змогу з’ясувати, наскільки істотним є введення до моделі будь-якої змінної. Так, наприклад, якщо побудувати економетричну модель на базі покрокової регресії (метод покрокової регресії розглянемо пізніше), то можна досить чітко ранжувати пояснювальні змінні за величиною їх впливу на залежну змінну. Про відсутність основної змінної свідчить зміна поведінки випадкового відхилення у помилково специфікованій моделі. Друга помилка специфікації. У випадку, коли до моделі вводиться змінна, яка неістотно впливає на залежну змінну, то (на відміну від першої помилки специфікації) оцінки параметрів моделі будуть незміщеними. При цьому за допомогою звичайних процедур можна дістати також незміщені оцінки дисперсій цих параметрів. Проте це не означає, що економетричну модель можна беззастережно розширювати за рахунок «неістотних» змінних. Адже існує ненульова ймовірність того, що в результаті використання вибіркових даних змінна, яка зовсім не стосується моделі, покаже істотний зв’язок із залежною змінною. А це означає, що кількісний зв’язок між змінними буде виміряно неправильно. Третя помилка специфікації. Припускається, що залежна змінна є лінійною функцією від деякої пояснювальної змінної, а насправді йдеться про квадратичну, кубічну чи якусь поліноміальну залежність вищого порядку. У цьому разі наслідки такі самі, як і за першої помилки специфікації: оцінки параметрів моделі матимуть зміщення. Питання про вибір найкращої форми залежності має базуватися на перевірці ступеня узгодженості виду функції з вихідними даними спостережень. Адекватність побудованої моделі можна встановити, проаналізувавши залишки моделі. Вони обчислюються як різниця між фактичними значеннями залежної змінної і розрахованими за моделлю. Щоб перевірити, чи має розподіл залишків невипадковий характер, можна скористатися критерієм Дарбіна—Уотсона. Тоді перевірка моделі на існування автокореляції першого порядку аналогічна перевірці того, наскільки вдало вибрано форму економетричної моделі. 4.3. Передумови застосування методу Нехай економетрична модель у матричній формі має вигляд
де Y — вектор значень залежної змінної; X — матриця пояснювальних змінних розміром Застосовуємо 1МНК для оцінювання параметрів моделі, якщо виконуються наведені далі умови. 1) Математичне сподівання залишків дорівнює нулю:
2) значення ui вектора залишків u незалежні між собою і мають сталу дисперсію:
3) пояснювальні змінні моделі не пов’язані із залишками: 4) пояснювальні змінні моделі утворюють лінійно незалежну систему векторів, або, іншими словами, пояснювальні змінні не повинні бути мультиколінеарними, тобто матриця Х має повний ранг. Перша умова, здавалося б, є очевидною. Адже коли математичне сподівання залишків не дорівнює нулю, то це означає, що існує систематичний вплив на залежну змінну і до модельної специфікації не введено всіх основних пояснювальних змінних. Якщо ця передумова не виконується, то йдеться про помилку специфікації. Друга умова передбачає наявність сталої дисперсії залишків та відсутність кореляції між ними. Наявність сталої дисперсії називають гомоскедастичністю. Проте вона може виконуватись лише тоді, коли залишки u є похибками вимірювання. Якщо залишки акумулюють загальний вплив змінних, які не враховано в моделі, то звичайно дисперсія залишків не може бути сталою величиною, вона змінюється для окремих груп спостережень. У такому разі йдеться про явище гетероскедастичності, яке впливає на методи оцінювання параметрів. Якщо між залишками існує залежність (автокореляція), то вона також впливає на методи оцінювання параметрів. Третя умова передбачає незалежність між залишками і пояснювальними змінними, яка порушується насамперед тоді, коли економетрична модель будується на базі одночасних структурних рівнянь або має лагові змінні. Тоді для оцінювання параметрів моделі використовується, як правило, дво- або трикроковий методи найменших квадратів. Четверта умоваозначає, що всі пояснювальні змінні, які входять до економетричної моделі, мають бути незалежними між собою. Проте очевидно, що в економіці дуже важко вирізнити такий масив пояснювальних змінних, які були б зовсім не пов’язані між собою. Тоді щоразу необхідно з’ясовувати, чи не впливатиме залежність пояснювальних змінних на оцінку параметрів моделі. Це явище називають мультиколінеарністюзмінних, що призводить до ненадійності оцінки параметрів моделі, підвищує їхню чутливість до вибраної специфікації моделі та до конкретного набору даних. Знижується рівень довіри до результатів верифікації моделей за допомогою 1МНК. Отже, це явище з усіх поглядів є, звичайно, небажаним. Але воно досить поширене, тому методи виявлення мультиколінеарності й способи її врахування за допомогою специфікації моделі чи спеціальних методів оцінювання параметрів є важливою економетричною проблемою.
4.4. Оператор оцінювання 1МНК Оцінимо методом 1МНК параметри моделі (4.1), для якої виконуються чотири розглянуті щойно умови. Рівняння (4.1) подамо у вигляді:
Продиференціюємо цю умову за
або X¢ — матриця, транспонована щодо матриці пояснювальних змінних X. Звідси Рівняння (4.6) дає матричну форму запису системи нормальних рівнянь, а формула (4.7) показує, що вектор Формули (4.6) і (4.7) можна дістати й інакше. Так, помноживши рівняння (4.1) зліва спочатку на
Оскільки
Згідно з (4.4), коли Неважко показати, що оцінки Â, обчислені за (4.7), мінімізують суму квадратів залишків u. Згідно з цим значення вектора Â є розв’язком системи нормальних рівнянь
Якщо незалежні змінні в матриці X взяті як відхилення кожного значення від свого середнього, то матрицю У цьому разі числа, розміщені на її головній діагоналі, характеризують величину дисперсій незалежних змінних, інші елементи відповідають взаємним коваріаціям. Отже, структура матриці моментів відбиває зв’язки між пояснювальними змінними. Чим ближчі показники коваріацій до значень дисперсій, тим ближчий визначник матриці Розглянемо приклад оцінювання параметрів моделі 1МНК.
üПриклад 4.1. Оцінити параметри економетричної моделі, що характеризує залежність між тижневими витратами на харчування, загальними витратами та розміром сім’ї. Вихідні дані наведено в табл. 4.1. Розв’язання. Запишемо економетричну модель:
де Y, X1 — загальні витрати; X2 — розмір сім’ї; u — залишки;
Таблиця 4.1 Оператор оцінювання параметрів моделі за 1МНК має вигляд:
де
Матриця X крім двох векторів незалежних змінних містить вектор одиниць. Він дописується в цій матриці ліворуч тоді, коли економетрична модель має вільний член. не дописуючи вектора одиниць, вільний член можна обчислити, скориставшись рівністю:
де Згідно з оператором оцінювання знайдемо:
Отже, економетрична модель має вигляд
Знайдені методом 1МНК оцінки параметрів такі:
Тобто, коли за всіх однакових умов незалежна змінна
4.5. Властивості оцінок параметрів Оцінки параметрів 1) незміщеності; 3) ефективності; 2) обґрунтованості; 4) інваріантності. Означення 4.2.Вибіркова оцінка
Застосовуючи оператор математичного сподівання до (4.7), дістаємо:
Оскільки за першою умовою Незміщеність — це мінімальна вимога, яка ставиться до оцінок параметрів Різниця між математичним сподіванням оцінки і значенням оціненого параметра називається зміщенням оцінки. Не можна плутати похибку оцінки з її зміщенням. Похибка дорівнює Другою важливою властивістю оцінки є її обґрунтованість. Означення 4.3.Вибіркова оцінка Іншими словами, оцінка обґрунтована, коли вона базується на законі великих чисел. Обґрунтованість оцінки означає, що чим більші будуються вибірки, тим більша ймовірність того, що похибка оцінки не перевищуватиме достатньо малого значення e. Для обґрунтованості оцінок, здобутих на основі 1МНК
де Q— додатно визначена матриця. Третя властивість оцінок Â — ефективність — пов’язана зі значенням дисперсії оцінок. Тут доречно сформулювати важливу теорему Гаусса—Маркова, що стосується ефективності оцінки 1МНК. · Теорема Гаусса—Маркова.Функція оцінювання за методом 1МНК покомпонентно мінімізує дисперсію всіх лінійних незміщених функцій вектора оцінок
де Отже, функція оцінювання 1МНК З означення дисперсії випливає, що
üПриклад 4.2. Визначити кількісну залежність між прибутком фірми і основними видами ресурсів, які вона вкладає у свою господарську діяльність: · інвестиції; · основні виробничі фонди; · фонд робочого часу. Для побудови економетричної моделі використаємо статистичну інформацію, що наведена в табл. 4.2. Таблиця 4.2
1. Ідентифікуємо змінні моделі. Y — вектор прибутку, залежна або пояснювана змінна; X1 — вектор інвестицій (незалежна або пояснювальна змінна); X2 — вектор основних виробничих фондів, незалежна або пояснювальна змінна; X3 — вектор фонду робочого часу (незалежна або пояснювальна змінна). 2. Специфікуємо економетричну модель. У лінійній формі: Y = a0 + a1X1 +a2X2 + a3X3 + u; у степеневій формі:
У цих функціях aj, u — стохастична або випадкова складова, яка визначає вплив усіх випадкових чинників на прибуток. Подамо степеневу функцію в лінійно-логарифмічній формі: LnY = lna0 + a1lnX1 + a2lnX2 + a3lnX3 + lnu. Запишемо розрахункові економетричні моделі на основі заданої статистичної інформації:
У цих розрахункових моделях Вектор стохастичної складової визначається як різниця між векторами фактичного і розрахункового прибутку залежної змінної (надалі послуговуватимемося терміном «залишки»):
3. Оцінимо параметри цих економетричних моделей методом найменших квадратів, матричний оператор якого Запишемо матрицю пояснювальних змінних: Транспонуємо матрицю Х:
Виконавши множення матриць
Знайдемо матрицю, обернену до
Помножимо X´Y: Запишемо вектор
Отже, дістанемо економетричну модель прибутку в лінійній формі:
Для побудови степеневої форми моделі прологарифмуємо вихідні дані: Скориставшись функцією програми «Exсel» «ЛИНЕЙН», знайдемо оцінки параметрів:
Отже, економетрична модель прибутку у степеневій формі набирає вигляду Як бачимо, економетрична модель прибутку в лінійній формі відрізняється від моделі у степеневій формі. Ця різниця полягає передусім у тому, що оцінки параметрів в обох моделях мають різний економічний зміст. У лінійній моделі оцінки параметрів У степеневій моделі оцінки параметрів Зміну напряму взаємозв’язку між прибутком та основними виробничими фондами у степеневій моделі можна пояснити особливостями статистичної інформації (можлива мультиколінеарність, автокореляція, про які йтиметься далі).
4.6. Коваріаційна матриця оцінок За допомогою коваріаційної матриці розраховуються основні показники випадкового розсіювання оцінок У класичній регресійній моделі Y = XA + u;вектор Відомо, що для характеристики випадкових змінних
Оцінки коваріаційної матриці На головній діагоналі матриці Отже,
де Зауважимо, що матриця коваріації оцінок параметрів моделі характеризує також ступінь їх випадкового розсіювання, який обчислюється, як значення детермінанта коваріаційної матриці cov(A). Детермінант коваріаційної матриці
Часто використовується й інша характеристика цього випадкового розсіювання значень багатовимірної випадкової величини — слід коваріаційної матриці tr:
Виходячи із додатної визначеності матриці Ступінь тісноти взаємозв’язку між окремими оцінками параметрів моделі
Усе це говорить про те, що коваріаційна матриця вектора оцінок параметрів моделей містить досить важливу інформацію про їхню якість. Незміщена оцінка дисперсії залишків розраховується так:
де n — кількість спостережень; m — кількість змінних у моделі. Оскільки вектор залишків
Звідси маємо альтернативну форму запису дисперсії залишків:
Позначимо (k, j)-й елемент матриці Коваріації
üПриклад 4.3. Для економетричної моделі Y = 8,8 + 0,2Х1 + + 6,97Х2 + u, (приклад 4.1) обчислимо коваріаційну матрицю Отже, маємо:
n = 16; m = 2. Розв’язання. 1. Обчислимо незміщену оцінку дисперсії залишків
2. Визначимо дисперсії оцінок
3. Обчислимо коваріації відповідних оцінок параметрів:
Знак «мінус» перед оцінками коваріацій Отже, дістанемо дисперсійно-коваріаційну матрицю
4. Запишемо стандартні похибки оцінок параметрів моделі:
Стандартні похибки характеризують середні лінійні коливання оцінок параметрів моделі навколо свого математичного сподівання. Чим менші ці похибки, тим стійкіші оцінки параметрів моделі. Остаточні висновки стосовно стійкості оцінок можна зробити лише тоді, коли порівняти її з абсолютними значеннями оцінок параметрів моделі. Порівняємо кожну стандартну похибку
Отже, стандартні похибки оцінок параметрів щодо рівня самих оцінок становлять відповідно 52,8 %, 23 % і 15 %, а це свідчить про зміщеність оцінок. Це означає, що залишки можуть мати систематичну складову, яка зумовлюється неточною специфікацією моделі. Наприклад, не всі основні чинники, що впливають на тижневі витрати, пов’язані з харчуванням (скажімо, ціни на продукти харчування) внесено до моделі.
4.7. Прогноз залежної змінної. Економетричне моделювання зв’язку між економічними показниками завжди складаєтьмя з трьох етапів: побудови економетричної моделі;перевірки статистичної значущості моделі та оцінювання її параметрів; прогнозування на основі моделі. Використаємо модель (4.1) для знаходження прогнозного значення y0, яке відповідатиме очікуваним значенням матриці незалежних змінних X0. Розглянемо спочатку точковий прогноз і припустимо, що ми визначили його як деяку лінійну функцію від yi:
де і — номер спостереження ( Оскільки де Х0 — матриця очікуваних значень пояснювальних змінних. Задаючи X0, підставимо значення цього вектора в побудовану економетричну модель
Щоб дістати інтервальний прогноз, необхідно розрахувати середню похибку прогнозу. Вона зростає з віддаленням прогнозного значення Розрахуємо спочатку дисперсію прогнозу. У матричному вигляді дисперсія похибки прогнозу подається так: Середньоквадратична похибка прогнозу Довірчий інтервал для прогнозних значень де ta — критичне значення t-критерію при n – m ступенях свободи і рівні значущості a. Зауважимо, що Для визначення інтервального прогнозу індивідуального значення
Отже, інтервальний прогноз індивідуального значення визначається як
або üПриклад 4.4. Необхідно розрахувати для економетричної моделі (приклад 4.1) точковий та інтервальний прогнози математичого сподівання та індивідуального значення залежної змінної, коли для прогнозного періоду заданий вектор
Розв’язання. 1. Визначимо точкові прогнозні значення залежної змінної, коли
Отже, y0 можна інтерпретувати як точкову оцінку прогнозного значення математичного сподівання та індивідуального значення витрат на харчування, коли відомі загальні витрати x1 = 500 і розмір сім’ї становить x2 = 6. 2. Визначаємо прогнозний інтервал математичного сподівання
Стандартна похибка прогнозу математичного сподівання
3. Знайдемо інтервальний прогноз для Отже,
і 150,62 – 2,160 × 21,95 150,62 – 47,412 103,208 4. Обчислимо дисперсію і стандартну похибку прогнозу індивідуального значення
Стандартна похибка прогнозу індивідуального значення y0 така:
5. Визначимо інтервальний прогноз індивідуального значення y0:
150,62 – 2,160 × 23,467 150,62 – 50,689 99,931 Значення ta знаходимо в таблиці при a = 0,05 і ступені свободи g = 13. У такому разі t0,05 = 2,160. Отже, з імовірністю р = 0,95 (a = 0,05) прогноз математичного сподівання М(y0) потрапляє в інтервал [103,208; 198,032], а прогноз індивідуального значення — в інтервал [99,931; 201,309]. Можна також сказати, що з імовірністю р = 0,95 знайдені прогнози покривають М(y0) і y0, коли взяти досить велику кількість вибірок і для кожної з них обчислити інтервальні прогнози. Економічна інтерпретація: якщо у прогнозному періоді загальні витрати мають рівень 500 одиниць, а сім’я складається з шести осіб, то середні витрати на харчування потрапляють в інтервал 103,208 Водночас окреме (індивідуальне) значення цих витрат міститиметься в ширшому інтервалі: 99,931
4.8. Оцінювання прогнозних можливостей моделі Прогнозування залежної змінної на основі економетричної моделі потребує оцінювання прогнозних можливостей моделі. Для такого оцінювання застосовують систему характеристик, які можна поділити на три групи: · абсолютні; · порівняльні; · якісні. Усі три групи характеристик належать до так званих похибок прогнозу залежної змінної. Абсолютні похибки прогнозу 1. М.Е. — абсолютний показник зміщення прогнозу:
де 2. М.А.Е. — середня абсолютна похибка прогнозу:
3. М.S.E. — середньоквадратична похибка прогнозу:
M.E., M.A.E., M.S.E. — перші літери відповідних англійських назв показників, що використовуються у світовій економетричній літературі. Наведені щойно абсолютні показники якості прогнозу залежать від кількісного рівня залежної змінної, а тому не можуть бути вичерпними характеристиками якості прогнозу. При цьому показник зміщення прогнозу істотно залежить від розміру сукупності спостережень, для якої перевіряються прогнозні можливості побудованої економетричної моделі. Чим більша сукупність спостережень, тим більше впевненості щодо наближення М.Е. до нуля, а отже, щодо відсутності зміщення прогнозу. Розглянемо порівняльні показники оцінювання якості прогнозу. 1. М.Р.Е. — відносний показник зміщення прогнозу:
2. М.А.Р.Е. — середня відносна похибка прогнозу:
КТ — коефіцієнт невідповідності Тейла:
Чим ближчі М.Р.Е. та коефіцієнт невідповідності Тейла до нуля, тим кращі прогнозні якості моделі. Рівень відносного показника М.А.Р.Е. та його тлумачення подано в табл. 4.3. Таблиця 4.3
До якісних оцінок точності прогнозу можна віднести такі показники, що дають можливість провести певний аналіз похибок прогнозу, які трапилися раніше, розкласти їх на окремі складові. Такий аналіз особливо важливий для тих змінних, які можуть циклічно змінюватися, коли необхідно прогнозувати не лише загальний напрям розвитку, а й поворотні точки циклу. У цьому разі середньоквадратична похибка прогнозу дає змогу дослідити: · частку зміщеності (В.Р.); · частку дисперсії (V.P.); · частку коваріації (С.Р.). Очевидно, що в сумі ці частки мають дорівнювати одиниці. Подамо формули розрахунку кожної складової похибки прогнозу.
У цих співвідношеннях Частка зміщеності показує наявність похибки в оцінці основної тенденції, тобто В.Р. > 0 лише тоді, коли середнє арифметичне значення прогнозів відрізняється від середнього арифметичного фактичних даних. Частка дисперсії характеризує ступінь збігу стандартних відхилень прогнозу і фактичних значень, а отже, V.P. = 0 в тому разі, коли дисперсії однакові. Звідси доходимо висновку, що цей показник відбиває відповідність ступеня нестійкості прогнозних значень фактичним даним. Частка коваріації свідчить про ступінь взаємозв’язку між прогнозними і фактичними значеннями. Аналізуючи цей показник можна виокремити ті випадки, коли прогноз задовільний за першими двома показниками (В.Р. і В.Р.), але за наявності коваріації характеризується взаємною компенсацію похибок для різних спостережень. üПриклад 4.5. Оцінити прогнозні якості економетричної моделі, побудованої у прикладі 4.2. Розв’язання.1. Побудуємо економетричну модель на основі 16 спостережень, скориставшись даними табл. 4.2.
Зауважимо, що ця модель істотно відрізняється від моделі, побудованої на основі 20 спостережень (див. приклад 4.2), а також оцінки її параметрів відрізняються від оцінок розглянутої раніше моделі. Коли сукупність спостережень, як у даному разі, невелика, то зміна її завжди буде досить істотно впливати на зміну рівня оцінок параметрів моделі. 2. Підставивши в дану модель значення пояснювальних змінних за останні чотири місяці, дістанемо прогнозовані значення прибутку на ці місяці і запишемо фактичні:
3. Знайдемо відхилення цих розрахункових значень прибутку від фактичних:
Як бачимо, усі значення відхилень (залишків) додатні. Звідси їх модулі та абсолютні значення однакові, а це означає, що збігатимуться М.Е. і М.А.Е., а також М.Р.Е. і М.А.Р.Е. 4. Обчислимо абсолютні та порівняльні характеристики оцінки прогнозних якостей економетричної моделі. 4.1. 4.2. 4.3. 4.4. 4.5. 4.6. Аналізуючи здобуті характеристики, доходимо висновку, що побудована економетрична модель буде давати зміщений прогноз, а це означає, що залишки не є випадковими і ними не можна нехтувати, прогнозуючи прибуток за розглянутою моделлю. Зміщеність прогнозу характеризується порівняно великими значеннями похибок М.Е. та М.Р.Е. Наголосимо, що абсолютне зміщення М.Е. збігається з абсолютною похибкою прогнозу, а це означає, що точковий прогноз може бути зміщеним в бік збільшення. Оскільки відносна похибка прогнозу М.А.Р.Е. = 7,39 % (що менше за 10 %) і коефіцієнт Тейла наближається до нуля, економетричну модель можна використовувати для прогнозування, враховуючи зміщення прогнозу. 4.9. Побудова економетричної моделі |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 322. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 ;
;

 — незалежні, або пояснювальні, змінні;
— незалежні, або пояснювальні, змінні; — параметри функцій.
— параметри функцій. (4.1)
(4.1) (n — кількість спостережень, m — кількість змінних); A — вектор параметрів моделі; u — вектор залишків.
(n — кількість спостережень, m — кількість змінних); A — вектор параметрів моделі; u — вектор залишків. (4.2)
(4.2) (4.3)
(4.3) (4.4)
(4.4) . Тоді суму квадратів залишків u можна записати так:
. Тоді суму квадратів залишків u можна записати так: (4.5)
(4.5) і прирівняємо похідні до нуля:
і прирівняємо похідні до нуля:
 (4.6)
(4.6) (4.7)
(4.7) а потім на матрицю
а потім на матрицю  дістанемо:
дістанемо:
 то справджується рівність
то справджується рівність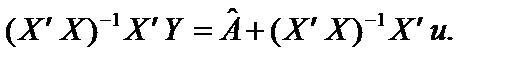
 ,
,  отже,
отже, 

 називають матрицею моментів.
називають матрицею моментів. до нуля і тим гірші оцінки параметрів
до нуля і тим гірші оцінки параметрів  .
.
 ,
, — відповідно фактичні та розрахункові значення за моделлю тижневих витрат на харчування;
— відповідно фактичні та розрахункові значення за моделлю тижневих витрат на харчування; ,
,  ,
,  — оцінки параметрів моделі.
— оцінки параметрів моделі.
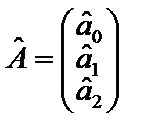 ;
; 
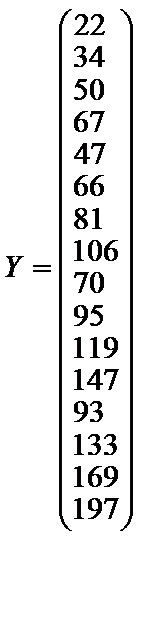
 — матриця, транспонована до матриці X.
— матриця, транспонована до матриці X.
 — середнє значення залежної змінної;
— середнє значення залежної змінної;  ,
,  — середні значення незалежних змінних
— середні значення незалежних змінних  і
і  .
. ;
; ;
;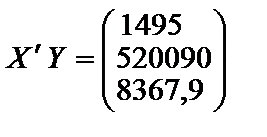 ; 4)
; 4)  .
. .
.

 звідки
звідки .
.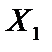 (загальні витрати) збільшується (зменшується) на одиницю, то залежна змінна
(загальні витрати) збільшується (зменшується) на одиницю, то залежна змінна  (оцінка витрат на харчування) збільшується (зменшується) на 0,2 одиниці. Якщо за інших незмінних умов незалежна змінна
(оцінка витрат на харчування) збільшується (зменшується) на 0,2 одиниці. Якщо за інших незмінних умов незалежна змінна  (розмір сім’ї) збільшується (зменшується) на одиницю, то залежна змінна
(розмір сім’ї) збільшується (зменшується) на одиницю, то залежна змінна 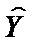 (оцінка витрат на харчування) збільшується (зменшується) на 6,97 одиниці.
(оцінка витрат на харчування) збільшується (зменшується) на 6,97 одиниці.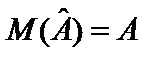 . (4.8)
. (4.8)
 , то
, то  . Отже, оцінка параметрів 1МНК є незміщеною.
. Отже, оцінка параметрів 1МНК є незміщеною. (4.9)
(4.9) і є випадковою величиною, а зміщення — величина стала.
і є випадковою величиною, а зміщення — величина стала. справджується співвідношення
справджується співвідношення (4.10)
(4.10)

 — дисперсія оцінок
— дисперсія оцінок  — дисперсія оцінок
— дисперсія оцінок  , визначених іншими методами.
, визначених іншими методами. — параметр розподілу випадкової величини Â, яка є мірою розсіювання її значень навколо математичного сподівання.
— параметр розподілу випадкової величини Â, яка є мірою розсіювання її значень навколо математичного сподівання. .
. — параметри економетричної моделі;
— параметри економетричної моделі; ,
, .
. ,
,  — оцінки параметрів моделі за сукупністю спостережень.
— оцінки параметрів моделі за сукупністю спостережень.

 .
.
 дістанемо:
дістанемо: .
.
 .
. .
. .
. .
. 0,044037;
0,044037; 1,099585;
1,099585;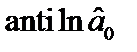 1,045.
1,045.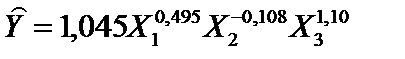 .
. характеризують граничний приріст прибутку залежно від граничного приросту кожного ресурсу на одиницю (коли решта — сталі) і в тих одиницях, в яких вони подаються у вихідній інформації.
характеризують граничний приріст прибутку залежно від граничного приросту кожного ресурсу на одиницю (коли решта — сталі) і в тих одиницях, в яких вони подаються у вихідній інформації. характеризують кількісний зв’язок між прибутком та відповідно кожним ресурсом у відносному (відсотковому) виразі — еластичність. Тому їх потрібно тлумачити так: якщо інвестиції зростуть на 1 %, а основні виробничі фонди і фонд робочого часу не зміняться, то прибуток зросте на 0,495 %
характеризують кількісний зв’язок між прибутком та відповідно кожним ресурсом у відносному (відсотковому) виразі — еластичність. Тому їх потрібно тлумачити так: якщо інвестиції зростуть на 1 %, а основні виробничі фонди і фонд робочого часу не зміняться, то прибуток зросте на 0,495 %  ; якщо основні виробничі фонди зростуть на 1 %, а решта ресурсів буде сталою, то прибуток зменшиться на 0,108 %
; якщо основні виробничі фонди зростуть на 1 %, а решта ресурсів буде сталою, то прибуток зменшиться на 0,108 %  ; і, нарешті, якщо фонд робочого часу зросте на 1 %, і решта ресурсів буде сталою, то прибуток зросте на 1,1 %
; і, нарешті, якщо фонд робочого часу зросте на 1 %, і решта ресурсів буде сталою, то прибуток зросте на 1,1 %  .
. навколо відповідних істинних значень параметрів, що аналізуються, а також характеристики взаємозв’язків отриманих оцінок.
навколо відповідних істинних значень параметрів, що аналізуються, а також характеристики взаємозв’язків отриманих оцінок. і залежний від нього вектор
і залежний від нього вектор  є випадковими змінними. До оператора оцінювання
є випадковими змінними. До оператора оцінювання  входить вектор
входить вектор  , а отже, оператор
, а отже, оператор  і коваріація
і коваріація  (j ¹ k). Істинні (справжні) значення цих параметрів класичної економетричної моделі утворюють дисперсійно-коваріаційну матрицю
(j ¹ k). Істинні (справжні) значення цих параметрів класичної економетричної моделі утворюють дисперсійно-коваріаційну матрицю . (4.12)
. (4.12) використовуються для знаходження стандартних похибок та обчислення довірчих інтервалів оцінок параметрів
використовуються для знаходження стандартних похибок та обчислення довірчих інтервалів оцінок параметрів  містяться оцінки дисперсій
містяться оцінки дисперсій  j-ї оцінки параметрів, що ж до елементів
j-ї оцінки параметрів, що ж до елементів  (j ¹ k), які розміщені поза головною діагоналлю, то вони є оцінками коваріації між
(j ¹ k), які розміщені поза головною діагоналлю, то вони є оцінками коваріації між 
 , (4.13)
, (4.13) — незміщена оцінка дисперсії залишків;
— незміщена оцінка дисперсії залишків;  .
. є так званою узагальненою дисперсією, яка кількісно характеризує ступінь випадкового розсіювання значень векторної випадкової величини навколо свого середнього у відповідному багатовимірному просторі:
є так званою узагальненою дисперсією, яка кількісно характеризує ступінь випадкового розсіювання значень векторної випадкової величини навколо свого середнього у відповідному багатовимірному просторі: . (4.14)
. (4.14)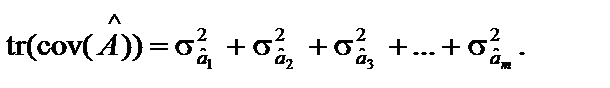 (4.15)
(4.15) , можна стверджувати, що величини, які визначені співвідношеннями (4.14) і (4.15), завжди додатні. Чим більше значення знайдених характеристик (детермінанта, сліду дисперсійно-кореляційної матриці), тим більша загальна варіація оцінок параметрів моделі).
, можна стверджувати, що величини, які визначені співвідношеннями (4.14) і (4.15), завжди додатні. Чим більше значення знайдених характеристик (детермінанта, сліду дисперсійно-кореляційної матриці), тим більша загальна варіація оцінок параметрів моделі). і
і  . (4.16)
. (4.16) , (4.17)
, (4.17) , то добуток векторів
, то добуток векторів  можна записати так:
можна записати так:
 .
. символом
символом  , тоді j-й елемент по головній діагоналі матриці
, тоді j-й елемент по головній діагоналі матриці 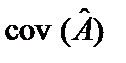 обчислюється за формулою:
обчислюється за формулою: . (4.18)
. (4.18) що містяться за межами головної діагоналі, відповідно такі:
що містяться за межами головної діагоналі, відповідно такі: . (4.19)
. (4.19) .
. ;
;  ;
; ;
; , скориставшись співвідношенням:
, скориставшись співвідношенням: ;
; ;
;
 .
. :
: = 68,92 × 0,314 = 21,64;
= 68,92 × 0,314 = 21,64; = 68,92 × 0,00003 = 0,00207;
= 68,92 × 0,00003 = 0,00207; = 68,92 × 0,0165 = 1,137.
= 68,92 × 0,0165 = 1,137. = 68,92 × (–0,00017) = –0,0118;
= 68,92 × (–0,00017) = –0,0118; = 68,92 × (–0,0446) = –3,0738;
= 68,92 × (–0,0446) = –3,0738;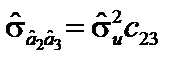 = 68,92 × (–0,00012) = –0,00827.
= 68,92 × (–0,00012) = –0,00827. указує на те, що зі збільшенням однієї оцінки параметрів інша зменшується в середньому і навпаки.
указує на те, що зі збільшенням однієї оцінки параметрів інша зменшується в середньому і навпаки. .
. ;
; ;
; ;
; .
. з відповідним числовим значенням оцінки параметра, тобто знайдемо відношення
з відповідним числовим значенням оцінки параметра, тобто знайдемо відношення  :
: ;
; ;
; .
. (4.20)
(4.20) );
);  — вагові коефіцієнти значень
— вагові коефіцієнти значень  (їх потрібно вибрати так, щоб значення
(їх потрібно вибрати так, щоб значення  було найкращим лінійним незміщеним прогнозом).
було найкращим лінійним незміщеним прогнозом). то незміщена точкова оцінка прогнозу
то незміщена точкова оцінка прогнозу (4.21)
(4.21)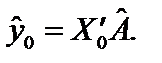 (4.22)
(4.22) від відповідного середнього значення вибірки.
від відповідного середнього значення вибірки. . (4.23)
. (4.23)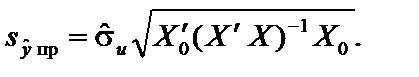 (4.24)
(4.24) (4.25)
(4.25) є точковою оцінкою як математичного сподівання прогнозного значення
є точковою оцінкою як математичного сподівання прогнозного значення  , так і його індивідуального значення
, так і його індивідуального значення  , що лежить за межами базового періоду.
, що лежить за межами базового періоду. необхідно знайти відповідну стандартну похибку:
необхідно знайти відповідну стандартну похибку:


 .
.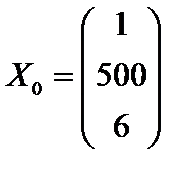 : то
: то  .
. :
:


 .
. . При цьому нехай a = 0,05 і n – m = 13; тоді t0,05 = 2,160.
. При цьому нехай a = 0,05 і n – m = 13; тоді t0,05 = 2,160.
 150,62 + 2,160 × 21,95;
150,62 + 2,160 × 21,95; 150,62 + 47,412;
150,62 + 47,412; 198,032.
198,032. .
. .
. ;
; 150,62 + 2,160 × 23,467;
150,62 + 2,160 × 23,467; 150,62 + 50,689;
150,62 + 50,689; 201,309.
201,309. 198,032.
198,032. 201,309.
201,309. ,
, — кількість спостережень
— кількість спостережень  ;
;  — відповідно фактичні та розрахункові значення залежної змінної.
— відповідно фактичні та розрахункові значення залежної змінної.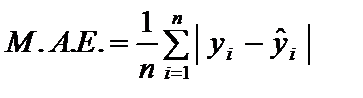 .
.
 .
. .
.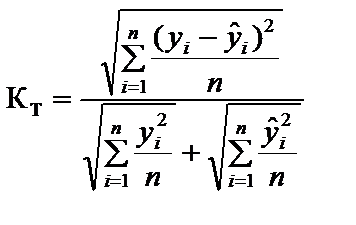 .
. ;
;  ;
; .
. — стандартна похибка прогнозу; Sy — стандартна похибка фактичних значень залежної змінної; R — коефіцієнт кореляції; yпр — прогнозне значення залежної змінної.
— стандартна похибка прогнозу; Sy — стандартна похибка фактичних значень залежної змінної; R — коефіцієнт кореляції; yпр — прогнозне значення залежної змінної.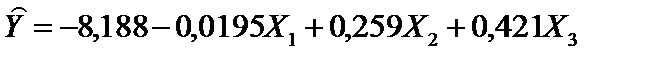 .
.