
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ТЕПЛОВОЙ ПОТОК. ВЕКТОРНАЯ И СКАЛЯРНАЯ ФОРМЫ ЗАКОНА ФУРЬЕСтр 1 из 8Следующая ⇒ ТЕМПЕРАТУРНЫЙ ГРАДИЕНТ Рассмотрим две бесконечно близкие изотермические поверхности с температурами
Производная функции
Рис. 1.4 Схема к определению теплового потока
Наибольшая разность температур на единицу длины вектора перемещения
Таким образом, в любой точке  в декартовых координатах
в цилиндрических координатах
в сферических координатах
Для обозначения вектора (1.5) в теории поля иногда применяют символ Согласно сказанному выше, можно записать:
т. е. длина вектора Производная от функции
Вектор нормали
ТЕПЛОВОЙ ПОТОК. ВЕКТОРНАЯ И СКАЛЯРНАЯ ФОРМЫ ЗАКОНА ФУРЬЕ В теле, не находящемся в полном тепловом равновесии (т. е. обладающим неравномерным распределением температуры), всегда происходит перенос теплоты. Отсюда следует, что для передачи теплоты теплопроводностью необходимо неравенство нулю температурного градиента. В этом смысле температурный градиент является основным физическим параметром, определяющим условие возникновения теплового процесса. Следовательно, соотношение
Формула (1.10) характеризует плотность теплового потока единичного элемента изотермической поверхности. Понятие плотности теплового потока, как будет показано ниже, применимо к любой, а не только к изотермической, поверхности. Опыт показывает, что передача теплоты теплопроводностью происходит по нормали к изотермической поверхности от участков тела с большей к участкам с меньшей температурой. Следовательно, вектор плотности теплового потока направлен по нормали к изотермической поверхности в направлении уменьшения температуры. Можно говорить о плотности теплового потока и вдоль любого другого направления Идея о существовании органической связи между вектором плотности теплового потока и температурным градиентом легла в основу учения, созданного Фурье. Сущность гипотезы Фурье состоит в том, что тепловой поток через элемент изотермической поверхности вполне определяется значением температурного градиента в рассматриваемой точке ры плотности теплового потока С увеличением перепада температур, т. е. с возрастанием температурного градиента, увеличивается и плотность теплового потока. Опыты показали, что плотность теплового потока можно считать пропорциональной первой степени удельного перепада температуры. Это и явилось основой гипотезы Фурье о наличии простейшей количественной зависимости между абсолютными значениями векторов плотности теплового потока и температурного градиента. На основе этих данных, а также соображений о противоположном направлении этих векторов, закон Фурье в векторном виде записывается следующим образом:
Этот закон, сформулированный в виде гипотезы, был подтвержден многочисленными опытами. Выражение (1.11) используется при выводе уравнений, описывающих механизм процесса теплопроводности. Наглядное представление о мгновенном распределении потоков теплоты могут дать линии, касательные к которым в каждой точке температурного поля совпадают с соответствующими нормалями к изотермическим поверхностям. Такие линии называются линиями теплового потока (рис. 1.5).
Рис. 1.5 Направление векторов плотности теплового потока и градиента температуры
Коэффициент пропорциональности Числовое значение теплопроводности определяет количество теплоты, проходящее через единицу площади изотермической поверхности в единицу времени при градиенте температуры, равном единице. Подобно другим величинам этого ряда (удельная теплоемкость, электрическое сопротивление, модуль упругости и т. п.) значение теплопроводности в общем случае зависит от природы вещества, его структуры, влажности, давления, температуры и других факторов. В большинстве случаев теплопроводность Зависимость теплопроводности от температуры в общем случае довольно сложная, однако для большинства твердых тел, жидкостей и газов при умеренных температурах она оказывается почти линейной, т. е. Соотношение (1.10) запишем в виде:
Как отмечалось выше, нормаль
Действительно, для нормали, совпадающей с направлением градиента, имеем
Выражение (1.14) определяет количество теплоты, проходящее через элементарный участок
Тепловой поток может быть определен вдоль любого направления через площадь, перпендикулярную этому направлению. Однако на практике часто встречаются случаи, когда площадка ориентирована в поле произвольным образом. Покажем, что равенство (1.14) справедливо для любых поверхностей, а не только для изотермических.
Рис. 1.6 Изотермическая поверхность
Выберем произвольную элементарную площадку
так как Отсюда находим, что
Общее количество теплоты, протекающее за время
В частном случае, когда тепловой режим стационарный и температурный градиент одинаков по всей площади поверхности
Рис. 1.7 Схема к определению теплового потока
Таким образом, для определения количества теплоты, проходящей через какую-либо площадь поверхности твердого тела, нужно знать температурное поле внутри данного тела, что составляет главную задачу аналитической теории теплопроводности. Так как В этом параграфе не рассматриваются усложненные анизотропией случаи теплопроводности. Для таких веществ как древесина, слюда и т. п., теплопроводность Если спроектировать вектор плотности теплового потока на координатные оси, то в соответствии с его определением (1.11) можно записать:
Тепловые потоки, выраженные соотношениями (1.18), являются составляющими вектора плотности теплового потока. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 223. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  и какую-либо точку
и какую-либо точку  , лежащую на одной из них (рис. 1.4). Перемещаясь из точки
, лежащую на одной из них (рис. 1.4). Перемещаясь из точки  , пересекающего изотермические поверхности, то наблюдается изменение температуры. Используя понятие производной скалярного поля по заданному направлению, можно описать его локальные свойства, т. е. изменение температуры
, пересекающего изотермические поверхности, то наблюдается изменение температуры. Используя понятие производной скалярного поля по заданному направлению, можно описать его локальные свойства, т. е. изменение температуры  по направлению
по направлению  . (1.3)
. (1.3) по направлению
по направлению  вычисляется по формуле:
вычисляется по формуле: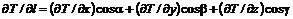 .
.
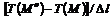 наблюдается в направлении нормали
наблюдается в направлении нормали  к изотермической поверхности (рис. 1.4). В соответствии с (1.3) максимальная скорость изменения температуры при этом равна пределу отношения изменения температуры
к изотермической поверхности (рис. 1.4). В соответствии с (1.3) максимальная скорость изменения температуры при этом равна пределу отношения изменения температуры  к расстоянию между изотермическими поверхностями по нормали
к расстоянию между изотермическими поверхностями по нормали  , когда
, когда  . (1.4)
. (1.4) :
: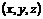
 ; (1.5)
; (1.5)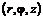
 ; (1.6)
; (1.6)
 . (1.7)
. (1.7) .
. , (1.8)
, (1.8) . (1.9)
. (1.9) в точке
в точке  является необходимым условием возникновения внутри тела теплового потока. Тепловой поток в отличие от температуры (величины скалярной) имеет вполне определенное направление, а именно: от точек тела с более высокой к точкам с более низкой температурой. Таким образом, тепловой поток можно рассматривать как вектор, направленный в сторону уменьшения температуры, а поле тепловых потоков – векторным. Для математического описания поля тепловых потоков вводится вектор
является необходимым условием возникновения внутри тела теплового потока. Тепловой поток в отличие от температуры (величины скалярной) имеет вполне определенное направление, а именно: от точек тела с более высокой к точкам с более низкой температурой. Таким образом, тепловой поток можно рассматривать как вектор, направленный в сторону уменьшения температуры, а поле тепловых потоков – векторным. Для математического описания поля тепловых потоков вводится вектор  , называемый вектором плотности теплового потока. Под вектором плотности теплового потока в точке
, называемый вектором плотности теплового потока. Под вектором плотности теплового потока в точке 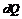 количество теплоты, проходящее через изотермическую поверхность площади
количество теплоты, проходящее через изотермическую поверхность площади  за время
за время  . Тогда абсолютное значение вектора плотности теплового потока можно записать в виде:
. Тогда абсолютное значение вектора плотности теплового потока можно записать в виде: . (1.10)
. (1.10) .
. . (1.11)
. (1.11)
 называется теплопроводностью и является физической константой, характеризующей теплопроводящие свойства материала данного тела. Подставляя в уравнение (1.11) единицы
называется теплопроводностью и является физической константой, характеризующей теплопроводящие свойства материала данного тела. Подставляя в уравнение (1.11) единицы  , где
, где  – теплопроводность при температуре
– теплопроводность при температуре  ; b – постоянная, определяемая опытным путем. В классической аналитической теории теплопроводности величина
; b – постоянная, определяемая опытным путем. В классической аналитической теории теплопроводности величина  ).
). . (1.12)
. (1.12) . Теперь в равенстве (1.8) необходимо поставить знак минус, т. е.
. Теперь в равенстве (1.8) необходимо поставить знак минус, т. е.  и
и . (1.13)
. (1.13) ; перенос же теплоты происходит всегда в направлении уменьшения температуры, т. е. в противоположную сторону и, следовательно, должно быть
; перенос же теплоты происходит всегда в направлении уменьшения температуры, т. е. в противоположную сторону и, следовательно, должно быть  , или, что то же самое,
, или, что то же самое,  , что и объясняет знак минус в формуле (1.13). Изменив направление нормали на противоположное, имеем
, что и объясняет знак минус в формуле (1.13). Изменив направление нормали на противоположное, имеем  , но тогда
, но тогда 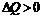 и, следовательно, знак минус сохраняется. Подставляя теперь в (1.12) вместо
и, следовательно, знак минус сохраняется. Подставляя теперь в (1.12) вместо  правую часть равенства (1.13), можно записать закон Фурье в скалярной форме:
правую часть равенства (1.13), можно записать закон Фурье в скалярной форме: . (1.14)
. (1.14)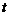 через изотермическую поверхность конечных размеров площадью
через изотермическую поверхность конечных размеров площадью  будет определяться по соотношению:
будет определяться по соотношению: .
.
 так, чтобы угол между нормалью
так, чтобы угол между нормалью  к ней и вектором плотности теплового потока
к ней и вектором плотности теплового потока  в рассматриваемой точке был равен
в рассматриваемой точке был равен  (рис. 1.7). Поток теплоты по нормали
(рис. 1.7). Поток теплоты по нормали 
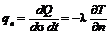 ;
; ,
, .
. . (1.16)
. (1.16) :
: . (1.17)
. (1.17)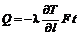 .
.
 является составляющей вектора плотности теплового потока
является составляющей вектора плотности теплового потока  , то из этого уравнения следует, что самым большим тепловым потоком, отнесенным к единице площади поверхности, будет тот, который рассчитан вдоль нормали
, то из этого уравнения следует, что самым большим тепловым потоком, отнесенным к единице площади поверхности, будет тот, который рассчитан вдоль нормали  .
. (1.18)
(1.18)