
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вопрос №35. «Односторонняя» модель Эрроу-Гурвица.Здесь будет рассмотрена модель, в которой в виде участвующих субъектов участвуют: 1. Два предприятия, использующие один и тот же ресурс (труд L) и производящие один и тот же вид продукции Y. Производственная функция здесь имеет вид:
2. Функция полезности с точки зрения потребителей имеет вид:
Потребители стремятся максимизировать функцию полезности, производители - функцию прибыли, выражаемую следующей формулой: где
В модели рассматривается рынок совершенной (абсолютной) конкуренции. Исходные данные модели Эрроу-Гурвица 1. 2. 3. 4. 5. 6. Реакция предприятия на цены А. Б.
Реакция потребителей на цены Потребитель определяет объем спроса пропорционально разнице между предельной полезностью и предельными затратами:
Корректировка цен:
Если если если Практический пример Исходные данные модели Эрроу-Гурвица
Необходимо определить состояние равновесия с точностью 1,5  Реакция предприятия на цены
Реакция потребителя на цены
Равновесие не достигнуто, так как избыточный спрос превышает требуемую величину в 1,5. Цена возрастает. Проведем интерацию №1.
Равновесие не достигнуто Проведем интерацию №2.
Вывод: равновесие было достигнуто после проведения второй интерации. Вопрос №36. Модель Солоу. Модель названа в честь экономиста Роберта Солоу и была разработана в 1950-1969 гг. В 1987 г. Модель Солоу позволяет оценивать разные варианты экономической политики государства, ее влияние на уровень жизни, прогнозировать, какая часть произведенного продукта должна потребляться сегодня, а какая его часть должна сберегаться для увеличения потребления в будущем. Поскольку сбережения равны инвестициям, то именно они определяют объём капитала, которым экономика будет располагать в будущем. В модели показаны, как рост запасов капитала, рабочей силы и улучшение технологии воздействуют на объём производства, а, следовательно, на темпы экономического роста национального дохода во времени. Накопление капитала. В своей модели Р. Солоу исходит из классической предпосылки теории рыночного равновесия, что спрос на товары предъявляется со стороны: потребителей; инвесторов. Другими словами, продукция, произведенная каждым рабочим, делится между потреблением, приходящимся на одного рабочего, и инвестициями в расчете на одного рабочего: y = c + i. Это уравнение сходно с тождеством национальных счетов. Модель Солоу предполагает, что функция потребления принимает простую форму: С = (1 – S) Y, где s(норма сбережений) принимает значения от 0 до 1. Эта функция означает, что потребление пропорционально доходу. Каждый год часть дохода Y потребляется (1 – s) и часть сберегается (s). Роль такой трактовки потребления выяснится, если мы заменим в тождестве национальных счетов величинуc (потребление) на (1 – s) y, тогда оно будет иметь следующий вид: Y = (1-S) Y + I. После преобразования получим: i = sy. Это уравнение показывает, что I (инвестиции), как и потребление, пропорциональны доходу. Если инвестиции равны сбережениям, то норма сбережений (s)показывает, какая часть произведенной продукции направляется на капитальные вложения. Представив модель Солоу как функцию производства и как функцию потребления, можно проанализировать, как накопление капитала обеспечивает экономический рост страны. Общая величина капитала в национальной экономике может изменяться по двум причинам: 1) инвестиции приводят к росту объемов капитала; 2) часть капитала изнашивается, то есть амортизируется, что приводит к его уменьшению. Для того, чтобы понять, как изменяется объем капитала, необходимо выявить факторы, определяющие величину инвестиций и амортизации. Инвестиции(i) в расчете на одного работника, занятого в отраслях национальной экономики, являются частью валового внутреннего продукта, приходящегося на одного работника (sу). Заменив (y) выражением производственной функции y = f(k), представим инвестиции на одного работника как функцию от капиталовооруженности национальной экономики: i = sf (k). Из данного уравнения следует, что чем выше уровень капиталовооруженности k, тем выше объём производства f(k) и больше инвестиций i. |
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 498. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 где
где 
 - спрос на труд со стороны предприятия i
- спрос на труд со стороны предприятия i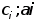 - параметры производственной функции.
- параметры производственной функции.
 - цена производимого продукта
- цена производимого продукта - объем выпуска фирмы i
- объем выпуска фирмы i - цена ресурса (труда)
- цена ресурса (труда) - цена на продукцию в предшествующем периоде,
- цена на продукцию в предшествующем периоде,  - цена на ресурс в предшествующем периоде,
- цена на ресурс в предшествующем периоде,  - предложение труда
- предложение труда - спрос предшествующего периода на продукцию фирмы i,
- спрос предшествующего периода на продукцию фирмы i,  - параметры функции полезности и производственной функции
- параметры функции полезности и производственной функции - коэффициент корректировки цен.
- коэффициент корректировки цен. - размер спроса на ресурсы
- размер спроса на ресурсы - размер предложения продукта
- размер предложения продукта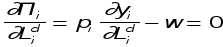





 ;
; 

 - коэффициент пропорциональности, ускоряющий процесс сходимости итераций.
- коэффициент пропорциональности, ускоряющий процесс сходимости итераций. - избыточный спрос на продукт
- избыточный спрос на продукт - избыточный спрос на ресурс
- избыточный спрос на ресурс
 , то цены увеличиваются,
, то цены увеличиваются, , то цены падают,
, то цены падают, , то цены не меняются - система в состоянии равновесия
, то цены не меняются - система в состоянии равновесия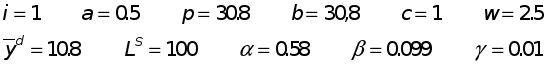


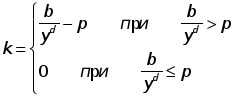


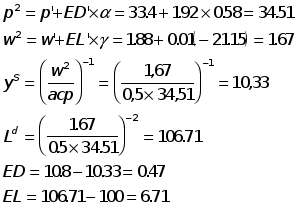
 - равновесие достигнуто с заданной точностью. Результат:
- равновесие достигнуто с заданной точностью. Результат: