
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Что такое передаточное отношение (число) механической передачи и как распределить его по ступеням привода?
1. Определить частоту вращения приводного вала рабочей машины nр.м, об/мин: а) для ленточных конвейеров, грузоподъемных и прочих машин:
отсюда
где v — скорость тягового органа, м/с; D – диаметр барабана, мм; б) для цепных конвейеров:
отсюда
где v – скорость конвейера, м/с; z – число зубьев ведущей звездочки тягового органа; р – шаг тяговой цепи, мм. 2. Определить передаточное число привода для всех приемлемых вариантов типа двигателя при заданной номинальной мощности Рном :
3.Определить передаточные числа ступеней привода. Определение и выбор передаточных чисел ступеней произвести разбивкой передаточного числа привода для всех вариантов типа двигателя так, чтобы u1 = uз.п1∙uо.п1; u2 = uз.п2∙uо.п2; u3 = uз.п3∙uо.п3; …, где u, uз.п, uо.п – соответственно передаточные числа привода, редуктора и открытой передачи (см. табл. 19). При этом возможны три способа разбивки передаточного числа и (выбирая способ, учесть стандартность передаточного числа закрытой передачи-редуктора uз.п и нестандартность передаточного числа uо.п – открытой): а) оставить передаточное число редуктора uз.п постоянным, изменяя передаточное число открытой передачи uо.п:
б) оставить передаточное число открытой передачи uо.п постоянным, изменяя передаточные числа редуктора uз.п:
в) наметить конкретные значения передаточных чисел редуктора uз.п и открытой передачи uо.п для первого варианта, а в последующих вариантах получать передаточные числа ступеней умножением предыдущих чисел на соответствующий множитель К:  для 2-го варианта для 3-го варианта Тогда для 2-го варианта uз.п2 = uз.п1K2; uо.п2 = uо.п1K2; для 3-го варианта uз.п3 = uз.п2K3; uо.п3 = uо.п2K3 и т.д. Разбивка передаточного числа привода и должна обеспечить компактность каждой ступени передачи и соразмерность ее элементов.
Для того чтобы габариты передач не были чрезмерно большими, нужно придерживаться некоторых средних значений uз.п и uо.п, по возможности не доводя их до наибольших, допускаемых лишь в отдельных случаях. Определить максимальное допускаемое отклонение частоты вращения приводного вала рабочей машины Δn, об/мин:
где δ, % — допускаемое отклонение скорости приводного вала рабочей машины (см. технические задания). 5. Определить допускаемую частоту вращения приводного вала рабочей машины с учетом отклонения [nр.м], об/мин: [nр.м] = nр.м ± Δnр.м. При этом [nр.м] может существенно повлиять на предварительную разбивку передаточного числа привода u. Поэтому оптимальные передаточные числа uз.п и uо.п можно получить подбором необходимого значения допускаемого отклонения частоты вращения в пределах максимального: от –Δnр.м до + Δnр.м (в том числе Δnр.м = 0).
Что такое коэффициент полезного действия передачи и как он определяется в целом для электромеханического привода? КПД это отношение полезной мощности (на выходе) к затраченной на входе.
где
|
|||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 995. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 ,
, ,
, ,
, ,
,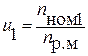 ,
, ,
,
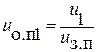 ;
;  ;
;  ;…
;… ;
;  ;
; 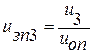 ;…
;…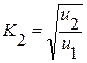 ;
; и т.д.
и т.д.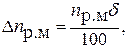
 (4)
(4)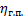 – кпд гибкой передачи,
– кпд гибкой передачи,  – кпд зубчатой передачи,
– кпд зубчатой передачи, – кпд подш-в качения, n – число пар подшипников.
– кпд подш-в качения, n – число пар подшипников.