Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Понятие момента инерции тела. Пример расчета. Теорема Штейнера.Моментом инœерции J материальной точки относительно оси принято называть скалярная физическая величина, равная произведению массы m на квадрат расстояния r до этой оси: J = mr2 (75) Теорема Штейнера. Эта теорема применяется для расчета моментов инерции тел, если ось вращения не проходит через центр инерции тела (его центр масс): момент инерцииIтела относительно произвольной оси равен сумме момента инерции
Основное уравнение динамики вращательного движения твердого тела. Закон сохранения момента импульс. Основное уравнение динамики вращательного движения Чтобы описать вращательное движение, связав причину движения (воздействующую силу) и следствие (приобретение углового ускорения), используют основное уравнение динамики вращательного движения:
Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени
Свободное незатухающие механические колебания. Свободные колебания могут быть незатухающими только при отсутствии силы трения. В противном случае первоначальный запас энергии будет расходоваться на ее преодоление, и размах колебаний будет уменьшаться
Физический и математический маятник. Уравнение колебаний. Математический маятник- материальная точка, подвешенная на невесомой нерастяжимой нити 
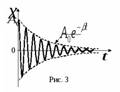
Физический маятник - твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси Уравнение гармонических колебаний: где t-время; x-величина изменяющаяся со временем (координата, заряд, ток, ЭДС и т.п.); A- амплитуда колебаний – максимальное отклонение колеблющейся величины от среднего (нулевого) значения; Дифференциальное уравнение гармонических колебаний Уравнение вида: 9. Свободные затухающие механические колебания. Коэффициент и логарифмический декремент затухания.. Затухающие колебания- это колебания, амплитуда которых убывает со временем. Для пружинного маятника массой m, совершающего малые колебания под действием упругой силы где r- коэффициент сопротивления среды; знак минус означает, что
Логарифмический декремент затухания равен натуральному логарифму отношения амплитуды предыдущего колебания к амплитуде последующего колебания. коэффициент затухания – величина, обратная времени релаксации. А время релаксации – это время, за которое амплитуда уменьшается в e раз. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 558. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 тела относительно оси, проходящей через центр массы С данного тела и параллельной заданной оси, и произведения массы m тела на квадрат расстояния между этими осямиI = IC + md2.
тела относительно оси, проходящей через центр массы С данного тела и параллельной заданной оси, и произведения массы m тела на квадрат расстояния между этими осямиI = IC + md2.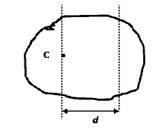
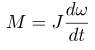 Здесь
Здесь 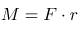 – момент силы, характеризующий, насколько интенсивно сила воздействует на тело.
– момент силы, характеризующий, насколько интенсивно сила воздействует на тело.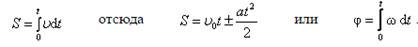
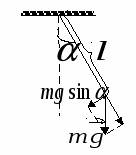
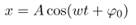
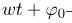 — фаза колебаний;
— фаза колебаний; 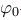 — начальная фаза; w- циклическая частота (изменение фазы в единицу времени). За период фаза меняется на
— начальная фаза; w- циклическая частота (изменение фазы в единицу времени). За период фаза меняется на 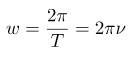
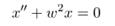
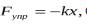 сила трения пропорциональна скорости:
сила трения пропорциональна скорости: 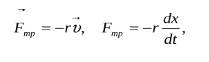
 всегда направлена противоположно скорости.
всегда направлена противоположно скорости.