Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Понятие момента импульса и момента силы относительно точки и неподвижной оси вращения. Уравнение моментов.Стр 1 из 19Следующая ⇒ Вопросы для односеместрового курса Кинематика движения материальной точки. Траектория, радиус-вектор, перемещение, путь, скорость, ускорение. Кинематика движения по окружности. Перемещение – это вектор Δ ,соединяющий начальное и конечное положение точки Скорость (мгновенная скорость) – это векторная величина , равная производной перемещения по времени Ускорение (мгновенное ускорение) – векторная величина , равная производной от скорости по времени
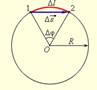
Радиус-вектор точки - это вектор, начало которого совпадает с началом системы координат, а конец - с данной точкой. Траектория - непрерывная линия, вдоль которой движется материальная точка в заданной системе отсчета. Движение тела по окружности является частным случаем криволинейного движения. Наряду с вектором перемещения удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах Длина дуги связана с углом поворота соотношением
При малых углах поворота Δl ≈ Δs. Динамика материальной токи. Законы Ньютона. Импульс. Закон сохранения импульса. Первый закон Ньютона: если на тело (точку) не действуют силы, оно сохраняет состояние покоя или прямолинейного равномерного движения. Импульс материальной точки – это произведение ее массы на скорость Второй закон Ньютона или основное уравнение динамики : скорость изменения импульса материальной точки (тела) равна векторной сумме приложенных сил  В частном случае, если масса тела не изменяется в процессе движения, второй закон Ньютона имеет вид в векторной форме записи Третий закон Ньютона: два тела взаимодействуют с силами, равными по величине и противоположно направленными. Закон сохранения импульса а) Если система замкнута, т. е. внешние силы отсутствуют, или если их сумма равна нулю, то импульс системы сохраняется: Σp = const. б) Если внешние силы перпендикулярны некоторой оси x, то проекция импульса системы на это направление сохраняется: Σpx = const .в) Если время взаимодействия мало (взрыв, удар), а внешняя сила имеет фиксированную величину (например, mg), то вкладом импульса этой силы FΔt в изменение импульса системы можно пренебречь.3. Работа постоянной силы. Потенциальная и кинетическая энергия. Закон сохранения механической энергии. Кинетическая энергия материальной точки массы m (тела, движущегося поступательно) 44 m pmv E 22 22 == . (3.14) Если частица массы m движется под действием k сил , то приращение ее кинетической энергии при перемещении из точки 1 в точку 2 равно алгебраической сумме работ всех сил на этом пути FFFF k ,....,, 321 ∑ ( = =−=Δ k j kkk FAEEE j 1 12 12 ). Потенциальная энергия частицы, находящейся в точке поля с координатами (х,у,z), - это скалярная величина ( ) 000 = ,,,,, zyxzyxUU , равная взятой со знаком минус работе консервативных сил поля по перемещению частицы с уровня принятого за ноль отсчета потенциальной энергии ( ) 0,, zyxU 000 = в данную точку. ( ) −= AzyxUконс ,, . Закон сохранения полной механической энергии constUEE (3.23) = K + = выполняется, если на систему действуют только консервативные силы. В частном случае, если система замкнута, а внутренние силы консервативны, полная механическая энергия сохраняется. Работа постоянной силы FSrFA cosα=Δ=Δ r r . Понятие момента импульса и момента силы относительно точки и неподвижной оси вращения. Уравнение моментов.
Моментом силы относительно точки называется взятое со знаком ( плюс или минус) произведение модуля силы на кратчайшее расстояние от точки до линии действия силы
Основное уравнение динамики вращательного движения в наиболее общем виде выглядит так: Момент импульса Моментом силы относительно неподвижной оси z называется скалярная величина Mz , равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z |
|||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 617. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
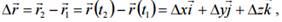
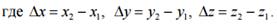
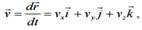 где –VxVyVz проекции вектора скорости на оси координат. Вектор v направлен по касательной к траектории
где –VxVyVz проекции вектора скорости на оси координат. Вектор v направлен по касательной к траектории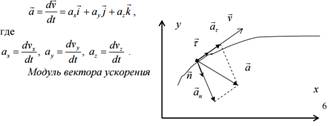
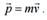
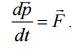
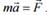 .
.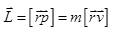
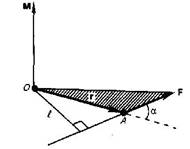
 относительно оси - это проекция на данную ось момента импульса L, определенного относительно некоторой точки О, принадлежащей оси, причем, как оказывается, выбор точки О на оси значения не имеет.
относительно оси - это проекция на данную ось момента импульса L, определенного относительно некоторой точки О, принадлежащей оси, причем, как оказывается, выбор точки О на оси значения не имеет.