
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ОПИСАНИЕ УСТАНОВКИ И МЕТОДА РАСЧЁТА
Прибор (рис. 2) состоит из призмы 1, закреплённой с помощью штифта в стойке 2. Стойка прибора установлена в треноге 3, две ножки которой снабжены винтами 4. Это позволяет установить прибор по имеющемуся на нём уровню 5 так, чтобы опорное ребро призмы приняло горизонтальное положение. К стойке винтами прикреплена планка 6 клиновидной формы с углом при вершине 7о, которая позволяет следить, чтобы размах колебаний физического маятника не превосходил угол 7о.
Рисунок 2 – Установка для изучения законов колебания физического маятника
В формулу (6) входит Момент инерции вводится для тела, участвующего во вращательном движении и характеризует инертные свойства тела. Для материальной точки момент инерции равен Если тело имеет произвольную форму, то чтобы найти момент инерции, поступим следующим образом. Разобьём тело на
При
где
Рисунок 3 – Определение момента инерции для тела с непрерывным распределением массы
Вычисление моментов инерции через интеграл является простой задачей только для тел сравнительно простой формы и относительно осей симметрии, проходящих через центры масс тела. Момент инерции 
Теорема Штейнера: момент инерции
Для примера применим теорему Штейнера для нахождения относительно оси О1О1 для однородного стержня (рис. 4)
Однородный Однородный Однородный Тонкостенный стержень диск (цилиндр) шар цилиндр (обруч)
Рисунок 4 – Применение теоремы Штейнера
Запишем теорему Штейнера:
С учётом вышеизложенного, теорема Штейнера запишется в виде:
Задание: Найдите самостоятельно моменты инерции
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 688. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 - момент инерции маятника относительно оси
- момент инерции маятника относительно оси  .
. , где
, где  - расстояние точки до оси, относительно которой находится момент инерции.
- расстояние точки до оси, относительно которой находится момент инерции. частей, причём
частей, причём  .
. эта сумма в пределе переходит в интеграл:
эта сумма в пределе переходит в интеграл: ,
,  ,
, - плотность вещества,
- плотность вещества,  - элемент объёма.
- элемент объёма.
 некоторых тел, вычисленных относительно оси вращения, проходящей через центр масс
некоторых тел, вычисленных относительно оси вращения, проходящей через центр масс












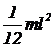
 Если ось, относительно которой считается момент инерции, не проходит через центр тяжести, то момент инерции находится по теореме Штейнера.
Если ось, относительно которой считается момент инерции, не проходит через центр тяжести, то момент инерции находится по теореме Штейнера. относительно произвольной оси равен сумме его момента инерции
относительно произвольной оси равен сумме его момента инерции 

 ,
, - момент инерции однородного стержня относительно оси проходящей через центр тяжести тела;
- момент инерции однородного стержня относительно оси проходящей через центр тяжести тела; - расстояние между осями.
- расстояние между осями. .
. для остальных тел, приведённых на рисунке 4.
для остальных тел, приведённых на рисунке 4.