
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методика нахождения абсолютной погрешности с использованием дифференциала функцииПри работе с величинами, значение которых известно лишь приближенно, часто бывает необходимо определить результирующую погрешность формулы, в которой используются эти величины. Решение этой задачи может быть получено посредством вычисления дифференциала функции, выражающей эту формулу. Рассмотрим методику нахождения абсолютной погрешности с использованием дифференциала функции для вывода приближенных формул. Покажем вывод приближения, на примере функции трёх переменных. Пусть в результате измерений и последующей обработки получены приближённые значения трёх величин с надёжностью P0=0,9:
Пусть далее, имеется функция (формула) включающая эти величины:
Подставляя средние значения величин
Погрешность (отклонение) функции
Правомерность приближения определяется по смыслу - погрешность измеряемой величины много меньше её значения. Таким образом, мы имеем с той же надёжностью:
Обобщение формулы на произвольное количество измеряемых величин очевидно. По мере приобретения навыка вычисления, рекомендуется выводить формулу погрешности в форме ряда Тейлора, с удержанием линейных членов разложения:
Рассмотрим несколько примеров. Пример 1. Момент инерции полого цилиндра, может быть вычислен по формуле:
где m -масса цилиндра, R0 - внутренний радиус, R1 - внешний радиус. Их приближённые значения составляют:
Определить момент инерции цилиндра и его погрешность. Решение. Момент инерции цилиндра очевидно равен: 
Выведем формулу погрешности ΔI, для чего вычислим частные производные:
Запишем формулу погрешности:
Подставляя числовые значения, получим:
Пример 2. Стартовая масса M0 ракеты для достижения скорости V должна составлять:
M - конечная масса ракеты, С - скорость газа в реактивной струе. Значения и допустимые отклонения начальных параметров составляют:
Определить начальную массу ракеты и допустимое отклонение. Решение.Разлагая формулу Циолковского в ряд Тейлора, и оставляя линейные члены разложения, будем иметь:
Вычисляя частные производные, получим расчётную формулу:
Подставляя числовые значения, имеем:
Пример 3.Некоторая величина имеет приближённое значение:
Определить приближённое значение формулы:
Решение. Используя линейные члены разложения ряда Тейлора, имеем:
Для свободного владения методом рекомендуется вывести формулы погрешностей используя произвольные комбинаций элементарных функций. В дальнейшем при проведении лабораторных работ и их анализа, предлагается самостоятельно вычислить абсолютную погрешность, используя дифференциал функции формулы (1) и (2). В качестве примера, в лабораторной работе №1, будет подробно рассмотрено нахождение абсолютной погрешности объёма цилиндра. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 611. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
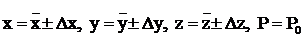 .
. .
.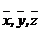 , определим среднее значение функции:
, определим среднее значение функции: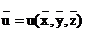 .
.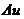 , при отклонении исходных величин,
, при отклонении исходных величин, 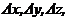 может быть приближённо выражена дифференциалом самой функции, т.е.:
может быть приближённо выражена дифференциалом самой функции, т.е.: (1)
(1)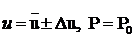 .
.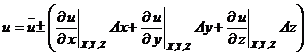 (2).
(2).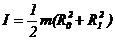 ,
,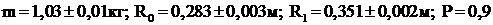 .
.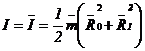 .
.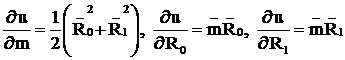 .
.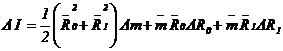 .
.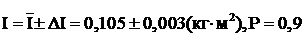 .
.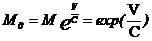 (формула Циолковского).
(формула Циолковского).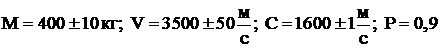 .
.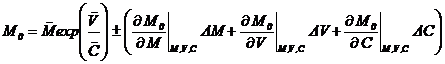 .
.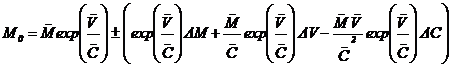 .
.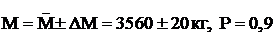 .
.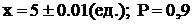 .
.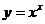 .
.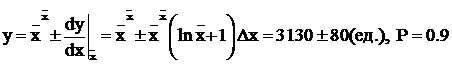 .
.