
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные свойства дисперсии1. Если из каждого значения варианты отнять (прибавить) одно и то же постоянное число А, то средний квадрат отклонений от этого не изменится: 2. Если каждое значение вариант разделить или умножить на одно и то же постоянное число А,то дисперсия уменьшится (увеличится) от этого в А2раз, а стандартное отклонение (среднее квадратическое отклонение) – в А раз: 3. Средний квадрат отклонений, рассчитанный от средней величины, всегда будет меньше среднего квадрата отклонений, рассчитанного от любой другой величины А (свойство минимизации): Показатели вариации альтернативного признака Альтернативный признак –это качественный (атрибутивный) признак, который показывает наличие или отсутствие данного признака у единицы совокупности (да или нет). Среднее значение альтернативного признака:
где
Дисперсия альтернативного признака: Показатели вариации для сгруппированных признаков Общая дисперсия 
Внутригрупповая (случайная) дисперсия где По всем группам рассчитывают среднюю внутригрупповую дисперсию
где Межгрупповая (систематическая) дисперсия
где Все три вида дисперсии связанны Законом сложения дисперсий – общая дисперсия всегда равна сумме средней внутригрупповой и межгрупповой дисперсий: Для характеристики влияния группировочного признака на общую вариацию рассчитывают корреляционное отношение Чем больше корреляционное отношение, тем больше фактор, положенный в основание группировки, оказывает влияние на общую вариацию. Моменты распределения Моменты распределения –обобщающая характеристика, определяющая характер распределения. Данное понятие взято из механики. Моментом Моменты, в зависимости от величины · начальные; · начальные относительно · центральные. Начальные моментырассчитывают, подставляя в предыдущую формулу В практике статистики применяют следующие начальные моменты: · нулевого порядка: · первого порядка: · второго порядка: · третьего порядка: · четвертого порядка: Условные моменты получают при В практике статистики применяют следующие условные моменты: · первого порядка: · второго порядка: · третьего порядка: · четвертого порядка: Центральные моменты получают, когда В практике статистики применяют следующие центральные моменты: · нулевого порядка: · первого порядка: · второго порядка: · третьего порядка: · четвертого порядка: На практике используются только центральные моменты третьего порядка для определения показателя асимметрии и четвертого порядка для определения показателя эксцесса. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 264. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . Отсюда следует, что дисперсию можно рассчитать не только по заданным вариантам, но и по отклонениям этих вариант от какого-то постоянного числа:
. Отсюда следует, что дисперсию можно рассчитать не только по заданным вариантам, но и по отклонениям этих вариант от какого-то постоянного числа:  .
. . Отсюда следует, что все варианты можно разделить на какое-то одно и то же постоянное число (например, интервал ряда), рассчитать среднее квадратическое отклонение, а затем умножить его на это постоянное число:
. Отсюда следует, что все варианты можно разделить на какое-то одно и то же постоянное число (например, интервал ряда), рассчитать среднее квадратическое отклонение, а затем умножить его на это постоянное число: 
 .
.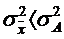 , причем больше на квадрат разности между средней
, причем больше на квадрат разности между средней  и этой величиной А, т.е. на
и этой величиной А, т.е. на  . Данное правило можно записать как
. Данное правило можно записать как  или
или  .
. ,
, – доля единиц совокупности, обладающая альтернативным признаком;
– доля единиц совокупности, обладающая альтернативным признаком;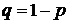 – доля единиц совокупности, не обладающая альтернативным признаком, а
– доля единиц совокупности, не обладающая альтернативным признаком, а  .
. .
. показывает величину вариации во всей совокупности, сложившуюся под влиянием всех факторов:
показывает величину вариации во всей совокупности, сложившуюся под влиянием всех факторов: – простая;
– простая;  – взвешенная.
– взвешенная. показывает величину вариации внутри групп, на которые разбита совокупность, обусловленная случайными причинами:
показывает величину вариации внутри групп, на которые разбита совокупность, обусловленная случайными причинами: – простая;
– простая;  – взвешенная,
– взвешенная, – групповая средняя.
– групповая средняя.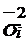 :
: – простая;
– простая;  – взвешенная,
– взвешенная, – общая численность по всем группам;
– общая численность по всем группам; показывает величину вариации групповых средних относительно общей средней, обусловлена систематическими причинами.
показывает величину вариации групповых средних относительно общей средней, обусловлена систематическими причинами. – простая;
– простая;  – взвешенная,
– взвешенная, – число групп.
– число групп. .
.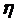 :
:  .
. -го порядка называется средняя из
-го порядка называется средняя из  от некоторой величины
от некоторой величины  –
– 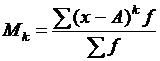 .
. ;
;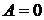 :
:  .
. ;
; ;
; ;
; ;
; .
. .
.
 ;
; ;
; .
. .
. ;
; ;
; ;
; ;
; .
.