
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение №1.1 («по-взрослому»). ⇐ ПредыдущаяСтр 5 из 5 Минимизировать время выплат можно, только максимизировав сами выплаты. Решим задачу в общем виде. Пусть
После предпоследней выплаты останется Относительно
По условию Так как Ответ: 4. Решение №1.2 («по-детски»). Если бы банк не брал процентов, то долг можно было бы вернуть за 3 месяца. Банк за 3 месяца возьмет меньше, чем 3% от первоначальной суммы в 900 тыс., т.е. меньше 27 тыс. Поэтому то, что забирает банк, точно можно будет оплатить в 4-й месяц, потратив меньше 300 тыс. Ответ: 4. Задача 2. 15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита? Решение. Пусть 15-го числа текущего месяца долг равен Значит, в процентах от суммы кредита выплаты в феврале составили  Ответ: 22,5.
Задача 3. В июле планируется взять кредит в банке на сумму 28 млн рублей — каждый январь долг возрастает на 25% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 9 млн рублей? Решение 1.Пусть кредит планируется взять на 28, По условию, каждый январь долг возрастает на 25%, значит, последовательность размеров долга (в млн рублей) в январе такова: 35, Следовательно, выплаты (в млн рублей) должны быть следующими:
Получаем:
Ответ: 80,5 млн рублей.
Решение 2.По условию долг уменьшается по арифметической прогрессии:
Первая выплата равна Общая выплата равна Ответ: 80,5 млн рублей.
Примеры оценивания решений заданий 17 Пример 1. 1 июня 2013 года Всеволод Ярославович взял в банке 900 000 рублей в кредит. Схема выплаты кредита следующая – 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Всеволод Ярославович переводит в банк платёж. На какое минимальное количество месяцев Всеволод Ярославович может взять кредит, чтобы ежемесячные выплаты были не более 300 000 рублей? Ответ:4.
Комментарий. Ответ верен. Более того «…построена математическая модель, решение сведено к исследованию этой модели…», см. критерии; в данном случае – арифметическая, числовая модель. Однако, эта модель построена неверно, т.е. она не соответствует условию. По решению видно, что сначала идет платёж долга, потом – начисление процента, а в условии – наоборот. Оценка эксперта: 0 баллов. Пример 2. 1 июня 2013 года Всеволод Ярославович взял в банке 900 000 рублей в кредит. Схема выплаты кредита следующая – 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Всеволод Ярославович переводит в банк платёж. На какое минимальное количество месяцев Всеволод Ярославович может взять кредит, чтобы ежемесячные выплаты были не более 300 000 рублей? Ответ:4.
Комментарий. Здесь и ответ верен, и движение денег в целом описано верно. К сожалению, в вычислениях есть просчет в первой клетке третьей строки. Добавлен не 1%, а 10%. Эта ошибка «играет» в пользу писавшего, но вычислительная ошибка имеется. Работает критерий на 2 балла, если в «недостаточно обосновано» включить и случай обоснования с вычислительной ошибкой. Оценка эксперта: 2 балла. Пример 3. 15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита? Ответ:22,5.
Комментарий. Почти правильное решение. Есть один обидный (по невнимательности?) прокол: перед выплатой в июле оставшаяся половина долга также увеличивается на 5% Оценка эксперта: 2 балла. Пример 4.См. задача 3. Кредит = 28 млн рублей. Рост на 25%. Выплаты равномерные, наибольший платеж 9 млн. Чему будет равна общая сумма выплат после полного погашения кредита? Ответ: 80,5 млн рублей.
Комментарий. На беглый взгляд – просто вычислительная ошибка, т.е. 2 балла. Смотрим внимательнее. Первые 4 строки заполнены с пониманием дела, разве что нет обоснования того, что именно первая выплата – наибольшая. В целом, верно описана процедура движения финансов: уменьшение долга, уменьшение размеров выплат. Но, судя по первому столбцу, строчек должно быть 14 (кредит взяли на 14 лет), а у автора, судя по последнему столбцу, их 18. К тому же, есть ошибка в подсчете: 9,5х9 явно больше 75,5. Оценка эксперта: 1 балл. Пример 5. См. задача 3. Кредит =9 млн . Рост на 10%. Выплаты равномерные, наибольший платеж 1,5 млн. Чему будет равна общая сумма выплат после полного погашения кредита? Ответ: 16,2 млн рублей.
Комментарий.Полная и верная бухгалтерская выписка. Можно попробовать «придраться»: а почему именно первая выплата – наибольшая. Но вряд ли возможно снять 1 балл только за это: ведь реализуемость всех условий представлена. Оценка эксперта: 3 балла. Ответ: 26,35 млн рублей.
Комментарий.По внешнему виду – почти то же, что и в Примере 5. Но тут принципиальное непонимание условия: всё время вычитается по 3,4 млн., а в конце – получившийся остаток, меньший 3,4 млн. Скорее всего, автор «переготовился» к ЕГЭ по другой модели «экономической» задачи, с так называемыми «аннуитентными» выплатами.
Оценка эксперта: 0 баллов. Критерии проверки и оценка решений заданий 18 (20 в 2015 г., С5 ранее) вариантов КИМ ЕГЭ–2017
Как это обычно бывает, задачи с параметром допускают весьма разнообразные способы решения. Наиболее распространенными из них являются: – чисто алгебраический способ решения; – способ решения, основанный на построении и исследовании геометрической модели данной задачи; – функциональный способ, в котором могут быть и алгебраические, и геометрические моменты, но базовым является исследование некоторой функции. Зачастую (но далеко не всегда) графический метод более ясно ведёт к цели. Кроме того, в конкретном тексте решения вполне могут встречаться элементы каждого из трех перечисленных способов. Ниже приведены задачи двух типов из материалов досрочного и основного ЕГЭ–2015, их решения, ответы и соответствующие критерии проверки. Далее в Части 1 приведены 6 примеров решений этих задач на ЕГЭ вместе с комментариями по оценке и самими оценками. Подчеркнём, что каждая задача оценивалась по критериям соответствующего года проведения ЕГЭ.
Задачи типа 1 и 2 имеют много схожего в своей структуре и условиях: (1) это системы относительно двух переменных; (2) это системы с параметром; (3) первое уравнение системы довольно громоздкое, но не содержит параметр; (4) уравнение, содержащее параметр, напротив, весьма простое; это уравнение пучка параллельных прямых, или прямых, проходящих через фиксированную точку; (4) всё начинается с преобразований первого уравнения и его решения; (5) далее, как правило, удобнее использовать геометрическую интерпретацию; (6) верное выполнение (4) и (5) гарантирует получение 1 балла; (7) 3 балла выставляется за практически верное решение; допускаются только 1–2 неточности во включении концевых точек соответствующих промежутков; (8) оценка в 2 балла – самая редкая. В то же время, имеются и различия. В основном они связаны с видом первого уравнения. В заданиях первого типа эти уравнения сводятся к произведению двух линейных множителей или же линейного множителя и (простейшего) квадратичного множителя. Такое разложение можно провести или группировкой членов, или решая уравнение, как квадратное относительно одной из переменных. В заданиях второго типа присутствует модуль. При его раскрытии с помощью выделения полных квадратов всё сводится к дугам двух окружностей. Дальнейший существенный шаг состоит в нахождении угловых коэффициентов касательных в точках пересечения этих окружностей. Без знания того, что для наклонных прямых
Задача 1 Найдите все значения Решение. Решим первое уравнение:
Рассмотрим случай (1): Рассмотрим случай (2): Соберем сведения о числе решений в случаях (1) и (2) в таблице
Остается учесть те значения Ответ:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 сумма (в тыс. руб.) кредита;
сумма (в тыс. руб.) кредита;  задолженность в
задолженность в  й месяц;
й месяц;  – выплата в
– выплата в  ;
;  коэффициент ежемесячного повышения,
коэффициент ежемесячного повышения,  . Тогда
. Тогда
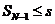 и тогда в последний,
и тогда в последний,  й раз, кредит будет погашен. Значит,
й раз, кредит будет погашен. Значит,  .
.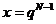 получаем неравенство
получаем неравенство .
. , т.е.
, т.е.  ,
, 
 , то
, то  .
. , а 15-го числа предыдущего месяца долг равен
, а 15-го числа предыдущего месяца долг равен  . Тогда в конце предыдущего месяца долг равен
. Тогда в конце предыдущего месяца долг равен 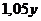 и поэтому выплата в первой половине текущего месяца равна
и поэтому выплата в первой половине текущего месяца равна  %, в марте составили
%, в марте составили  %, в апреле – 14%, в мае – 13,5%, в июне – 13%, а в июле
%, в апреле – 14%, в мае – 13,5%, в июне – 13%, а в июле  %. Следовательно, общая сумма выплат составила
%. Следовательно, общая сумма выплат составила 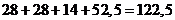 %.
%. лет. Долг перед банком (в млн рублей) по состоянию на июль должен уменьшаться до нуля равномерно:
лет. Долг перед банком (в млн рублей) по состоянию на июль должен уменьшаться до нуля равномерно: , …,
, …,  ,
,  , 0.
, 0. , …,
, …,  ,
, 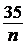 .
. ,
,  , …,
, …,  ,
,  .
. , откуда
, откуда  . Значит, всего следует выплатить
. Значит, всего следует выплатить (млн рублей).
(млн рублей). .
. . Вторая выплата равна
. Вторая выплата равна 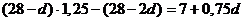 , третья равна
, третья равна 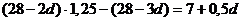 , четвертая равна
, четвертая равна  и т.д. Значит, наибольшая выплата – первая,
и т.д. Значит, наибольшая выплата – первая, 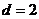 , выплат – 14 штук и они составляют арифметическую прогрессию, но с разностью
, выплат – 14 штук и они составляют арифметическую прогрессию, но с разностью  .
. .
.







 (или какого-то аналога нахождения уравнения перпендикуляра к заданной прямой в заданной точке) этот шаг становится почти непреодолимым. Судя по имеющимся сканам работ, верное нахождение угловых коэффициентов касательных в большинстве случаев гарантировало получение 3 баллов за решение.
(или какого-то аналога нахождения уравнения перпендикуляра к заданной прямой в заданной точке) этот шаг становится почти непреодолимым. Судя по имеющимся сканам работ, верное нахождение угловых коэффициентов касательных в большинстве случаев гарантировало получение 3 баллов за решение. , при каждом из которых система
, при каждом из которых система  имеет ровно два различных решения.
имеет ровно два различных решения.
 .
. . При любом
. При любом  получаем одно решение
получаем одно решение  , для которого неравенство
, для которого неравенство  верно только при
верно только при  .
. 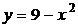 ,
, 
 . Так как
. Так как  , то при
, то при  корней нет, при
корней нет, при  получаем один корень
получаем один корень  , при
, при  получаем два различных корня. У параболы
получаем два различных корня. У параболы  - ветви вверх, абсцисса вершины равна
- ветви вверх, абсцисса вершины равна  и
и  . Значит, оба корня не меньше -3 при
. Значит, оба корня не меньше -3 при  т.е. при
т.е. при  , а при
, а при  один корень меньше -3, а другой – больше -3.
один корень меньше -3, а другой – больше -3.



 , и из
, и из  ,
,  .
. ,
,  .
.
 или
или