
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Последовательностей и рядов.Признак Вейерштрасса. Ф-циональную последовательность {fn)x)} x Î E наз. равномерно сходящейся ф-цией f на м-ж Е, если для Î e >0, сущ номер N, такой, что для " т х Î E и " n >N выполняется ¹-во: |fn(x)-f(x)|<e. Если м-ж {fn)x)} равномерно сходится на м-ж Е, то она и просто сходится в ф-ции f на сем м-ж. тогда пишут: fn à f.
Т. (Признак Вейерштрасса равномерной сходимости ряда) Если числовой ряд: где a >=0 сходится и для " x Î E и " n = 1,2… если выполняется нер-во |un(x)|<=an(8), ряд Док-вы: Абсолютная сходимость в каждой т. х следует из неравенства (8) и сходимости ряда (7). Пусть S(x) – сумма ряда (9), а Sn(x) – его частичная сумма. Зафиксируем произвольное e >0 В силу сходимости ряда (7) сущ. номера N, " n >N и вып. нерво Следовательно: |S(x)-Sn(x)| = Это означает, что Sn(x) à S(x) что означает равномерную сходимость ряда.. №12 Замена переменных В тройном интеграле. Если ограниченная замкнутая область пространства V = f(x,y,z) взаимно однозначно отображается на область V’ пространства = (u,v,w) Если непрерывно дифференцируемы функции: x=x(u,v,w), y=y(u,v,w), z=z(u,v,w) и существует якобиан
то справедлива формула:
При переходе к цилиндрическим координатам, с вязанными с x,y,z формулами: x=rcosj, y=rsinj, z=z (0<=r<=+¥, 0<=j <= 2p, -¥<=z<=+¥)  Якобиан преобразования:
И поэтому в цилиндрических координатах переход осуществляется так:
При переходе к сферическим координатам: r? j q, связанными с z,y,z формулами x=rsinq×cosj, y=r sinqsinj, z=rcosq. (0<=r<=+¥, 0<=j <= 2p, 0<=q <=2p) Якобиан преобразования:
Т. е. |J|=r2×sinq. Итак, в сферических координатах сие будет:
2 Свойства равномерно Сходящихся рядов Т1 Если ф-ция un(x), где х Î Е непрерывна в т. х0 Î E и ряд Т2 (Об поюленном интегрировании ряда) Пусть сущ. ф-ция un(x) Î R и непрерывная на отр. [a,b] и ряд Т3 (о почленном дифференцировании ряда) Пусть сущ. ф-ция un(x) Î R и непрерывная на отр. [a,b] и ряд её производных S’(x)= В силу ф-л ы (8) последнее равенство можно записать: ( So ряд (7) можно почленно дифференцировать №13 Приложения Тройных интегралов Объем тела Масса тела: Моменты инерции тела относительно осей координат:
Момент инерции относительно начала координат:
Координаты центра масс:
Интегралы, стоящие в числителях выражают статические моменты тела: Myz, Mxz, Mxy относит коорд плоскостей oyz, oxz, oxy. Если тело однородное: r(М) = const, то из формул она убирается и оне упрощаются как в 2ных интегралах. |
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 237. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 наз. равномерно сходящимся рядом, если на м-ж Е равномерно сходится последовательность его частичной суммы. , т. ен. равномерная сходимость ряда означает:Sn(x) à f(x) Не всякий сходящийся ряд является равномерно сходящимся, но всякий равномерно сходящийся – есть сходящийся (не, вот это наверное лет 500 выдумывали.)
наз. равномерно сходящимся рядом, если на м-ж Е равномерно сходится последовательность его частичной суммы. , т. ен. равномерная сходимость ряда означает:Sn(x) à f(x) Не всякий сходящийся ряд является равномерно сходящимся, но всякий равномерно сходящийся – есть сходящийся (не, вот это наверное лет 500 выдумывали.)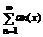 (7),
(7),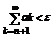


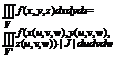


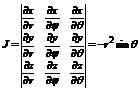

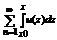 (4) тоже равномерно сходится на [a,b]. В частности: при x0 = a, х = b:
(4) тоже равномерно сходится на [a,b]. В частности: при x0 = a, х = b:  т. е. ряд (3) можно почленно интегрировать.
т. е. ряд (3) можно почленно интегрировать.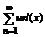 (6) равномерно сходящийся на отр [a,b] тогда, если ряд
(6) равномерно сходящийся на отр [a,b] тогда, если ряд 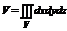
 , где r(М) = r(x,y,z) - плотность.
, где r(М) = r(x,y,z) - плотность.

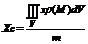

 m – масса.
m – масса.