
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Замена переменных в двойном интеграле.Общий случай криволинейных координат Пусть существует ф-ция f(x,y) интегр на области Д, можно прямолинейные координаты x, y с помощью формул преобразования перейти к криволинейным: x = x(u,v), y=y(u,v), где эти ф-ции непрерывные вместе с частными производными первого порядка, устанавливают взаимно однозначное и в обе стороны непрерывное соответствие между точками плоской области Д и области Д’ и определитель преобразования, наз. Якобианом не обращается в 0:
Интегральный признак Сходимости ряда. Ряд Дирихле Т1 Пущай дан рядт Если существует ф-ция f(x) неотрицательная, непрерывная и не возрастающая на [1,+¥] такая, что f(n) = Un, " n Î N, то для сходимости ряда (1) необходимо унд достаточно, чтобы сходился несобственный интеграл: Применим сей признак для исследования ряда Дирихле: Вот он: Возможны три случая: 1 a >1, Интеграл а потому и ряд сходится. 2 0<a<1,
Интеграл и ряд расходится 3 a=1,
Интеграл и ряд расходится № 6 Двойной интеграл В полярных координатах Переход к полярным координатам частный случай замены переменных.  Луч, проходящий из произв точки О имеет на плоскости полярные координаты A(r, j) где r = |ОA| расстояние от О до А полярный радиус. j = угол между векторами ОА и ОР – полярный угол отсчитываемой от полярной оси против часовой стрелки. всегда 0<=r<=+¥, 0<=j <=2p . Зависимость между прямоугольными и полярными координатами: x = r×cosj , y = r×sinj . Якобиан преобразования будет равен:
2 Признаки сравнения Т(Признаки сравнения) Пущай un<=vn (1)тогда 1 Если ряд vn сходится, то сходится и ряд un 2 если ряд un расходится, то расходится и ряд vn. Т. е. говоря простыми русскими словами для простых русских людей (ну для дураков вроде тебя): Из сходимости ряда с большими членами следует сходимость ряда с меньшими, а из расходимости ряда с меньшими членами следует расходимости ряда с большими и не наоборот!!! Причем можно требовать, чтобы неравенство (1) выполнялось не для всех номеров n, а начиная с некоторого n0, т. е. для некоторых номеров меньших n0 неравенство (1) может и не выполняться. При применении сего признака сравнения удобно в качестве ряда сравнения брать ряд Дирихле или геометрический ряд, с которыми и так уже все ясно. Т3 Засекреченная Если сущ вышеописанные неотр. ряды, то если сущ предел:
№7 Вычисление Площади плоской области С помощью 2ного интеграла Если Д правильная в направлении оу a<=x<=b, y1(x)<=y<=y2(x), то
Если Д огр линиями в полярных координатах, то
2 Признаки Даламбера и Коши Т(Признак Далембера) Пущай для ряда un с положит членами существует предел:
1 Если k<1, то ряд сходится 2 Если k>1 ряд расходится Т(Признак Коши) Пусть для того же самого ряда (т. е. положительного) существует предел: 1 Если k<1, то ряд сходится 2 Если k>1 ряд расходится А вот если эти все пределы по Коши и дедушке Даламберу равны 1, то о сходимости или расходимости ряда ничего сказать низзя. Вот низзя и все тут. Вот. №8 Вычисление объема С помощью 2ного интеграла Рассматривая в пространстве тело Р, огр снизу плоскостью оху, сверху z = f(x,y), кот проектируется в Д, сбоку границей области Д, называемое криволинейным цилиндром. Объем этого тела вычисляют по формуле: если f(x,y)<=0 в Д тор тело находится под плоскостью оху. Его объем равен объему цилиндрического тела. огр сверху ф-цией: z = |f(x,y)|>=0. тогда если в Д ф-ция меняет знак, то область разбивается на 2. Область Д1, f(x,y)>=0; Д2, f(x,y)<=0, тогда:
2 Знакочередующиеся ряды. Признак Лейбница. Ряд называется знакочередующимся если каждая пара соседних членов имеет разные знаки (один ♀, другой ♂), если считать каждый член сего ряда положительным то его можно записать в виде: Т (Признак Лейбница) Если для знакочередующегося ряды выполняются условия: 1) u1>=u2>=u3…>=un>=un+1… 2) то ряд сходится, а его сумма и остаток rn удовлетворяют неравенствам: 0<=S<=un и |rn|<=un+1 Ряд удовлетворяющий условиям теоремы наз. рядом Лейбница. Если условие чередования знаков выполняется не с первого члена, а с какого-нибудь исчо, то при существовании равного 0 предела ряд будет также сходится. №9 Вычисление Площади поверхности |
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 231. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 если это выполняется можно пользоваться ф-лой:
если это выполняется можно пользоваться ф-лой:
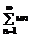 (1), члены которого неотрицательны, и не возрастают: u1>=u2>=u3…>=un
(1), члены которого неотрицательны, и не возрастают: u1>=u2>=u3…>=un , а для расходимости достаточно и необходимо чтобы сей интеграл наоборот расходился (ВАУ!).
, а для расходимости достаточно и необходимо чтобы сей интеграл наоборот расходился (ВАУ!).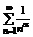 , a Î R Сей ряд называют обобщенным гармоническим рядом, при a >0 общий член оного un=1/na à0 и убывает поэтому можно воспользоваться интегральным признаком, функцией здеся будет ф-ция f(x)=1/xa (x>=1)сия ф-ция удовлетворяет условиям теоремы 1 поэтому сходимость (расходимости) ряда Дирихле равнозначна сходимости расходимости интеграла:
, a Î R Сей ряд называют обобщенным гармоническим рядом, при a >0 общий член оного un=1/na à0 и убывает поэтому можно воспользоваться интегральным признаком, функцией здеся будет ф-ция f(x)=1/xa (x>=1)сия ф-ция удовлетворяет условиям теоремы 1 поэтому сходимость (расходимости) ряда Дирихле равнозначна сходимости расходимости интеграла: 



 И формула при переходе примет вид:
И формула при переходе примет вид:
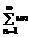 и
и  ряды с неотрицательными членами и для любого n выполняется нер-во:
ряды с неотрицательными членами и для любого n выполняется нер-во: (0<k<+¥) тада оба эти ряда сходятся.
(0<k<+¥) тада оба эти ряда сходятся.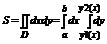

 , то
, то , тогда
, тогда



