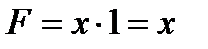Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
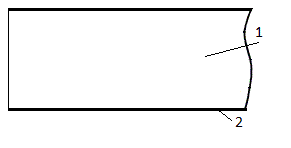
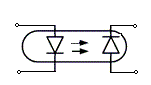
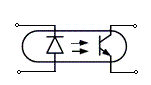
Световоды и простейшие оптроныМежду источником излучения и фотоприёмником имеется среда, которая выполняет функции световода. Для уменьшения потерь на отражение от границы разряда светоизлучателя и световода, последний должен иметь большой коэффициент преломления, так как соответствующий коэффициент преломления материалов, из которых изготавливают источники света обычно велик. В качестве материала световода используют свинцовые стёкла с n =1,7-1,9 и селеновые стёкла с n =2,4-2,6, где n – коэффициент преломления. Оптрон с селеновым световодом показан на рисунок 7.10, где 1 – инжекционный светодиод из арсенида галлия; 2 – световод из селенового стекла; 3 – кремниевый фотодиод. рисунок 7.10 В оптоэлектронике применяется волоконная оптика, которая во многих случаях имеет и самостоятельное значение. Работа элементов волоконной оптики основана на том, что свет передаётся по отдельному тонкому волокну, не выходя за его пределы вследствие полного внутреннего отражения. Собранные в один жгут волокна передают световые лучи независимо друг от друга. рисунок 7.11 Световод волоконной оптики (рисунок 7.11) состоит из сердечника 1 и отражающего покрытия 2. В таком волокне малого диаметра свет проходит не выходя за поверхность волокна, если угол изгиба меньше 90о. Световоды вносят некоторое запаздывание в передачу сигнала, которое на длине 1м составляет 10-9 – 10-10с. Материалами для волоконных световодов служат различные стёкла, как органические, так и неорганические.  Для интегральных оптоэлектронных микросхем применяются плёночные световоды. Они выполняются в виде плёночных полосок стекла толщиной 0,5 мкм и шириной 1-3 мкм. Источник света, световод и фотоприёмник вместе образуют оптрон. 1. Диодный оптрон (рисунок 7.12). рисунок 7.12 Источник света – светодиод из арсенида галлия. Фотоприёмник – кремневый фотодиод. Частота коммутации тока – 106 – 107 Гц. Сопротивление в закрытом состоянии 108 – 1010 Ом. Сопротивление в открытом состоянии 100 Ом – 10 кОм. 2. Транзисторный оптрон (рисунок 7.13).
рисунок 7.13
Имеет большую чувствительность в сравнении с диодными оптронами. Частота коммутации – 105 Гц. R закр. - 106 – 108 Ом. R откр. - 10 – 100 Ом. 3. Тиристорный оптрон (рисунок 7.14).
рисунок 7.14 Имеет большой выходной ток I вых. до 5А. I вх. до 10м. Время включения t вкл=10-5 с. Применяется в сильноточных цепях. 4. Резисторный оптрон (рисунок 7.15). рисунок 7.15 Применяется для различного рода бесконтактных регулировок в цепях автоматического управления. Излучатель – светодиод на основе фосфида галлия или электролюминесцентной конденсатор. Фотоприемник – пленочный фоторезистор. R закр. – 107 – 109 Ом. R откр. – 100 Ом ÷ 10 кОм. f до 10 кГц.
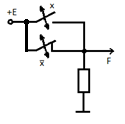
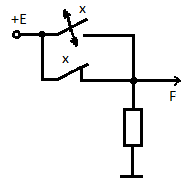
Цифровая техника В настоящее время для построения систем обработки и преобразования информации широко применяются цифровые методы. Используемые при этом сигналы близки по форме к прямоугольным и имеют два фиксированных уровня напряжения. Уровню низкого напряжения обычно приписывается символ (состояние) «0», а уровню высокого напряжения символ «1». Математическим аппаратом анализа и синтеза цифровых систем служит алгебра логики (булева алгебра), которая изучает связь между переменными (сигналами), принимающими только два значения «0» и «1». Алгебра логики является алгеброй состояний, а не алгеброй чисел, и для нее характерны основные действия, отличные от принятых в обычной алгебре действий над числами. 8.1.Аксиомы, законы, тождества и теоремы алгебры логики В алгебре логики любая переменная может иметь состояние «0» или «1». Поэтому в алгебре логики каждой двоичной переменной, например х, ставится в соответствие обратная или инверсная переменная Например: если х = 0, то Переменная В алгебре логики в случае одной переменной х действуют следующие правила (аксиомы) 1) х + 0 = х 2) х + 1 + 1 3) х + х = х 4) х + 5) ( 9) х · Правила 1 ÷ 4 характеризует операцию логического сложения (дизъюнкции), правила 6 ÷ 9 – операцию логического умножения (конъюнкции) и правила 5, 10 – операцию инверсии. Знак логического сложения «+» читается ИЛИ (например, правило 1 : «х» или «0» равен «х»). Знак логического умножения читается И (например «х» и «0» равен «0»). Правила 1-4 и 6-9 можно пояснить электрическими схемами на двух ключах. Положению « Ключ замкнут» соответствует состояние «1», а положению «Ключ разомкнут» - состояние «0». Для логического сложения (правила 1-4) ключи в схемах соединены параллельно (рисунок 8.1). Уровень высокого напряжения на выходе (F=1) будет иметь место, если хотя бы один из ключей находится в состоянии «1».
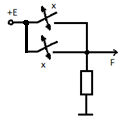
рисунок 8.1 Для логического умножения ключи в схемах соединены последовательно (рисунок 8.2). Уровень высокого напряжения на выходе F=1 будет только в том случае, если оба сомножителя равны единице (оба ключа включены). В противном случае результат умножения равен «0».
рисунок 8.2
Для алгебры логики, как и для обычной алгебры действительны следующие законы: Переместительный закон (закон коммутативности) для логического сложения и умножения: х + у = у + х х · у = у · х Сочетательный закон (закон ассоциативности) для логического сложения и умножения: х + у + z = (х + у) + z = х + (у + z) х · у · z = (x · y) z = x (y · z) Распределительный закон (закон дистрибутивности и логического умножения по отношению к сложению): х (y + z) = xy + xz Законы инверсии для логического сложения и умножения (теоремы де Моргана) Инверсия суммы переменных есть произведение их инверсий: Инверсия произведения переменных есть сумма их инверсий:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 628. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



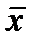 .
. = 1; если х = 1, то
= 1; если х = 1, то  ) = х
) = х