
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Обусловленность вычислительной задачиСледует понимать, что погрешность решения корректной задачи может быть как угодно мала только теоретически и только тогда, когда ИД могут быть заданы с адекватной точностью. На практике почти всегда невозможно задать ИД как угодно точно. Возникает проблема количественной оценки влияния погрешности ИД на погрешность решения — исследование обусловленности задачи. Под обусловленностью вычислительной задачи понимают чувствительность ее решения к малым погрешностям ИД. Задача хорошо обусловлена, если малым погрешностям ИД отвечают малые погрешности решения, и плохо обусловленной, если возможны сильные изменения решения. Количественной мерой степени обусловленности задачи является число обусловленности. Сформулируем эти положения точнее: если существует такое положительное число При каких значениях Пример хорошо и плохо обусловленных вычислительных задач классической корректной задачи
Т.е. при a = 1 имеем Dx*=1×Db, а при a = 0.001 имеем Dx*=103×Db. Пример Дж. Уилкинсона Рассмотрим задачу о вычислении корней многочлена 20-й степени В качестве многочлена 20-й степени возьмем простой многочлен Очевидно, что решение задачи  Предположим, что исходные данные — коэффициенты многочлена, содержат погрешности. Рассматриваемая задача плохо обусловлена, если малые погрешности исходные данных приводят к большим погрешностям решения (решение — корни многочлена). Уилкинсон рассмотрел пример, когда коэффициент многочлена Вычислим корни возмущенного многочлена
Т.е. если Видно, что первые шесть корней оказались практически нечувствительными к возмущению исходных данных, их погрешность не превышает Пример Дж.Уилкинсона — классический пример плохо обусловленной вычислительной задачи. Степень рассмотренного многочлена довольно велика. Однако плохо обусловленной может быть и задача о вычислении корней многочленов невысоких степеней. Рассмотрим задачу о вычислении корней многочлена 4-й степени |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 393. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , что имеет место неравенство
, что имеет место неравенство  , то число
, то число 
 ,
,  ,
,  ,
,  ,
, 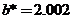 ,
, 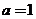 и
и  :
:

 .
. .
. существует и единственно: x1 = 1, x2 = 2, …, x20 = 20. Доказано, что эта задача устойчива относительно возмущения исходных данных (коэффициентов). Т.е. задача корректна.
существует и единственно: x1 = 1, x2 = 2, …, x20 = 20. Доказано, что эта задача устойчива относительно возмущения исходных данных (коэффициентов). Т.е. задача корректна. при
при 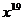 ,
,  , содержит малую ошибку:
, содержит малую ошибку:  .
. высокоточным алгоритмом и посмотрим, как столь незначительная погрешность влияет на значения корней?
высокоточным алгоритмом и посмотрим, как столь незначительная погрешность влияет на значения корней?


 — решение задачи P(x)=0, a
— решение задачи P(x)=0, a  — решение задачи P*(x)=0, погрешность исходных
— решение задачи P*(x)=0, погрешность исходных  и
и  , то
, то  . Задача плохо обусловлена.
. Задача плохо обусловлена. ; погрешности последующих корней растут, причем относительные погрешности некоторых корней приближаются к 20%.
; погрешности последующих корней растут, причем относительные погрешности некоторых корней приближаются к 20%. и соответствующую возмущенную задачу
и соответствующую возмущенную задачу  . (свободный член дан с относительной погрешностью
. (свободный член дан с относительной погрешностью  . Корни возмущенного многочлена
. Корни возмущенного многочлена  и
и  , их относительная погрешность
, их относительная погрешность  — задача плохо обусловлена.
— задача плохо обусловлена.