
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
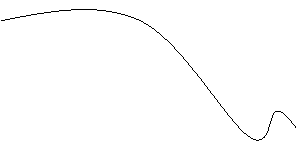
Основные методы решения многокритериальных задач оптимизацииЭта задача проектирования (оптимизации), в которых используется не один, а несколько критериев. На практике такие задачи возникают, когда проектируемый объект не может быть описан однокритериальной зависимостью, или объединить отдельные критерии в единый критерий не представляется возможным. Такое объединение, как правило, бывает формальным, искусственным. С математической точки зрения не существует идеального способа, метода решения многокритериальных задач оптимизации. Каждый из них имеет свои преимущества и недостатки. Рассмотрим некоторые методы решения этих задач. 1. Метод поиска Парето – эффективных решений. Рассмотрим его суть на примере использования двух критериев. Критерии при использовании данного метода являются равнозначными. Пусть имеется множество вариантов решения по каждому из вариантов определены значения всех критериев. Представим множество оценок вариантов решения в пространстве критериев на рисунке 4.
0
Рисунок 4. Иллюстрация поиска Парето-эффективных решений
На рисунке приняты следующие обозначения: К1 и К2 – критерий оценки вариантов решения; Y={y1, y2,…,ym} – множество оценок альтернативных вариантов решения; К11, К12,…,К1m – значения первого критерия для 1, 2,…, m-го варианта решения; К 21, К22,…,К2m – значения второго критерия для 1, 2,…,m-го варианта решения;  P(Y) – множество Парето-эффективных оценок решений Правило. Множество Парето-эффективных оценок P(Y) представляет собой «северо-восточную» границу множества Y без тех его частей, которые параллельны одной из координатных осей или лежат в «глубоких» провалах. Для случая изображенного на вышеуказанном рисунке, Парето-эффективные оценки состоят из точек кривой (bc), исключая точку (с), и линии (de). Преимущества метода: 1) критерии равнозначны; 2) метод математически объективен. Недостаток метода: 1) одно окончательное решение получается только в частном случае, т. е. количество Парето-эффективных решений, как правило, больше одного. 2. Метод решения многокритериальных задач оптимизации логистических систем с использованием обобщенного (интегрального) критерия. Суть данного метода заключается в том, что частные критерии - аддитивный критерий; - мультипликативный критерий; - максиминный (минимаксный) критерий. Аддитивный критерий. В них целевая функция получается путем сложения нормированных значений частных критериев. В общем виде целевая функция имеет следующий вид:
Где n – количество объединяемых частных критериев; С2 – весовой коэффициент i-го частного критерия; F2(X) – числовое значение i-го частного критерия; F Fi(X) – нормированное значение i-го частного критерия. Частные критерии имеют различную физическую природу и поэтому различную размерность. А значит просто суммировать их некорректно. В связи с этими в предыдущей формуле числовые значения критериев делятся на некоторые нормирующие делители, которые назначаются следующим образом: 1. В качестве нормирующих делителей принимаются директивные значения параметров или критериев, заданные заказчиком. Считается, что значения параметров, заложенные в техническом задании, являются оптимальными или 2. В качестве нормирующих делителей принимаются максимальные (минимальные) значения критериев, достигаемые в области допустимых решений. Размерность самих критериев и соответственно нормирующих делителей одинаковы, поэтому в итоге обобщенный адаптивный критерий получается безразмерной величиной. Преимущество данного метода: как правило, всегда удается определить единственный оптимальный вариант решения. Недостатки данного метода: - трудности (субъективизм) в определении весовых коэффициентов; - аддитивный критерий не вытекает из объектной роли частных критериев и поэтому выступает как формальный математический прием; - в аддитивном критерии происходит взаимная компенсация частных критериев, т. е. уменьшение одного из них может быть компенсировано увеличением другого критерия. Максиминный (минимаксный) критерий. Эти критерии работаю по принципу компромисса, который основывается на идее равномерности. Сущность принципа максимина заключается в следующем. При проектировании сложных систем, при наличии большого числа частных критериев установить между ними аналитическую взаимосвязь очень сложно. Поэтому стараются найти такие значения переменных критериев (параметров)
|
|||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 351. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
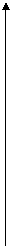
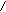
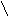
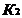 a b
a b





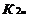
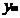 P(Y)
P(Y)
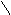
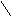
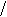








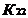
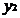 c d
c d




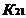
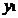

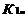
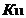
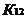
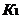

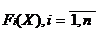 каким-либо образом объединяются в один интегральный критерий, а затем находятся максимум и минимум данного критерия. Но такое объединение осуществить крайне сложно различают или невозможно, поэтому, как правило, обобщенный частный критерий есть результат чисто формального объединения частных критериев. В зависимости от того, каким образом частные критерии объединяются в обобщенный критерий следующие виды обобщенных критериев:
каким-либо образом объединяются в один интегральный критерий, а затем находятся максимум и минимум данного критерия. Но такое объединение осуществить крайне сложно различают или невозможно, поэтому, как правило, обобщенный частный критерий есть результат чисто формального объединения частных критериев. В зависимости от того, каким образом частные критерии объединяются в обобщенный критерий следующие виды обобщенных критериев: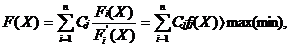
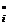 (X) – i-й нормирующий делитель;
(X) – i-й нормирующий делитель;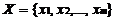 , при которых нормированные значения все частных критериев равны между собой. При большом количестве частных критериев из-за сложных взаимосвязей добиться выполнения указанного выше соотношения очень сложно. Поэтому на практике так варьируют значениями переменных проектирования, при которых последовательно «подтягиваются» те нормированные критерии, численные значения которых в исходном решении оказались наименьшими. Так как эта операция производится в области компромисса, подтягивание «отстающего» критерия неизбежно приводит к снижению значений части остальных критериев. Но при проведении ряда шагов можно добиться определенной степени уравновешивания противоречивых частных критериев, что является целью принципа максимина. Формально принцип максимина формулируется таким образом: выбрать такой набор переменных
, при которых нормированные значения все частных критериев равны между собой. При большом количестве частных критериев из-за сложных взаимосвязей добиться выполнения указанного выше соотношения очень сложно. Поэтому на практике так варьируют значениями переменных проектирования, при которых последовательно «подтягиваются» те нормированные критерии, численные значения которых в исходном решении оказались наименьшими. Так как эта операция производится в области компромисса, подтягивание «отстающего» критерия неизбежно приводит к снижению значений части остальных критериев. Но при проведении ряда шагов можно добиться определенной степени уравновешивания противоречивых частных критериев, что является целью принципа максимина. Формально принцип максимина формулируется таким образом: выбрать такой набор переменных 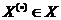 , при котором реализуется максимум из минимальных нормированных значений частных критериев, т.е.
, при котором реализуется максимум из минимальных нормированных значений частных критериев, т.е.  . Такой принцип выбора
. Такой принцип выбора 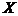 ° иногда носит название гарантированного результата. Он заимствован из теории игр, где является основным принципом. В этом случае применяются принцип минимакса:
° иногда носит название гарантированного результата. Он заимствован из теории игр, где является основным принципом. В этом случае применяются принцип минимакса: