
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Эллипсоиды, гиперболоиды и параболоидыОсновные определения, свойства и теоремы
Приведем канонические уравнения поверхностей второго порядка
Рис. 8 Рис. 12 Так как в уравнениях эллипсоидов и гиперболоидов переменные находятся только в четных степенях, то они симметричны относительно начала координат, координатных осей и координатных плоскостей. Форма поверхности второго порядка по ее уравнению изучается с помощью метода сечений, который состоит в следующем: пусть некоторая поверхность задана в прямоугольной системе координат своим общим уравнением. Данную поверхность пересекают плоскостями, параллельными координатным плоскостям (или самими координатными плоскостями), и находят линии пересечения поверхности с этими плоскостями. По виду этих линий и выносится суждение о форме рассматриваемой
Рис. 10 Рис. 11 Рис. 9 Определение. Прямая, лежащая на поверхности, называется прямолинейной образующей этой поверхности. Эллипсоид, двуполостный гиперболоид и эллиптический параболоид не имеют прямолинейных образующих. Однополостный гиперболоид
Пример решения задачи Написать уравнение двуполостного гиперболоида, проходящего через точки М1(3, 1, 2), М2(2,  Решение. Поскольку ось гиперболоида не задана, его уравнение представим Коэффициенты при
Таким образом, уравнение искомого двуполостного гиперболоида принимает вид
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 802. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 — эллипсоид (рис. 8);
— эллипсоид (рис. 8); — однополостный гиперболоид (рис. 9);
— однополостный гиперболоид (рис. 9); — двуполостный гиперболоид (рис. 10);
— двуполостный гиперболоид (рис. 10); — эллиптический параболоид (рис. 11);
— эллиптический параболоид (рис. 11); — гиперболический параболоид (рис. 12).
— гиперболический параболоид (рис. 12). ,3) и М3(6, 2,
,3) и М3(6, 2, 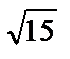 ), в канонической системе координат.
), в канонической системе координат. .
. обозначим соответственно через
обозначим соответственно через  , тогда
, тогда  .
.

 .
.