Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Взаимное расположение прямой и плоскостиСтр 1 из 4Следующая ⇒ Различные способы задания плоскости Основные определения, свойства и теоремы
В аналитической геометрии пользуются следующими способами задания плоскости. Определение. Вектор Уравнение плоскости, заданной точкой и двумя направляющими векторами. Пусть дана точка
2. Уравнение плоскости, заданной тремя точками. Пусть плоскость задана тремя точками
3. Уравнение плоскости, заданной точкой и нормальным вектором Определение. Вектор
Пусть в прямоугольной системе координат задана точка
Общее уравнение плоскости. Справедлива следующая теорема: Всякая плоскость в пространстве задается уравнением первой степени относительно переменных
Причем коэффициенты при переменных  5. Уравнение плоскости в «отрезках», отсекаемых на осях координат. Этот способ задания возможен, когда плоскость не проходит через начало координат и не параллельна координатным осям.
Числа Лемма о параллельности вектора плоскости. Пусть в аффинной системе координат задана плоскость π уравнением (4) и вектор
Примеры решения задач 1.Составить уравнение плоскости, проходящей через две данные различные точки Решение. Пусть Векторы
Таким образом, получено искомое уравнение плоскости.
2.Составить уравнение плоскости, проходящей через точку
Решение. По условию искомая плоскость перпендикулярна данным плоскостям, следовательно, она должна быть параллельна нормальным векторам этих плоскостей и проходить через точку М. На основании этого уравнение искомой плоскости будет иметь вид:
Взаимное расположение плоскостей. Расстояние Основные определения, свойства и теоремы
Пусть в аффинной системе координат даны две плоскости своими общими уравнениями: (1) Возможны следующие случаи: 1. Плоскости (1) и (2) совпадают-все коэффициенты 2. Плоскости (1) и (2) пересекаются, т. е. коэффициенты при соответствующих переменных в уравнениях плоскостей не пропорциональны. 3. Плоскости (1) и (2) параллельны, т. е. коэффициенты при соответствующих переменных в уравнениях плоскостей пропорциональны, но не пропорциональны свободные члены Следствие. Для того чтобы две плоскости, заданные в прямоугольной декартовой системе координат, были взаимно перпендикулярны, необходимо и достаточно, чтобы Определение.Пучком плоскостей,определяемым плоскостями (1) Уравнение произвольной плоскости пучка, определяемого пересекающимися плоскостями (1) и (2), имеет вид
Уравнение произвольной плоскости пучка параллельных плоскостей В прямоугольной декартовой системе координат расстояние от точки Определение.Углом j между двумя пересекающимися плоскостями называется любой из двух смежных двугранных углов, образованных этими плоскостями. Величина угла между плоскостями равна величине угла между нормальными векторами этих плоскостей В прямоугольной декартовой системе координат угол j вычисляется по формуле Примеры решения задач 1.Вывести формулу для вычисления расстояния между параллельными плоскостями π1:Ах+ Ву + Сz + D1 = 0 и π2: Ах+ Ву + Сz + D2 = 0, где Решение. Замечание: плоскости π1и π2 действительно параллельны, так как они перпендикулярны одному и тому же вектору Пусть Тогда р(π1, π2) = р(М0, π2), поэтому воспользуемся формулой расстояния от точки до плоскости Так как
Таким образом, искомая формула примет вид
2.Дан тетраэдр с вершинами Решение. Искомая высота равна расстоянию от точки D до плоскости, проходящей через точки А, В, С. Составим уравнение плоскости (ABC):
Вычислим по формуле расстояние от точки D до плоскости (ABC): Ответ: 4.
3.На осиОх найти точку, равноудаленную от точки Решение. Пусть Найдем расстояние от этой точки до данной плоскости и точки А:
Так как по условию Возведя в квадрат обе части последнего уравнения и приводя подобные члены, получим Следовательно, условию задачи удовлетворяют две точки
4.Составить уравнения плоскостей, делящих пополам двугранные углы между пересекающимися плоскостями
Решение. Каждая из искомых плоскостей является геометрическим местом
Так как по условию Откуда получаем уравнения искомых плоскостей:
В частности, если даны плоскости Следовательно, 1) 2) Различные способы задания прямой в пространстве. Основные определения, свойства и теоремы Приведем следующие способы задания и виды уравнений прямой 1. Канонические уравнения прямой, заданной точкой и направляющим вектором. Пусть d — прямая в пространстве, 2. Параметрические уравнения прямой, заданной точкой и направляющим вектором. Так как векторы 3. Уравнения прямой, заданной как линия пересечения двух плоскостей. Пусть прямая d является линией пересечения плоскостей При этом направляющий вектор прямой имеет вид 4. Канонические уравнения прямой, заданной двумя точками. Пусть в пространстве выбрана аффинная система координат, и в ней известны координаты двух точек Взаимное расположение прямых 1. Прямые 2. Прямые 3. Прямые 4. Прямые Взаимное расположение прямой и плоскости Пусть в пространстве дана прямая 1. Прямаяdпересекает плоскость π тогда и только тогда, когда направляющий вектор прямой не параллелен плоскости, т. е. когда Чтобы найти координаты точки пересечения прямой и плоскости, надо решить систему, состоящую из уравнений прямой и уравнения плоскости. 2. Прямая dпараллельна плоскости π тогда и только тогда, когда точка
3. Аналогично, прямая dлежит в плоскости π тогда и только тогда, когда выполняются равенства
Примеры решения задач 1.Составить канонические уравнения прямой, заданной в аффинной системе координат как линия пересечения двух плоскостей
Решение. Сначала выберем какую-нибудь точку на данной прямой
Для этого придадим одной из переменных, например z, произвольное значение. Пусть Таким образом, мы нашли точку Итак, искомые канонические уравнения прямой d имеют вид:
2.Выяснить взаимное расположение двух прямых, заданных в аффинной системе координат каноническими уравнениями:
Решение. По уравнениям находим точки и направляющие векторы данных прямых:
Учитывая, что Значит, данные прямые лежат в одной плоскости. При этом координаты векторов Отсюда вывод: данные прямые пересекаются.
3.Выяснить взаимное расположение прямой и плоскости, заданных
Решение. По каноническим уравнениям прямой находим точку Следовательно, прямая и плоскость параллельны. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 578. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 называется направляющим вектором плоскости π, если он параллелен этой плоскости или лежит на ней.
называется направляющим вектором плоскости π, если он параллелен этой плоскости или лежит на ней. , принадлежащая плоскости π и два неколлинеарных вектора
, принадлежащая плоскости π и два неколлинеарных вектора  (
(  ) и
) и 
 , параллельные этой плоскости. В этом случае уравнение плоскости имеет вид:
, параллельные этой плоскости. В этом случае уравнение плоскости имеет вид: . (1)
. (1)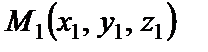 ,
, 
 , не лежащими на одной прямой. Тогда уравнение плоскости запишется в следующем виде:
, не лежащими на одной прямой. Тогда уравнение плоскости запишется в следующем виде: . (2)
. (2) называется вектором нормали (или нормальным вектором) плоскости π, если он перпендикулярен этой плоскости.
называется вектором нормали (или нормальным вектором) плоскости π, если он перпендикулярен этой плоскости. , принадлежащая плоскости π, и ненулевой вектор
, принадлежащая плоскости π, и ненулевой вектор 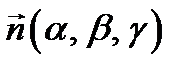 перпендикулярный этой плоскости. В этом случае уравнение плоскости имеет вид:
перпендикулярный этой плоскости. В этом случае уравнение плоскости имеет вид: . (3)
. (3)
 в аффинной системе координат есть уравнение плоскости.
в аффинной системе координат есть уравнение плоскости. — общее уравнение плоскости (4).
— общее уравнение плоскости (4). есть координаты вектора
есть координаты вектора  , перпендикулярного плоскости. Вектор
, перпендикулярного плоскости. Вектор  является нормальным вектором плоскости.
является нормальным вектором плоскости. . (5)
. (5) численно равны длинам отрезков, отсекаемых плоскостью на осях координат
численно равны длинам отрезков, отсекаемых плоскостью на осях координат  .
. . Для того чтобы вектор
. Для того чтобы вектор  был параллелен плоскости π, необходимо
был параллелен плоскости π, необходимо  .
. ,
,  параллельно данному вектору
параллельно данному вектору  . Векторы
. Векторы  и
и  неколлинеарны.
неколлинеарны. — произвольная точка плоскости.
— произвольная точка плоскости.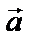 ,
,  ,
,  компланарны, поэтому их смешанное произведение равно нулю. В координатной форме это условие примет вид
компланарны, поэтому их смешанное произведение равно нулю. В координатной форме это условие примет вид .
. и перпендикулярной плоскостям:
и перпендикулярной плоскостям:

 .
. и (2)
и (2)  .
. .
. .
. .
. , где a и b принимают всевозможные значения, не равные одновременно нулю.
, где a и b принимают всевозможные значения, не равные одновременно нулю. , где l принимает всевозможные значения, причем
, где l принимает всевозможные значения, причем  — уравнение плоскости, определяющей пучок.
— уравнение плоскости, определяющей пучок. до плоскости π: Ах+ Ву + Сz + D = 0 вычисляется по формуле
до плоскости π: Ах+ Ву + Сz + D = 0 вычисляется по формуле  .
. .
. .
. .
. , но не совпадают
, но не совпадают  .
. — произвольная точка плоскости π1.
— произвольная точка плоскости π1. .
.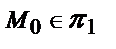 , то
, то  , следовательно
, следовательно .
. .
. ,
,  ,
,  ,
, 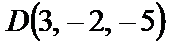 . Найти длину высоты, опущенной из вершины D на грань ABC.
. Найти длину высоты, опущенной из вершины D на грань ABC. ,
, или
или  .
. .
. и от плоскости
и от плоскости  .
. — искомая точка (
— искомая точка (  , так как точка лежит на осиОх).
, так как точка лежит на осиОх). ;
;  .
. , то
, то  или
или  .
. . Решением этого уравнения являются
. Решением этого уравнения являются  .
. и
и  .
.
 — произвольная точка искомой плоскости, тогда:
— произвольная точка искомой плоскости, тогда: ,
,  .
. , то
, то  .
. .
. ,
,  , то уравнения плоскостей, делящих пополам двугранные углы между ними, запишутся следующим образом:
, то уравнения плоскостей, делящих пополам двугранные углы между ними, запишутся следующим образом:  .
. .
. или
или 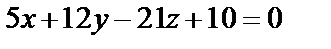 ;
; или
или  .
. — ее направляющий вектор,
— ее направляющий вектор,  — фиксированная точка этой прямой. Точка
— фиксированная точка этой прямой. Точка  лежит на прямой dтогда и только тогда, когда векторы
лежит на прямой dтогда и только тогда, когда векторы  и
и  коллинеарны. Условие коллинеарности векторов запишется в виде:
коллинеарны. Условие коллинеарности векторов запишется в виде:  . Эти равенства называются каноническими уравнениями прямойd.
. Эти равенства называются каноническими уравнениями прямойd. и
и  коллинеарны, то существует такое действительное число t, что
коллинеарны, то существует такое действительное число t, что  , тогда
, тогда  — параметрические уравненияпрямойd.
— параметрические уравненияпрямойd. и
и 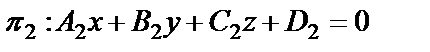 . Точка М(х, у,z) лежит на прямой dтогда и только тогда, когда ее координаты являются решением системы уравнений
. Точка М(х, у,z) лежит на прямой dтогда и только тогда, когда ее координаты являются решением системы уравнений  , поэтому эта система и является уравнениями прямойd.
, поэтому эта система и является уравнениями прямойd.
 и
и 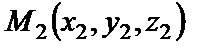 , принадлежащих прямой d, тогда канонические уравнения этой прямой примут вид
, принадлежащих прямой d, тогда канонические уравнения этой прямой примут вид  .
. и
и 
 и
и  скрещиваются (не лежат в одной плоскости) тогда и только тогда, когда векторы
скрещиваются (не лежат в одной плоскости) тогда и только тогда, когда векторы 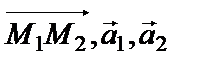 не являются компланарными, то есть их смешанное произведение
не являются компланарными, то есть их смешанное произведение  .
. и
и  пересекаются тогда и только тогда, когда векторы
пересекаются тогда и только тогда, когда векторы  являются компланарными, то есть
являются компланарными, то есть  , а векторы
, а векторы  и
и  не коллинеарны.
не коллинеарны.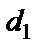 и
и  параллельны тогда и только тогда, когда векторы
параллельны тогда и только тогда, когда векторы  являются компланарными, то есть
являются компланарными, то есть  и
и  коллинеарны, но векторы
коллинеарны, но векторы  не коллинеарны.
не коллинеарны. и
и  совпадают тогда и только тогда, когда векторы
совпадают тогда и только тогда, когда векторы  являются коллинеарными.
являются коллинеарными. и плоскость
и плоскость 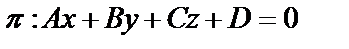 , причем
, причем  ,
,  .
.
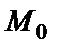 не лежит в этой плоскости и направляющий вектор прямой параллелен плоскости, т. е. выполняются соотношения
не лежит в этой плоскости и направляющий вектор прямой параллелен плоскости, т. е. выполняются соотношения

 и
и 

 , тогда из записанной выше системы
, тогда из записанной выше системы 
 , лежащую на данной прямой. Найдем координаты направляющего вектора прямой d:
, лежащую на данной прямой. Найдем координаты направляющего вектора прямой d:  или
или 
 .
.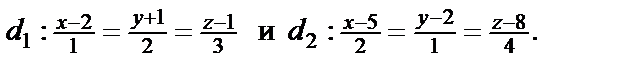


 , вычисляем смешанное произведение векторов
, вычисляем смешанное произведение векторов 
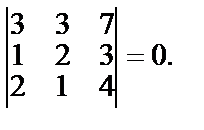
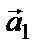 и
и  не пропорциональны, поэтому они не коллинеарны.
не пропорциональны, поэтому они не коллинеарны.
 на данной прямой и направляющий вектор
на данной прямой и направляющий вектор 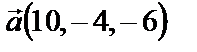 этой прямой. Имеем:
этой прямой. Имеем: