
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метрические задачи на сочетание прямых и плоскостейОсновные определения, свойства и теоремы
Задачи, содержащие метрические отношения: длины, расстояния, величины углов, площади и т. п., называются метрическими. Эти задачи удобно решать в прямоугольной системе координат. Для нахождения угла между прямыми используются их направляющие векторы (рис. 1), а для прямой и плоскости — направляющий вектор прямой и нормальный вектор плоскости (рис. 2).
Рис. 1 Рис. 2
Примеры решения задач 1.Выяснить взаимное расположение прямых, заданных в прямоугольной системе координат своими каноническими уравнениями: Решение. По каноническим уравнениям данных прямых находим координаты их направляющих векторов Выясним, пересекаются ли данные прямые или скрещиваются. Имеем на первой прямой точку Находим: Следовательно, данные прямые скрещиваются.
2.Вывести формулу для вычисления расстояния от точки Решение.
 , то , то  , где , где  — площадь параллелограмма, построенного на векторах — площадь параллелограмма, построенного на векторах  и и  (рис. 3). (рис. 3).
С другой стороны,
Таким образом,
Отсюда получаем формулу 3.Вывести формулу для вычисления расстояния между двумя скрещивающимися прямыми  Решение. Рассмотрим плоскость Рис. 4 Для нахождения этого расстояния построим параллелепипед
С другой стороны, Таким образом, Отсюда получаем формулу Кривые второго порядка Всякую кривую второго порядка можно описать уравнением вида:
где В зависимости от соотношения этих констант получаются уравнения окружности, эллипса или гиперболы. В частности, если
Если уравнение ( 1 ) разлагается на два линейных множителя, то оно определяет пару прямых, которые могут пересекаться, быть параллельными или совпадать. Определение Эллипсом Эти фиксированные точки плоскости называются фокусами эллипса.
Рис. 5. Эллипс
На рис. 5 обозначены:
Величина Директрисы – это прямые, параллельные малой оси и находящиеся от нее на расстоянии Каждое из расстояний от точки
Определение.Гиперболой
Точки, для которых выполняется условие Точки, для которых На рис.6 прямые Точки Эксцентриситет гиперболытакже вычисляется по формуле прямые
Виды гипербол: 1. Гипербола, у которой полуоси равны(a=b) называется равносторонней. 2. Гипербола с действительной осью ОУ,т.е. имеющая уравнение Определение Параболой
Элементами параболы являются:
уравнение директрисы
Фокус параболы 2. Парабола, с осью ОУ имеет уравнение: Фокус параболы 3. Парабола, с осью ОУ имеет уравнение: Фокус параболы
Примеры решения типовых задач: кривые второго порядка Задача 1 Найти центр и радиус окружности, заданной уравнением Решение: Приведем исходное уравнение к виду (2 ): выделим полные квадраты по
Ответ: координаты центра Задача 2. Найти координаты фокусов и эксцентриситет эллипса, описываемого уравнением Решение: 1. Приведем уравнение к виду (3): перепишем в виде:
2. Определяем расстояние фокусов от центра:
3. Эксцентриситет данного эллипса определяем по формуле:
Задача 3 Написать уравнение гиперболы, если ее фокусы находятся в точках Решение: 1. Для записи уравнения гиперболы в виде (4 ) необходимо знать величины 2. Из условия задачи можно определить величину 3. По формуле 4. Подставляем в уравнение ( 4 ), получаем Ответ: Задача 4 Вывести каноническое уравнение параболы, если известно, что ее вершина расположена в начале координат, она расположена симметрично оси Решение: 1. По условию парабола симметрична оси 2. Подставим в уравнение (.5 ) координаты точки, через которую проходит парабола: 3. Следовательно, уравнение параболы можно записать как Ответ: Приведение кривой к каноническому виду: Линии второго порядка-плоские линии, декартовы прямоугольные координаты которых удовлетворяют алгебраическому уравнению 2-й степени a11x2 + a12xy + a22y2 + 2a13x + 2a23y + a11 = 0. (*) Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую ЛВП. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса начала и поворота системы координат на некоторый угол к одному из 9 приведённых ниже канонических видов, каждому из которых соответствует определённый класс линий. Именно, нераспадающиеся линии:
x2 - а2 = 0 — пары параллельных прямых, x2 + а2 = 0 — пары мнимых параллельных прямых, x2 = 0 — пары совпадающих параллельных прямых!!!¿¿¿
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 579. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 и
и  . Вычислить угол между ними.
. Вычислить угол между ними. и
и  . Скалярное произведение этих векторов равно нулю, следовательно, данные прямые взаимно перпендикулярны.
. Скалярное произведение этих векторов равно нулю, следовательно, данные прямые взаимно перпендикулярны. и на второй прямой точку
и на второй прямой точку  . Эти точки определяют вектор
. Эти точки определяют вектор  .
.
 до прямой
до прямой  .
.


 =
=  .
.  .
. и
и  .
. , проходящую через прямую
, проходящую через прямую  параллельно прямой
параллельно прямой  , и плоскость
, и плоскость  , проходящую через прямую
, проходящую через прямую 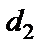 параллельно прямой
параллельно прямой  . Из школьного курса стереометрии известно, что такие плоскости существуют и определяются однозначно. Очевидно, что расстояние между прямыми
. Из школьного курса стереометрии известно, что такие плоскости существуют и определяются однозначно. Очевидно, что расстояние между прямыми  и
и  равно расстоянию между параллельными плоскостями
равно расстоянию между параллельными плоскостями  и
и  .
. так, как показано на рисунке (рис. 4), и обозначим через
так, как показано на рисунке (рис. 4), и обозначим через 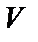 объем этого параллелепипеда. Известно, что
объем этого параллелепипеда. Известно, что .
. .
.
 .
. .
.  ,
,
 – константы.
– константы. и
и  , уравнение ( 1 ) описывает уравнение окружности:
, уравнение ( 1 ) описывает уравнение окружности:  , или, выделив полный квадрат:
, или, выделив полный квадрат:
 ,
,
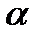 называется геометрическое место точек плоскости, для которых сумма расстояний до двух заданных точек плоскости, есть величина постоянная.равная
называется геометрическое место точек плоскости, для которых сумма расстояний до двух заданных точек плоскости, есть величина постоянная.равная 














 – вершины эллипса;
– вершины эллипса; 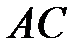 – большая ось
– большая ось  ;
;  – малая ось
– малая ось  ; а -большая полуось, b-малая полуось
; а -большая полуось, b-малая полуось и
и  – фокусы эллипса, лежащие на большой оси по обе стороны от центра на расстоянииc от него; причём
– фокусы эллипса, лежащие на большой оси по обе стороны от центра на расстоянииc от него; причём 
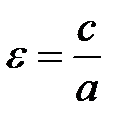 – называется эксцентриситетом эллипса
– называется эксцентриситетом эллипса 
 .
. до фокусов определяется по формулам:
до фокусов определяется по формулам:  ,
,  ,
,  .
.
 ,
,
 называется геометрическое место точек, для каждой из которых модуль разности расстояний до двух заданных точек (фокусов) есть величина постоянная, равная
называется геометрическое место точек, для каждой из которых модуль разности расстояний до двух заданных точек (фокусов) есть величина постоянная, равная 










 , принадлежат одной ветви гиперболы (на рис. 6 - правой).
, принадлежат одной ветви гиперболы (на рис. 6 - правой). принадлежат другой ветви гиперболы (на рис. 6 - левой).
принадлежат другой ветви гиперболы (на рис. 6 - левой). – действительная полуось,
– действительная полуось,  – мнимая полуось гиперболы;
– мнимая полуось гиперболы; – асимптоты гиперболы;
– асимптоты гиперболы;  и
и  - фокусы гиперболы.
- фокусы гиперболы. ,
,  называются вершинами гиперболы,причём
называются вершинами гиперболы,причём 

 ;
;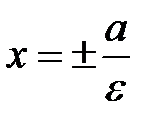 перпендикулярны к действительной оси и называются директрисами гиперболы.
перпендикулярны к действительной оси и называются директрисами гиперболы.
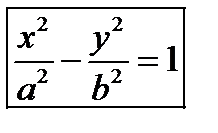 .
.
 называется сопряжённой для гиперболы
называется сопряжённой для гиперболы  . Такая гипербола пересекает ось ординат, асимптоты сопряженной гиперболы и гиперболы
. Такая гипербола пересекает ось ординат, асимптоты сопряженной гиперболы и гиперболы  совпадают.
совпадают. называется геометрическое место точек, равноудаленных от данной точки (фокуса) и от данной прямой (директрисы) плоскости.
называется геометрическое место точек, равноудаленных от данной точки (фокуса) и от данной прямой (директрисы) плоскости. – ось параболы;
– ось параболы; – параметр параболы - расстояние между фокусом и директрисой;
– параметр параболы - расстояние между фокусом и директрисой; – вершина параболы;
– вершина параболы; – фокус параболы (точка, лежащая на расстоянии
– фокус параболы (точка, лежащая на расстоянии  от вершины);
от вершины);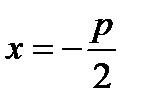 (рис. 7).
(рис. 7).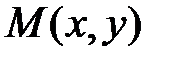

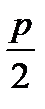



 .
Виды парабол:
1.Парабола, имеющая уравнение:
.
Виды парабол:
1.Парабола, имеющая уравнение:  называется сопряжённой для параболы
называется сопряжённой для параболы  .
.
 ; ветви направлены влево.
; ветви направлены влево.
 ; ветви направлены вверх
; ветви направлены вверх и называется сопряжённой для предыдущей параболы.
и называется сопряжённой для предыдущей параболы. ; ветви направлены вниз.
; ветви направлены вниз. .
. и
и  , для этого разобьем свободный член на элементы:
, для этого разобьем свободный член на элементы: , или
, или . Согласно уравнению (2 ) получаем
. Согласно уравнению (2 ) получаем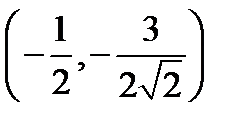 , радиус-
, радиус-  .
. .
. , откуда
, откуда  ,
,  .
. , то есть
, то есть  ,
,  .
. . Ответ:
. Ответ: 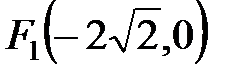 ,
, 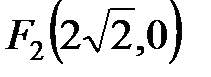 ,
, 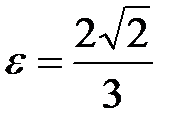 .
. ,
, 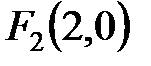 , а длина ее действительной полуоси равна 1.
, а длина ее действительной полуоси равна 1. и
и  . Величина
. Величина  по условию задачи (длина вещественной полуоси). Определим величину
по условию задачи (длина вещественной полуоси). Определим величину  .
. . Это первая координата фокуса, то есть
. Это первая координата фокуса, то есть  .
. определяем величину
определяем величину  :
: 
 .
. , и проходит через точку
, и проходит через точку  .
.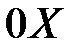 и вершина расположена в центре координат, следовательно, для нахождения параметра параболы можно воспользоваться каноническим уравнением (.5 ).
и вершина расположена в центре координат, следовательно, для нахождения параметра параболы можно воспользоваться каноническим уравнением (.5 ).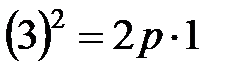 , откуда
, откуда  .
. .
.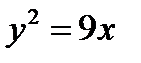 .
. эллипс
эллипс  гипербола y2 = 2px — парабола,
гипербола y2 = 2px — парабола, мнимый эллипс;
мнимый эллипс; — пары пересекающихся прямых,
— пары пересекающихся прямых, — пары мнимых пересекающихся прямых,
— пары мнимых пересекающихся прямых,