Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Интегрирование степенных рядов.Если некоторая функция f(x) определяется степенным рядом:
2) Дифференцирование степенных рядов.
Производная функции, которая определяется степенным рядом, находится по формуле:
3) Сложение, вычитание, умножение и деление степенных рядов.
Сложение и вычитание степенных рядов сводится к соответствующим операциям с их членами:
Произведение двух степенных рядов выражается формулой:
Коэффициенты сi находятся по формуле:
Делениедвух степенных рядов выражается формулой:
Для определения коэффициентов qn рассматриваем произведение
Разложение функций в степенные ряды.
Разложение функций в степенной ряд имеет большое значение для решения различных задач исследования функций, дифференцирования, интегрирования, решения дифференциальных уравнений, вычисления пределов, вычисления приближенных значений функции. Возможны различные способы разложения функции в степенной ряд. Такие способы как разложение при помощи рядов Тейлора и Маклорена были рассмотрены ранее. (См. Формула Тейлора. ) Существует также способ разложения в степенной ряд при помощи алгебраического деления. Это – самый простой способ разложения, однако, пригоден он только для разложения в ряд алгебраических дробей.
Пример. Разложить в ряд функцию Суть метода алгебраического деления состоит в применении общего правила деления многочленов:
 1 – x 1 + x + x2 + x3 + … x x – x2 x2 x2 – x3 x3 ……….
Если применить к той же функции формулу Маклорена
то получаем: ………………………………. Итого, получаем:
Рассмотрим способ разложения функции в ряд при помощи интегрирования.
С помощью интегрирования можно разлагать в ряд такую функцию, для которой известно или может быть легко найдено разложение в ряд ее производной. Находим дифференциал функции
Пример. Разложить в ряд функцию Разложение в ряд этой функции по формуле Маклорена было рассмотрено выше. (См. Функция y = ln(1 + x).) Теперь решим эту задачу при помощи интегрирования.
При
Разложение в ряд функции
Тогда получаем:
Окончательно получим:
Пример. Разложить в степенной ряд функцию Применим разложение в ряд с помощью интегрирования.
Подинтегральная функция может быть разложена в ряд методом алгебраического деления:
- x2 – x4
………….
Тогда
Окончательно получаем:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 479. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , то интеграл от этой функции можно записать в виде ряда:
, то интеграл от этой функции можно записать в виде ряда:
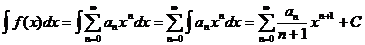


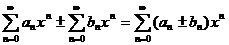



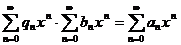 , полученное из записанного выше равенства и решаем систему уравнений:
, полученное из записанного выше равенства и решаем систему уравнений: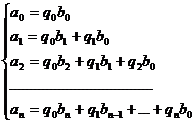
 .
. 1 1 - x
1 1 - x ,
,

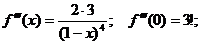


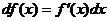 и интегрируем его в пределах от 0 до х.
и интегрируем его в пределах от 0 до х.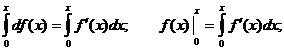


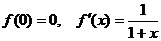 получаем по приведенной выше формуле:
получаем по приведенной выше формуле: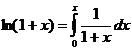
 может быть легко найдено способом алгебраического деления аналогично рассмотренному выше примеру.
может быть легко найдено способом алгебраического деления аналогично рассмотренному выше примеру.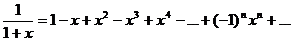



 .
.



 1 1 + x2
1 1 + x2 1 + x2 1 – x2 + x4- …
1 + x2 1 – x2 + x4- … - x2
- x2 x4
x4
 x4 + x6
x4 + x6