
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные однородные дифференциальные уравнения в частныхпроизводных первого порядка.
Дифференциальное уравнение в частных производных первого порядка от функции
Линейноеуравнение в частных производных имеет вид: где Xi – некоторые заданные функции.
Очевидно, что одним из решений такого уравнения будет функция u = C.
Рассмотрим систему уравнений: или Общее решение этой системы имеет вид:
Если разрешить эти уравнения относительно постоянных С, получим:
Каждая из функций j является интегралом системы (2).
Теорема. Если
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 479. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
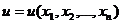 можно в общем виде записать как
можно в общем виде записать как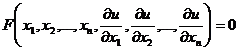
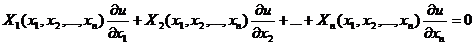 , (1)
, (1)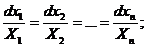 (2)
(2)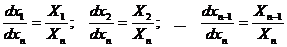 - такая система называется нормальной.
- такая система называется нормальной.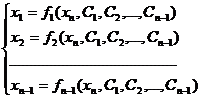
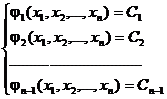
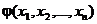 - интеграл системы (2), то функция
- интеграл системы (2), то функция 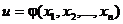 - решение уравнения (1).
- решение уравнения (1).