Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные однородные дифференциальные уравнения спроизвольными коэффициентами.
Рассмотрим уравнение вида
Определение. Выражение Линейный дифференциальный оператор обладает следующими свойствами:
1) 2)
Решения линейного однородного уравнения обладают следующими свойствами:
1) Если функция у1 является решением уравнения, то функция Су1, где С – постоянное число, также является его решением. 2) Если функции у1 и у2 являются решениями уравнения, то у1 +у2 также является его решением.
Структура общего решения.
Определение. Фундаментальной системой решенийлинейного однородного дифференциального уравнения n –го порядка на интервале (a, b) называется всякая система n линейно независимых на этом интервале решений уравнения.
Определение. Если из функций yi составить определитель n – го порядка
то этот определитель называется определителем Вронского. ( Юзеф Вроньский (1776 – 1853) – польский математик и философ - мистик)
Теорема. Если функции
Теорема. Если функции
Теорема. Для того, чтобы система решений линейного однородного дифференциального уравнения Теорема. Если 
где Ci –постоянные коэффициенты.
Применение приведенных выше свойств и теорем рассмотрим на примере линейных однородных дифференциальных уравнений второго порядка.
Общее решение линейного однородного дифференциального уравнения второго порядка.
Из вышеизложенного видно, что отыскание общего решения линейного однородного дифференциального уравнения сводится к нахождению его фундаментальной системы решений. Однако, даже для уравнения второго порядка, если коэффициенты р зависят от х, эта задача не может быть решена в общем виде. Тем не менее, если известно одно ненулевое частное решение, то задача может быть решена.
Теорема. Если задано уравнение вида
Таким образом, для получения общего решения надо подобрать какое – либо частное решение дифференциального уравнения, хотя это бывает часто довольно сложно.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 436. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
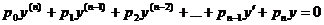
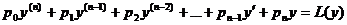 называется линейным дифференциальным оператором.
называется линейным дифференциальным оператором.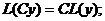
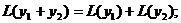
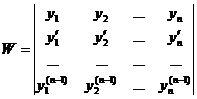 ,
,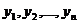 линейно зависимы, то составленный для них определитель Вронского равен нулю.
линейно зависимы, то составленный для них определитель Вронского равен нулю.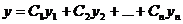 ,
,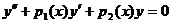 и известно одно ненулевое решение у = у1, то общее решение может быть найдено по формуле:
и известно одно ненулевое решение у = у1, то общее решение может быть найдено по формуле: