
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Потенциал электрического поля. Эквипотенциальные поверхности. ⇐ ПредыдущаяСтр 4 из 4 При изучении курса механики было показано, что центральные силы (силы которые зависят только от расстояния между частицами) являются потенциальными. Остановимся на вычислении потенциальной энергии взаимодействия двух зарядов. Рассмотрим перемещение частиц с зарядами
Эта работа совершается за счет убыли потенциальной энергии, (выше мы отмечали, что частицы имеют нулевую скорость). Это значит, что произведенная работа равна убыли потенциальной энергии:
Отсюда следует, что энергия взаимодействия двух зарядов равна:
Мы будем выбирать
Из этого выражения видно, что если пробный заряд не изменяет расположение зарядов создающих поле, то его энергия пропорциональна величине заряда. А энергия, численно равная энергии, которую имеет заряд 
Найдем связь между напряженностью и потенциалом поля. При изучении механики было показано, что сила равна минус градиенту от потенциальной энергии. Напишем это соотношение с учетом связи напряженности и потенциала с силой и энергией в электрическом поле:
Отсюда следует, что напряженность поля связана с потенциалом так же, как сила с потенциальной энергией:
И еще одно определение: «Поверхности, на которых потенциал остается постоянным:
называются эквипотенциальными».Вектор напряженности перпендикулярен к эквипотенциальным поверхностям. Рассмотрим эквипотенциальные поверхности некоторых заряженных систем, поле которых известно. 1. Потенциал бесконечной заряженной поверхности.Плотность поверхностного заряда данаиобозначим её
Работа электростатических сил по перемещению заряда
Что дает следующую интегральную связь между разностью потенциалов и напряженностью электрического поля:
Чтобы найти потенциал поля в данной точке, необходимо выбрать какую-то точку за начальную, и вычислять интеграл (39) всегда стартуя с этой точки (фактически это означает выбор константы в определении потенциальной энергии). В данном случае такую точку можно выбрать в начале координат. В таком случае потенциал в точке с радиус вектором
и эквипотенциальными поверхностями являются плоскости 2. Потенциал бесконечной заряженной нити (см. Рис.4) с линейной плотностью
Отсюда следует, что эквипотенциальными поверхностями являются круговые цилиндры с образующими параллельными заряженной нити эта заряженная нить проходит через центр цилиндра. 3. Потенциал заряженного шара.Будем рассматривать потенциал заряженного шара (заряд Очевидно, что такой же потенциал создает и точечный заряд Относительно эквипотенциальных поверхностей можно заметить следующее: 1. Вектор напряженности электрического поля совпадает с нормалью к эквипотенциальной поверхности. 2. При перемещении заряда по эквипотенциальной поверхности электростатические силы не производят работы. 3. Если распределение зарядов обладает симметрией, то эквипотенциальные поверхности обладают той же симметрией.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 586. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
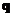 и
и  из положения (1) (с радиус-векторами
из положения (1) (с радиус-векторами  ) в положение (2)
) в положение (2)  . Считаем, что частицы перемещаются медленно, так что скорости их практически равны нулю и работа совершается за счет потенциальной энергии взаимодействия этих частиц. В курсе механики, когда мы рассматривали энергию системы взаимодействующих частиц, было показано, что при перемещении двух зарядов из положения (1) в положение (2) работа, совершаемая Кулоновскими силами равна:
. Считаем, что частицы перемещаются медленно, так что скорости их практически равны нулю и работа совершается за счет потенциальной энергии взаимодействия этих частиц. В курсе механики, когда мы рассматривали энергию системы взаимодействующих частиц, было показано, что при перемещении двух зарядов из положения (1) в положение (2) работа, совершаемая Кулоновскими силами равна:
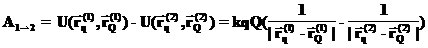

 . Остановимся на ситуации, когда пробный (не искажающий поле) заряд
. Остановимся на ситуации, когда пробный (не искажающий поле) заряд 
 , называется потенциалом электрического поля и обозначается
, называется потенциалом электрического поля и обозначается  (см. (32)). Размерность потенциала имеет свое название, которое вы много раз встречали в жизни, это Вольт (В) и дается следующим выражением через основные величины в системе СИ:
(см. (32)). Размерность потенциала имеет свое название, которое вы много раз встречали в жизни, это Вольт (В) и дается следующим выражением через основные величины в системе СИ: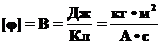 ,
,
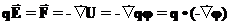

 ,
,
 . Выберем начало координат в какой-то точке на поверхности, Ось Z направим перпендикулярно поверхности. В этом случае плоскость (X,Y) совпадает заряженной поверхностью. Используя теорему Гаусса мы нашли, что в этом случае вектор напряженности электрического поля равен:
. Выберем начало координат в какой-то точке на поверхности, Ось Z направим перпендикулярно поверхности. В этом случае плоскость (X,Y) совпадает заряженной поверхностью. Используя теорему Гаусса мы нашли, что в этом случае вектор напряженности электрического поля равен: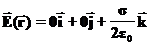 ,
,
 в точку (2)
в точку (2)  равна убыли потенциальной энергии:
равна убыли потенциальной энергии: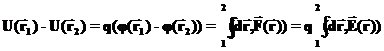 ,
,

 равен:
равен: ,
,

 . В этом случае удобно выбрать цилиндрическую систему координат с ось Z совпадающей с заряженной нитью. Выберем (1) на расстоянии
. В этом случае удобно выбрать цилиндрическую систему координат с ось Z совпадающей с заряженной нитью. Выберем (1) на расстоянии  от заряженной нити (координату
от заряженной нити (координату  можно выбрать любой) выберем на бесконечности, в таком случае потенциал находится из равенства:
можно выбрать любой) выберем на бесконечности, в таком случае потенциал находится из равенства: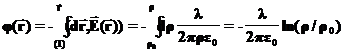 (41)
(41) ). Считаем, что заряд распределен по шару так, что его плотность зависит только от расстояния до центра шара. Точку (1) выберем на бесконечности и вычислим потенциал, пользуясь стандартным правилом:
). Считаем, что заряд распределен по шару так, что его плотность зависит только от расстояния до центра шара. Точку (1) выберем на бесконечности и вычислим потенциал, пользуясь стандартным правилом: (42)
(42)