
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Поток вектора через поверхность. Теорема Гаусса. Применение теоремы Гаусса для расчета электрических полей.Остановимся на понятие потока вектора. Терминология пришла из гидродинамики, науки описывающей движение жидкости. Если по трубе течет жидкость, то в каждой точке можно задать скорость, которая соответствует бесконечно малому элементу жидкости, находящемуся в данной точке. Рассмотрим самый простой случай, когда скорость во всех точках постоянна, а площадка (воображаемая) расположена перпендикулярно скорости течения жидкости (см. Рис.1). В таком случае за время
Рис.1
где
По определению получается, что масса жидкости, протекающая через наклонную площадку положительна, если нормаль к площадке совпадает с направлением нормали к поверхности, и отрицательна, если проекция нормали на скорость является отрицательной. А как быть, если скорость не постоянна, а поверхность имеет сложную форму? Математика говорит, что в этом случае нашу поверхность нужно разбить на много мелких плоских площадок так что:
Ну а масса жидкости, протекающей через сложной формы поверхность и в сложном поле скоростей в таком случае записывается в виде суммы потоков по всем площадкам: 
где
Из записи интеграла видно, что используется обозначение
Чаще нам придется использовать поток вектора через замкнутую поверхность, т.е. поверхность, ограничивающую некоторый объем. При этом будем считать, что нормаль к поверхности направлена наружу. Если вспомнить пример с несжимаемой жидкостью, то такое направление нормали (направление наружу) даст нам массу жидкости, которая вытекает из объема, ограниченного рассматриваемой поверхность в единицу времени.
Очевидно, что если в рассматриваемом объеме нет источников, то интеграл по поверхности должен быть равен нулю:
т.е. сколько жидкости втекает, сколько и вытекает (источников то нет). Ну а как обстоит дело с потоком вектора напряженности электрического поля? Для начала посчитаем поток напряженности электрического поля, создаваемого точечным зарядом, через сферическую поверхность с центром в месте расположения заряда. Это помимо прочего покажет нам, что в некоторых случаях интеграл по замкнутой поверхности посчитать не так уж и сложно. Итак: 1. Напряженность электрического поля создаваемая почечным зарядом, который мы поместим в начало координат равна (см. (9)):
2. И нужно вычислить интеграл:
где Для вычисления интеграла очень важно выбрать форму элементарных площадок, на которые мы разобьем нашу исходную сферу. Т.е. другими словами, какую систему координат мы выберем. Из симметрии нашей задачи, очевидно, что в нашем случае подходит сферическая система координат. Вам известно, что в этой системе координат положение почки задается расстоянием до начала координат
Получился интересный ответ, из которого видно, что интеграл не зависит от радиуса сферы, а зависит только от величины заряда, который внутри этой сферы находится. Больше того, можно доказать (мы этого делать не будем, хотя это и не сложно), что величина интеграла те зависит от формы поверхности. Таким образом, для любой замкнутой поверхности, внутри которой находится заряд
Ну а если зарядов внутри поверхности несколько? Ответ очевиден. Согласно принципу суперпозиции напряженность поля от этих зарядов равна сумме напряженности создаваемой каждым зарядом (см. (9))
Таким образом, мы получили, что интеграл по замкнутой поверхности от напряженности электрического поля равен заряду
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 533. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 через площадку протечет масса жидкости равная
через площадку протечет масса жидкости равная 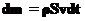 . Здесь
. Здесь  — плотность жидкости, которая считается постоянной. Таким образом, для массы, протекающей через нашу площадку в единицу времени получаем:
— плотность жидкости, которая считается постоянной. Таким образом, для массы, протекающей через нашу площадку в единицу времени получаем: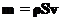

 , а масса жидкости, протекающая через наклоненную поверхность равна:
, а масса жидкости, протекающая через наклоненную поверхность равна: ,
,
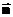 — нормаль к площадке.
— нормаль к площадке.
 ,
,
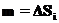 — площадь i-ой площадки,
— площадь i-ой площадки,  и
и  — нормаль, проведенная к i-ой площадке и скорость жидкость вблизи этой площадке. Заметьте, что при рассмотрении мы считали
— нормаль, проведенная к i-ой площадке и скорость жидкость вблизи этой площадке. Заметьте, что при рассмотрении мы считали  , т.е. считали нашу жидкость несжимаемой (для проводимых ниже аналогий этого достаточно). В пределе
, т.е. считали нашу жидкость несжимаемой (для проводимых ниже аналогий этого достаточно). В пределе 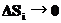 сумма переходит в интеграл, который называется потоком вектора
сумма переходит в интеграл, который называется потоком вектора  через поверхность Sи записывается в виде:
через поверхность Sи записывается в виде: ,
,
 . Это просто обозначение и ничего больше. Понятно, что понятие потока вектора можно ввести и для любого векторного поля, в частности для вектора напряженности электрического поля:
. Это просто обозначение и ничего больше. Понятно, что понятие потока вектора можно ввести и для любого векторного поля, в частности для вектора напряженности электрического поля: ,
,
 ,
,
 ,
,

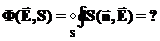 ,
,
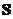 — сфера радиуса
— сфера радиуса  с центром в начале координат.
с центром в начале координат. , полярным углом
, полярным углом 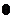 и азимутальным углом
и азимутальным углом 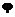 . При этом все точки нашей сферы находятся на расстоянии
. При этом все точки нашей сферы находятся на расстоянии  . Учитывая, что нормаль к площадке равна
. Учитывая, что нормаль к площадке равна  , запишем интересующий нас интеграл в виде:
, запишем интересующий нас интеграл в виде: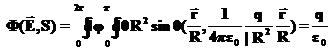 ,
,
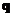 , поток вектора напряженности электрического поля не зависит от положения заряда внутри этой поверхности и равен:
, поток вектора напряженности электрического поля не зависит от положения заряда внутри этой поверхности и равен: ,
,
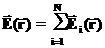 и интеграл равен:
и интеграл равен: ,
,
 , который содержится в внутри поверхности, делённому на электрическую постоянную. Это очень важное уравнение для электростатического поля. Называется это соотношение теоремой Гаусса.
, который содержится в внутри поверхности, делённому на электрическую постоянную. Это очень важное уравнение для электростатического поля. Называется это соотношение теоремой Гаусса.