
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Применение теоремы Гаусса для расчета электрических полей.Вообще говоря, применение теоремы Гаусса для нахождения напряженности электрического поля для системы зарядов является непростой задачей. В ряде случаев проще использовать закон Кулона (9), который для случая непрерывного распределения зарядов по некоторому объему
Однако теорему Гаусса удобно использовать для расчета полей системы зарядов имеющих симметрию. Рассмотрим несколько примеров: 1. Поле бесконечной заряженной плоскости(см. Рис.3). Поверхностная плотность заряда
Рис.3 Из симметрии задачи следует, что вектор напряженности электрического поля направлен перпендикулярно плоскости и зависит только от расстояния до плоскости. Мысленно выделим цилиндрический объем с площадью основания
Отсюда получаем:
Таким образом, поле заряженной плоскости не зависит от расстояния до плоскости и направлено от плоскости, если она заряжена положительно 
Сравнивая с (10) делаем вывод, что с точки зрения размерности с ответом все в порядке. 2. Поле бесконечной заряженной нити (см. Рис.4) с линейной плотностью
Для вычисления напряженности поля построим (мысленно) цилиндр радиуса
что дает:
Правильность размерности легко проверить самостоятельно. 3. Поле заряженного шара. Найдем поле вне заряженного шара. Пусть заряд шара равен
В таком случае модуль напряженности (более точно проекция модуля напряженности на нормаль
и отсюда имеем:
Из этого ответа следует, что заряженная сфера за своими пределами создает такое же поле, как и точечный заряд равный заряду сферы и расположенный в её центре.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 680. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 имеет вид (для случая дискретных зарядов см. (9)):
имеет вид (для случая дискретных зарядов см. (9)):
 (заряд, приходящийся на единицу площади) дана.
(заряд, приходящийся на единицу площади) дана.
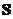 и высотой
и высотой  , основания на расстоянии
, основания на расстоянии  в каждую сторону от поверхности. На рисунке показан цилиндр, направления нормалей к основаниям и боковой поверхности и выбранное нами направление вектора напряженности. В таком случае заряд, который попадает внутрь цилиндра, равен
в каждую сторону от поверхности. На рисунке показан цилиндр, направления нормалей к основаниям и боковой поверхности и выбранное нами направление вектора напряженности. В таком случае заряд, который попадает внутрь цилиндра, равен  , а интеграл по боковой поверхности равен нулю из-за того, что нормаль и вектор напряженности перпендикулярны (
, а интеграл по боковой поверхности равен нулю из-за того, что нормаль и вектор напряженности перпендикулярны (  ). В таком случае остаются только интегралы по двум основаниям на которых вектор напряженности постоянен и направлен вдоль нормали. В этом случае теорема Гаусса записывается в виде:
). В таком случае остаются только интегралы по двум основаниям на которых вектор напряженности постоянен и направлен вдоль нормали. В этом случае теорема Гаусса записывается в виде: ,
,
 ,
,
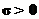 и к плоскости, если она заряжена отрицательно
и к плоскости, если она заряжена отрицательно  . Для дополнительной уверенности в ответе проверим размерность полученного ответа (никогда не помешает), имея ввиду по определению, что
. Для дополнительной уверенности в ответе проверим размерность полученного ответа (никогда не помешает), имея ввиду по определению, что 
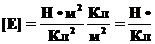 ,
,
 Линейная плотность — это заряд единицы длины нити и, значит размерность
Линейная плотность — это заряд единицы длины нити и, значит размерность 


 и длины
и длины 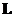 по центру которого проходит наша нить. Заряд, попавший внутрь цилиндра равен
по центру которого проходит наша нить. Заряд, попавший внутрь цилиндра равен  . Из рисунка видно, что вклад в интеграл дает только боковая поверхность. Поэтому, применяя теорему Гаусса, получаем:
. Из рисунка видно, что вклад в интеграл дает только боковая поверхность. Поэтому, применяя теорему Гаусса, получаем: ,
,
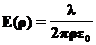 ,
,
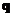 . Поместим заряд в начало координат и мысленно окружим заряд сферой радиуса
. Поместим заряд в начало координат и мысленно окружим заряд сферой радиуса  . Считаем, что радиус сферы больше чем радиус исходного шара. Из симметрии задачи, очевидно, что напряженность поля совпадает с нормалью к сфере. В свою очередь нормаль к сфере направлена по радиус-вектору, проведенному в данную точку сферы:
. Считаем, что радиус сферы больше чем радиус исходного шара. Из симметрии задачи, очевидно, что напряженность поля совпадает с нормалью к сфере. В свою очередь нормаль к сфере направлена по радиус-вектору, проведенному в данную точку сферы: ,
,
 ) находится из следующего уравнения:
) находится из следующего уравнения: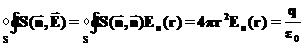 ,
,
