
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Напряженность электрического поля.Стр 1 из 4Следующая ⇒ Электрическое поле в вакууме. Закон Кулона. Принцип суперпозиции. Электрические поля. Напряженность электрического поля. Поток вектора через поверхность. Теорема Гаусса. Применение теоремы Гаусса для расчета электрических полей. Потенциал электрического поля. Эквипотенциальные поверхности.
Закон Кулона. Принцип суперпозиции. Электрические поля. Напряженность электрического поля. Два заряда взаимодействуют друг с другом так, что сила взаимодействия пропорциональна модулю произведения зарядов и обратно пропорциональна квадрату расстояния между зарядами. Конкретная запись величины силы взаимодействия зависит от системы единиц, которая используется. Так в системе (СГСЕ) (сантиметр, грамм, секунда) заряд является производной величиной, и закон Кулона записывается в виде
и это уравнение дает не только величину силы, с которой два заряда взаимодействуют, но и служит для определения размерности заряда
Величина  1. точечность зарядов — то есть расстояние между заряженными телами много больше их размеров.
4. и ещё одно неприятное (особенно для студентов) обстоятельство. В зависимости от системы единиц формулы выглядят по разному (см. (1) и (2)). Поэтому когда будете изучать этот раздел, то пользуйтесь учебником, в котором используется система единиц СИ. Кулон — очень большая величина. Чтобы понять это решим следующую задачу: Задача 1. С какой силой взаимодействуют два заряда по 1 Кл каждый на расстоянии 1 км друг от друга? Решение: В действительности заряд не бывает любым. Одинаковый по модулю и самый маленький заряд имеют протон (положительный заряд) и электрон (отрицательный заряд). Этот заряд называется элементарным и равен:
Заряда меньшего, чем элементарный не бывает. Вернемся к двум однотонным шарам из вольфрама, которые мы рассматривали раньше. Радиус каждого из шаров равен примерно 23 сантиметра. Мы знаем (из школьной химии), что все вещества состоят из атомов, а каждый атом содержит одинаковое число протонов и электронов. Поэтому атомы (да и молекулы) электрически нейтральны. Так вот, возвращаясь к нашим шарам, зададим вопрос о том с какой силой эти шары будут отталкиваться, если каждый из шаров потеряет одну миллиардную (
Жуткой величины сила, которую и представить невозможно. Совсем чуть-чуть нарушилась электронейтральность и такая сила. Можно утешиться только тем, что даже таких слабых нарушений не бывает, поскольку отнять такое количество электронов у вольфрама не дадут те же самые Кулоновские силы. Так, например чтобы отнять последний электрон у поверхности шара нужно его тащить с силой
Из этого выражения видно, что:
Ну а если у нас нужно найти силу, когда на наш заряд действует не один, а много точечных зарядов? В этом случае сила есть векторная сумма сил, которые действуют на данную частицу со стороны каждой из частиц. При этом сила, с которой i – я частица действует на выделенную частицу считается так, как будто других частиц нет. Такая процедура называется принципом суперпозиции. Все, как и было в механике, берутся все силы, которые действуют на данную частицу со стороны остальных и складываются (Силы это вектора и складываются вектора). Таким образом, если у нас имеется частица с зарядом
Получается, что заряженные частицы создают поле, которое и определяет как сильно (и в каком направлении) эти частицы действуют на данный заряд. Это поле можно характеризовать вектором напряженности электрического поля
Физический смысл этого вектора понятен из формулы (8). Из этой формулы видно, что численно напряженность электрического поля равна силе, которая действует на единичный положительный заряд. Из уравнения (8) (или (9)) видно, что размерность напряженности электрического поля равна размерности силы поделённой на величину заряда. Эта величина называется Вольт/метр:
В принципе напряженность поля можно измерить. Для этого берётся известной величины заряд и измеряется сила (направление и величина) действующая на этот заряд в данной точке. И в этом месте надо задуматься, а какой величины нужно взять заряд. Его нужно взять таким, чтобы он занимал мало места в пространстве, иначе мы не сможем сказать, что меряем поле в данной точке. И еще заряд, с помощью которого мы измеряем поле, должен быть маленьким, таким маленьким, чтобы заряды создающие поле не смещались так, чтобы поле заметно изменилось. Иначе мы будем измерять не поле исходных зарядов, а поле зарядов, которые сместились из исходных положений за счет нашего пробного заряда. Таким образом, пробный заряд должен быть:
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 553. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,
 — СГСЕ единица заряда. Мы будем пользоваться системой СИ. В этой системе единицей заряда является Кулон (Кл), а закон кулона имеет вид:
— СГСЕ единица заряда. Мы будем пользоваться системой СИ. В этой системе единицей заряда является Кулон (Кл), а закон кулона имеет вид: .
.
 Здесь (в системе СИ) в качестве основной величины выбирается величина заряда, и называется эта величина Кулон (Кл). На самом деле в качестве основной величины в СИ выбирается сила тока равная одному Амперу (А), которая совсем просто связана с единицей заряда
Здесь (в системе СИ) в качестве основной величины выбирается величина заряда, и называется эта величина Кулон (Кл). На самом деле в качестве основной величины в СИ выбирается сила тока равная одному Амперу (А), которая совсем просто связана с единицей заряда  . А коэффициенты, входящие в уравнение (2) служат для согласования размерностей и равны
. А коэффициенты, входящие в уравнение (2) служат для согласования размерностей и равны .
.
 .
.
 называют электрической постоянной(иногда можно встретить устаревшее названиедиэлектрическая проницаемость вакуума). Важно отметить, что для того, чтобы закон был верен, необходимо выполнение следующих условий:
называют электрической постоянной(иногда можно встретить устаревшее названиедиэлектрическая проницаемость вакуума). Важно отметить, что для того, чтобы закон был верен, необходимо выполнение следующих условий:
 .
.
 ) от всех своих электронов. Одна миллиардная от всех электронов в одной тонне вольфрама равна
) от всех своих электронов. Одна миллиардная от всех электронов в одной тонне вольфрама равна  и, соответственно заряд каждого шара равен
и, соответственно заряд каждого шара равен  . Учитывая, что расстояние между центрами наших шаров равно 46 сантиметрам найдем силу, с которой они отталкиваются:
. Учитывая, что расстояние между центрами наших шаров равно 46 сантиметрам найдем силу, с которой они отталкиваются: .
.
 . Где взять такую силу? Итак, вернемся к закону Кулона. Запись, приведенная в формуле (2) совершенно неприемлема для людей так хорошо знающих математику, как студент второго курса. Мы уже писали правильное выражение, и перепишем еще раз выражение для силы, с которой частица 2действует на частицу1:
. Где взять такую силу? Итак, вернемся к закону Кулона. Запись, приведенная в формуле (2) совершенно неприемлема для людей так хорошо знающих математику, как студент второго курса. Мы уже писали правильное выражение, и перепишем еще раз выражение для силы, с которой частица 2действует на частицу1: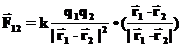
 и радиус вектором
и радиус вектором  и она взаимодействует с N заряженными, неподвижными частицами, то сила, с которой эти частицы действуют на неё согласно принципу суперпозиции равна:
и она взаимодействует с N заряженными, неподвижными частицами, то сила, с которой эти частицы действуют на неё согласно принципу суперпозиции равна:
 , который, согласно (8) равен:
, который, согласно (8) равен:
