
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные физические величины и законы
Закон Кулона где Напряженность где Напряженность и потенциал электрического поля точечного заряда Для точек электрического поля вблизи ( где Для точек электрического поля вблизи ( где Принцип суперпозиции электрических полей где Электроемкость уединенного проводника где Энергия уединенного заряженного проводника Энергия взаимодействия системы точечных зарядов  где Электроемкость конденсатора где Электроемкость плоского конденсатора где Энергия заряженного конденсатора Объемная плотность энергии электрического поля Электроемкость системы конденсаторов при параллельном и последовательном соединении где Сила и плотность постоянного электрического тока где Для изменяющегося тока Сопротивление однородного проводника где Сопротивление проводников при параллельном и последовательном соединении где Электродвижущая сила где Закон Ома: § для однородного участка цепи
Рисунок 6. § для неоднородного участка цепи
Рисунок 7. §
Рисунок 8.
где Работа тока на участке цепи за время Мощность тока Закон Джоуля-Ленца где Правила Кирхгофа где
Дано: Найти: . Рисунок 9. Решение. Напряженность По определению же этой величины имеем Значит где Запишем условие равновесия заряженного шарика Введем силу Очевидно, что силы В скалярном виде Как видно из рисунка Тогда уравнение (1.2) приобретает вид Отсюда Учитывая, что Пример 2.Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобрел скорость 2) поверхностную плотность заряда на пластинах. Дано: Найти: Решение. 1). По определению где Работа где Как видно из условия, Таким образом уравнение (2.1) приобретает вид Подставим численные значения величин 2). Поверхностная плотность Отсюда С другой стороны, напряженность В нашем случае Таким образом, уравнение (2.2) с учетом формулы (2.3) принимает вид Подставим численные значения Пример 3.К воздушному конденсатору, заряженному до разности потенциалов Дано: Найти: Решение. Емкость плоского конденсатора определяется формулой В нашем случае Отсюда следует С другой стороны, из определения емкости конденсатора · для начального состояния первого конденсатора · для конечных состояний первого и второго конденсаторов где Из этих уравнений следует По закону сохранения зарядов имеем То есть Отсюда Подставляя формулу (3.2) в уравнение (3.1), окончательно получаем Пример 4. Э. д. с. батареи Дано: Найти: Решение. Мощность, выделяемую во внешней цепи, определяем по формуле где По закону Ома для замкнутой цепи где Учитывая формулу (4.1), получаем Для нахождения Отсюда получаем Значит, Тогда формула (4.2) примет вид Как видно из формулы (4.1) Отсюда находим Подставляя формулу (4.4) в уравнение (4.3) , окончательно находим С учетом заданных величин получаем
Дано: Найти: Решение. Закон Джоуля—Ленца в виде Здесь сила тока I является некоторой функцией времени. В нашем случае где k — коэффициент пропорциональности, численно равный приращению силы тока в единицу времени, т. е. С учетом (5.2) формула (5.1) примет вид Для определения теплоты, выделившейся за конечный промежуток времени Δt, выражение (5.3) надо проинтегрировать в пределах от t1 до t2: При определении теплоты, выделившейся за первую секунду, пределы интегрирования При определении теплоты Q2 пределы интегрирования Следовательно, т. е. за вторую секунду выделится теплоты в 7 раз больше, чем за первую. Пример 6.Три источника тока с
Дано: Найти:
Рисунок 11. Решение. Воспользуемся правилами Кирхгофа. Выберем направления токов В соответствии с первым правилом В соответствии со вторым правилом для контура для контура
Решая эту систему, находим Для нахождения разности потенциалов применив его для любой из ветвей данной цепи. Выберем, например, первую ветвь цепи Получим Отсюда После подстановки численных значений величин находим
Задачи
3.01. Две параллельные плоскости, заряженные с поверхностными плотностями 3.02. Расстояние d между двумя точечными зарядами
3.03. На бесконечном тонкостенном цилиндре диаметром 3.04. Два одинаковых металлических заряженных шара находятся на расстоянии 3.05. Электрон, обладающий кинетической энергией 3.06. Определить потенциальную энергию системы двух точечных зарядов 3.07. Поле образовано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда 3.08. Пылинка массой 3.09. Три одинаковых капли ртути, заряженных до потенциала 3.10. Точечные заряды 3.11. Между пластинами плоского конденсатора вложена тонкая слюдяная пластинка. Какое давление испытывает эта пластинка при напряженности электрического поля 3.12. Плоский конденсатор с площадью пластин
3.13. Расстояние между пластинами плоского конденсатора 3.14. Емкость плоского конденсатора 3.15. Плоский конденсатор состоит из двух круглых пластин радиусом
3.16. Пластины плоского конденсатора площадью 100 см2 каждая притягиваются друг к другу с силой 3.17. Два конденсатора емкостью 3.18. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектриков: слоем стекла толщиной 3.19. Разность потенциалов между пластинами плоского конденсатора площадью 100 см2 каждая равна 280 В. Поверхностная плотность заряда на пластинах 3.20. Плоский воздушный конденсатор с площадью пластин 100 см2 и расстоянием между ними 1 мм заряжен до 100 В. Затем пластины раздвигаются до расстояния 25 мм. Найти энергию конденсатора до и после раздвижения пластин, если источник напряжения перед раздвижением отключается. 3.21. Имеется 120-вольтовая лампочка мощностью 40 Вт. Какое добавочное сопротивление надо включить последовательно с лампочкой, чтобы она давала нормальный накал при напряжении в сети 220 В? Сколько метров нихромовой проволоки диаметром 0,3 мм надо взять, чтобы получить такое сопротивление? 3.22. В сеть с напряжением 3.23. Определить число электронов, проходящих в секунду через единицу площади поперечного сечения железной проволоки длиной 3.24. Сила тока в проводнике равномерно увеличивается от нуля до некоторого максимального значения в течение времени 3.25. От батареи, э. д. с. которой 3.26. Э. д. с. батареи 3.27. Э. д. с. батареи 3.28. При внешнем сопротивлении 3.29. По проводнику сопротивлением 3.30. Элемент замыкают сначала на внешнее сопротивление 3.31. В схеме рисунок 12
Рисунок 12. 3.32. Определить силу тока в каждом элементе и напряжение на зажимах сопротивления 3.33. Какая разность потенциалов получается на зажимах двух элементов, включенных параллельно, если их э.д.с. равны соответственно 3.34. Определить силы токов на всех участках электрической цепи (см. рисунок 13), если
Рисунок 13. Рисунок 14. 3.35. Три сопротивления
Рисунок 15. Рисунок 16. 3.37. Определить силу тока в сопротивлении R3(рисунок 15) и напряжение на концах этого сопротивления, если 3.38. Два источника тока 3.39. В схеме рисунка 17
Рисунок 17. 3.40. В схеме рисунка 17
ЭЛЕКТРОМАГНЕТИЗМ
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 444. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
, – сила взаимодействия двух точечных зарядов
– сила взаимодействия двух точечных зарядов  и
и  в среде с диэлектрической проницаемостью
в среде с диэлектрической проницаемостью 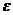 .
.  – электрическая постоянная
– электрическая постоянная  ,
,  – расстояние между зарядами.
– расстояние между зарядами. и потенциал
и потенциал  в точках электрического поля
в точках электрического поля ;
;  ;
;  ,
, – сила, действующая со стороны электрического поля на точечный заряд
– сила, действующая со стороны электрического поля на точечный заряд 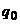 , помещенный в рассматриваемую точку;
, помещенный в рассматриваемую точку;  – потенциальная энергия заряда
– потенциальная энергия заряда  – работа перемещения заряда
– работа перемещения заряда  – работа перемещения заряда
– работа перемещения заряда  в точках на расстоянии
в точках на расстоянии  ;
;  .
. ) заряженной плоскости
) заряженной плоскости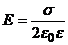 ;
;  ,
, – поверхностная плотность заряда плоскости
– поверхностная плотность заряда плоскости  ;
;  – площадь плоскости;
– площадь плоскости;  – расстояние от плоскости до точек 1 и 2.
– расстояние от плоскости до точек 1 и 2. ) заряженного цилиндра (нити) длины
) заряженного цилиндра (нити) длины 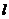
 ;
;  ;
;  ;
;  при
при  ,
, – линейная плотность заряда цилиндра (нити)
– линейная плотность заряда цилиндра (нити)  ;
;  – радиус цилиндра;
– радиус цилиндра;  ;
; 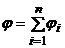 ,
, и потенциалами
и потенциалами  в рассматриваемой точке.
в рассматриваемой точке. ,
, .
. ,
, .
. ;
;  ,
, – напряжение на обкладках конденсатора,
– напряжение на обкладках конденсатора, 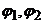 – потенциалы обкладок конденсатора.
– потенциалы обкладок конденсатора. ,
,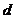 – расстояние между пластинами.
– расстояние между пластинами. .
. .
. ;
;  ,
, – емкость i-го конденсатора,
– емкость i-го конденсатора,  – число конденсаторов.
– число конденсаторов. ;
; 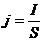 ,
, ,
,  .
. ,
, – удельное сопротивление материала проводника,
– удельное сопротивление материала проводника,  ;
;  ,
,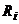 – сопротивление i-го проводника,
– сопротивление i-го проводника,  ,
, – работа сторонних сил, по перемещению заряда
– работа сторонних сил, по перемещению заряда 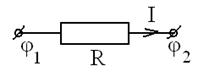
 ;
; 
 ,
,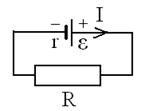 для замкнутой цепи
для замкнутой цепи ,
, и
и  – потенциалы начальной и конечной точек участка цепи,
– потенциалы начальной и конечной точек участка цепи,  .
. .
. ,
, – количество теплоты, выделяющееся на участке цепи с сопротивлением
– количество теплоты, выделяющееся на участке цепи с сопротивлением  .
. ;
;  ,
, – силы токов в каждом из
– силы токов в каждом из  – токи и сопротивления участков цепи произвольного замкнутого контура;
– токи и сопротивления участков цепи произвольного замкнутого контура; 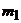 – число участков цепи, на которые этот контур разбивается узлами;
– число участков цепи, на которые этот контур разбивается узлами;  – э.д.с. источников тока, имеющихся в рассматриваемом контуре.;
– э.д.с. источников тока, имеющихся в рассматриваемом контуре.;  – число источников тока в контуре.
– число источников тока в контуре.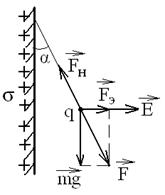 Пример 1.К бесконечной, равномерно заряженной, вертикальной плоскости подвешен на нити одноименно заряженный шарик массой
Пример 1.К бесконечной, равномерно заряженной, вертикальной плоскости подвешен на нити одноименно заряженный шарик массой  и зарядом
и зарядом  , Натяжение нити, на которой висит шарик,
, Натяжение нити, на которой висит шарик,  . Найти поверхностную плотность заряда на плоскости.
. Найти поверхностную плотность заряда на плоскости.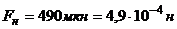 ;
; ;
; .
. .
. или
или 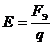 .
. , (1.1)
, (1.1) – сила, действующая на заряд
– сила, действующая на заряд  .
. .
. и
и  .
. . (1.2)
. (1.2) .
. .
. . (1.3)
. (1.3) ,
,  (воздух) и
(воздух) и  , вычисляем
, вычисляем  .
. . Расстояние между пластинами
. Расстояние между пластинами  . Найти: 1) разность потенциалов между пластинами;
. Найти: 1) разность потенциалов между пластинами; ;
;  .
. ,
,  , (2.1)
, (2.1) – численное значение заряда электрона.
– численное значение заряда электрона. ,
, – масса электрона ,
– масса электрона ,  и
и  – начальная и конечная скорости электрона.
– начальная и конечная скорости электрона. и получаем
и получаем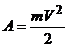 .
. .
. .
. .
. . (2.2)
. (2.2) однородного поля связана с разностью потенциалов
однородного поля связана с разностью потенциалов 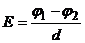 . (2.3)
. (2.3) .
. .
. и отключенному от источника напряжения, присоединен параллельно второй конденсатор таких же размеров и формы, но с другим диэлектриком (стекло). Определить диэлектрическую проницаемость εстекла, если после присоединения второго конденсатора разность потенциалов уменьшилась до
и отключенному от источника напряжения, присоединен параллельно второй конденсатор таких же размеров и формы, но с другим диэлектриком (стекло). Определить диэлектрическую проницаемость εстекла, если после присоединения второго конденсатора разность потенциалов уменьшилась до  .
. ;
;  .
. .
. ;
;  .
. . (3.1)
. (3.1)
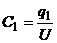 ;
;  ,
, – заряды конденсаторов после их параллельного соединения.
– заряды конденсаторов после их параллельного соединения. ;
;  ;
;  .
. , так как конденсаторы отключены от источника напряжения.
, так как конденсаторы отключены от источника напряжения. .
. . (3.2)
. (3.2) ;
;  .
. . Наибольшая сила тока, которую может дать батарея,
. Наибольшая сила тока, которую может дать батарея,  . Определить максимальную мощность
. Определить максимальную мощность  , которая может выделяться во внешней цепи.
, которая может выделяться во внешней цепи. .
. ,
, . (4.2)
. (4.2) вычислим производную
вычислим производную  и приравняем ее нулю
и приравняем ее нулю ;
;  .
.
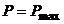 , если внешнее сопротивление цепи равно внутреннему.
, если внешнее сопротивление цепи равно внутреннему. . (4.3)
. (4.3) при равенстве нулю внешнего сопротивления (ток короткого замыкания)
при равенстве нулю внешнего сопротивления (ток короткого замыкания) .
. . (4.4)
. (4.4) .
. .
. Пример 5. Сила тока в проводнике сопротивлением
Пример 5. Сила тока в проводнике сопротивлением  нарастает в течение времени
нарастает в течение времени  по линейному закону от
по линейному закону от  до
до  (рисунок 10). Определить теплоту Q1, выделившуюся в этом проводнике за первую и Q2 —за вторую секунды, а также найти отношение
(рисунок 10). Определить теплоту Q1, выделившуюся в этом проводнике за первую и Q2 —за вторую секунды, а также найти отношение  .
. . Рисунок 10.
. Рисунок 10. . Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде
. Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде . (5.1)
. (5.1) , (5.2)
, (5.2) .
. . (5.3)
. (5.3) .
.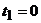 ,
,  и, следовательно,
и, следовательно, .
. ,
,  и
и .
. ,
, ;
;  ;
;  и внутренними сопротивлениями, соответственно,
и внутренними сопротивлениями, соответственно,  ;
; 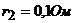 ;
;  , а также сопротивления
, а также сопротивления  ;
;  ;
;  соединены как показано на рисунке 11.
соединены как показано на рисунке 11. Найти токи в каждой ветви цепи и разность потенциалов между точками В и А.
Найти токи в каждой ветви цепи и разность потенциалов между точками В и А. .
. и укажем на схеме.
и укажем на схеме. . (6.1)
. (6.1)
 (обход по часовой стрелке)
(обход по часовой стрелке) ; (6.2)
; (6.2) (обход против часовой стрелки)
(обход против часовой стрелки) . (6.3)
. (6.3) Уравнения (6.1), (6.2) и (6.3) после подстановки заданных численных значений величин образуют систему трех уравнений для отыскания токов
Уравнения (6.1), (6.2) и (6.3) после подстановки заданных численных значений величин образуют систему трех уравнений для отыскания токов  .
. ;
;  ;
; 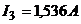 .
. воспользуемся законом Ома для неоднородного участка цепи
воспользуемся законом Ома для неоднородного участка цепи .
. .
. .
.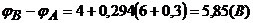 .
. и
и  , находятся на расстоянии
, находятся на расстоянии  друг от друга. Определить разность потенциалов между плоскостями.
друг от друга. Определить разность потенциалов между плоскостями. и
и равно 60 см. Определить точку, в которую нужно поместить третий заряд
равно 60 см. Определить точку, в которую нужно поместить третий заряд  так, чтобы система зарядов находилась в равновесии. Определить величину и знак заряда. Устойчивое или неустойчивое будет равновесие?
так, чтобы система зарядов находилась в равновесии. Определить величину и знак заряда. Устойчивое или неустойчивое будет равновесие? равномерно распределен заряд с поверхностной плотностью
равномерно распределен заряд с поверхностной плотностью  . Определить напряженность поля в точке, отстоящей от поверхности цилиндра на
. Определить напряженность поля в точке, отстоящей от поверхности цилиндра на  .
. . Сила отталкивания шаров
. Сила отталкивания шаров 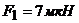 . После того как шары привели в соприкосновение и удалили друг от друга на прежнее расстояние, сила отталкивания возросла и стала равной
. После того как шары привели в соприкосновение и удалили друг от друга на прежнее расстояние, сила отталкивания возросла и стала равной  . Вычислить заряды
. Вычислить заряды  , влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов
, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов  ?
? и
и  , находящихся на расстоянии
, находящихся на расстоянии  друг от друга.
друг от друга. . Определить разность потенциалов U двух точек поля, отстоящих от плоскости на
. Определить разность потенциалов U двух точек поля, отстоящих от плоскости на  и
и  .
. , несущая на себе заряд
, несущая на себе заряд  , влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов
, влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов  пылинка имела скорость
пылинка имела скорость  . Определить скорость пылинки до того, как она влетела в поле.
. Определить скорость пылинки до того, как она влетела в поле.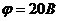 , сливаются в одну. Каков потенциал образовавшейся капли?
, сливаются в одну. Каков потенциал образовавшейся капли? и
и  находятся на расстоянии
находятся на расстоянии  от первого и,
от первого и,  от второго заряда. Определить также силу, действующую в этой точке на точечный заряд
от второго заряда. Определить также силу, действующую в этой точке на точечный заряд  .
. ?
?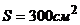 каждая заряжен до разности потенциалов
каждая заряжен до разности потенциалов  . Расстояние между пластинами
. Расстояние между пластинами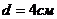 . Диэлектрик – стекло. Определить энергию W поля конденсатора и плотность ω энергии поля.
. Диэлектрик – стекло. Определить энергию W поля конденсатора и плотность ω энергии поля. , разность потенциалов
, разность потенциалов  . Заряд каждой пластины
. Заряд каждой пластины  . Диэлектрик – фарфор. Конденсатор зарядили до разности потенциалов
. Диэлектрик – фарфор. Конденсатор зарядили до разности потенциалов  и отключили от источника напряжения. Какую работу нужно совершить, чтобы вынуть диэлектрик из конденсатора?
и отключили от источника напряжения. Какую работу нужно совершить, чтобы вынуть диэлектрик из конденсатора? каждая. Расстояние между пластинами
каждая. Расстояние между пластинами  . Конденсатор присоединен к источнику напряжения
. Конденсатор присоединен к источнику напряжения  . Определить заряд и напряженность поля конденсатора, если диэлектриком будут: а) воздух; б) стекло.
. Определить заряд и напряженность поля конденсатора, если диэлектриком будут: а) воздух; б) стекло. Пространство между пластинами заполнено слюдой. Найти: 1). заряды, находящиеся на пластинах, 2). напряженность поля между пластинами, 3). энергию в единице объема поля.
Пространство между пластинами заполнено слюдой. Найти: 1). заряды, находящиеся на пластинах, 2). напряженность поля между пластинами, 3). энергию в единице объема поля. и
и  соединены последовательно и присоединены к батарее э. д. с.
соединены последовательно и присоединены к батарее э. д. с.  . Определить заряд каждого конденсатора и разность потенциалов между его обкладками.
. Определить заряд каждого конденсатора и разность потенциалов между его обкладками. и слоем парафина толщиной
и слоем парафина толщиной  . Разность потенциалов между обкладками
. Разность потенциалов между обкладками  . Найти: 1). напряженность поля внутри конденсатора, 2). расстояние между пластинами, 3). скорость, которую получит электрон, пройдя в конденсаторе путь от одной пластины до другой, 4). энергию конденсатора.
. Найти: 1). напряженность поля внутри конденсатора, 2). расстояние между пластинами, 3). скорость, которую получит электрон, пройдя в конденсаторе путь от одной пластины до другой, 4). энергию конденсатора. включили катушку с сопротивлением
включили катушку с сопротивлением 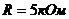 и вольтметр, соединенные последовательно. Показание вольтметра
и вольтметр, соединенные последовательно. Показание вольтметра  . Когда катушку заменили другой, вольтметр показал
. Когда катушку заменили другой, вольтметр показал  . Определить сопротивление другой катушки.
. Определить сопротивление другой катушки.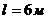 при напряжении на ее концах
при напряжении на ее концах  .
. . За это время в проводнике выделилась теплота
. За это время в проводнике выделилась теплота  . Определить скорость нарастания тока в проводнике, если сопротивление его
. Определить скорость нарастания тока в проводнике, если сопротивление его  .
. , требуется передать энергию на расстояние
, требуется передать энергию на расстояние  . Потребляемая мощность
. Потребляемая мощность  : Найти минимальные потери мощности в сети, если диаметр медных подводящих проводов
: Найти минимальные потери мощности в сети, если диаметр медных подводящих проводов  .
. , внутреннее сопротивление
, внутреннее сопротивление  . Внешняя цепь потребляет мощность
. Внешняя цепь потребляет мощность  . Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь, и ее сопротивление
. Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь, и ее сопротивление  . При силе тока
. При силе тока  к. п. д. батареи
к. п. д. батареи  . Определить внутреннее сопротивление
. Определить внутреннее сопротивление  сила тока в цепи
сила тока в цепи  , при сопротивлении
, при сопротивлении  сила тока
сила тока  . Определить силу тока короткого замыкания источника э. д. с.
. Определить силу тока короткого замыкания источника э. д. с. в проводнике выделилась теплота
в проводнике выделилась теплота  . Определить заряд q, протекший за это время по проводнику. В момент времени, принятый за начальный, ток в проводнике был равен нулю.
. Определить заряд q, протекший за это время по проводнику. В момент времени, принятый за начальный, ток в проводнике был равен нулю. , а затем на внешнее сопротивление
, а затем на внешнее сопротивление  . Найти э.д.с. элемента и его внутреннее сопротивление, если известно, что в каждом из этих случаев мощность, выделяемая во внешней цепи, одинакова и равна 2,54 Вт.
. Найти э.д.с. элемента и его внутреннее сопротивление, если известно, что в каждом из этих случаев мощность, выделяемая во внешней цепи, одинакова и равна 2,54 Вт. и
и  и
и  . Чему равно внешнее сопротивление
. Чему равно внешнее сопротивление  , текущего через
, текущего через  , идущего через
, идущего через  , идущего через сопротивление
, идущего через сопротивление 
 ,
,  ,
,  и
и  .
. и
и 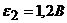 и внутренние сопротивления
и внутренние сопротивления  и
и  ?
? ,
,  ,
,  ,
,  ,
,  ,
,  . Внутренними сопротивлениями источников тока пренебречь.
. Внутренними сопротивлениями источников тока пренебречь.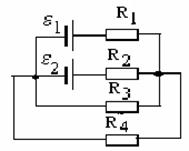

 ,
, 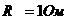 и
и  , а также источник тока
, а также источник тока  3.36. Определить разность потенциалов между точками А и В (рисунок 15), если
3.36. Определить разность потенциалов между точками А и В (рисунок 15), если  ,
, 
 ,
,  ,
,  с внутренним сопротивлением
с внутренним сопротивлением  и
и  с внутренним сопротивлением
с внутренним сопротивлением  , а также реостат
, а также реостат  соединены, как показано на рисунке 16. Определить силы тока в реостате и в источниках тока.
соединены, как показано на рисунке 16. Определить силы тока в реостате и в источниках тока. ,
,  и падение потенциала на сопротивление
и падение потенциала на сопротивление  (ток через
(ток через  направлен сверху вниз) равно 1 В. Найти показание амперметра. Внутренним сопротивлением элементов и амперметра пренебречь.
направлен сверху вниз) равно 1 В. Найти показание амперметра. Внутренним сопротивлением элементов и амперметра пренебречь.
 ,
,  ,
,  ,
,  . Через амперметр идет ток 1 А, направленный от
. Через амперметр идет ток 1 А, направленный от  к
к  . Найти сопротивление
. Найти сопротивление