Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Средняя квадратическая погрешность измерений. Предельная погрешность.
Для оценки степени точности ряда измерений одной и той же величины недостаточно знать арифметическое среднее погрешностей измерений, т.к. в ряде измерений может быть не отражено наличие сравнительно крупных погрешностей разных знаков, поскольку последние взаимно компенсируются. И Гаусс предложил критерий оценки точности измерений, не зависящий от знаков отдельных сравнительно крупных погрешностей ряда – среднюю квадратическую погрешность. Средняя квадратическая ошибка (погрешность) измерений – это корень квадратный из арифметического среднего квадратов истинных погрешностей и вычисляется по формуле:
Поскольку истинное значение измеряемой величины Х не известно, то среднюю квадратическую погрешность m вычисляют по уклонениям
Через уклонения арифметического среднего среднюю квадратическую погрешность определяют по формуле Бесселя: m = Анализ кривой нормального распределения Гаусса показывает, что при достаточно большом числе измерений одной и той же величины случайная погрешность измерения может быть: Больше средней квадратической m в 32 случаях из 100; Больше удвоенной средней квадратической 2m в 5 случаях из 100; Больше утроенной средней квадратической 3m в 3 случаях из 1000. Маловероятно, чтобы случайная погрешность измерения оказалась больше утроенной средней квадратической, поэтому утроенную среднюю квадратическую погрешность считают предельной:
В качестве предельной часто принимают среднюю квадратическую погрешность, равную: 
Средняя квадратическая погрешность суммы измеренных величин Рассмотрим функцию, представляющую собой алгебраическую сумму двух величин:
Z = x ± y, Где x и y – независимые слагаемые. Случайные погрешности слагаемых и их суммы при однократном измерении обозначим соответственно ∆x, ∆y, ∆z, тогда
z+ ∆z = (x+∆x) ± (y +∆y), откуда ∆z = ∆x + ∆y.
Если каждое слагаемое было измерено n раз, то, написав n соотношений (см выше) и возведя каждое в квадрат, получим n выражений:
Сложив левые и правые части n таких уравнений и разделив затем обе части равенства на n, получим:
где [∆Х∆Y] есть сумма произведений случайных погрешностей, которая согласно четвертому свойству случайных погрешностей стремиться к нулю при значительном числе измерений. Тогда, отбросив последнее слагаемое равенства, получим:
В соответствии с формулой можно написать: Где mz, mх, my – средние квадратические погрешности функции и аргументов. По аналогии для алгебраической суммы n независимых величин
Z= Х1±Х2±… ± Хn, Можно записать
т.е. квадрат средней квадратической погрешности алгебраической суммы аргумента равен сумме квадратов средних квадратических погрешностей слагаемых. В частном случае, когда m1=m2=...= mn =m, формула примет вид: mz = m т.е. средняя квадратическая погрешность алгебраической суммы равноточных измерений в
Например, если измерено 9 углов 30-секундным теодолитом, то средняя квадратическая погрешность угловых измерений составит
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 878. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
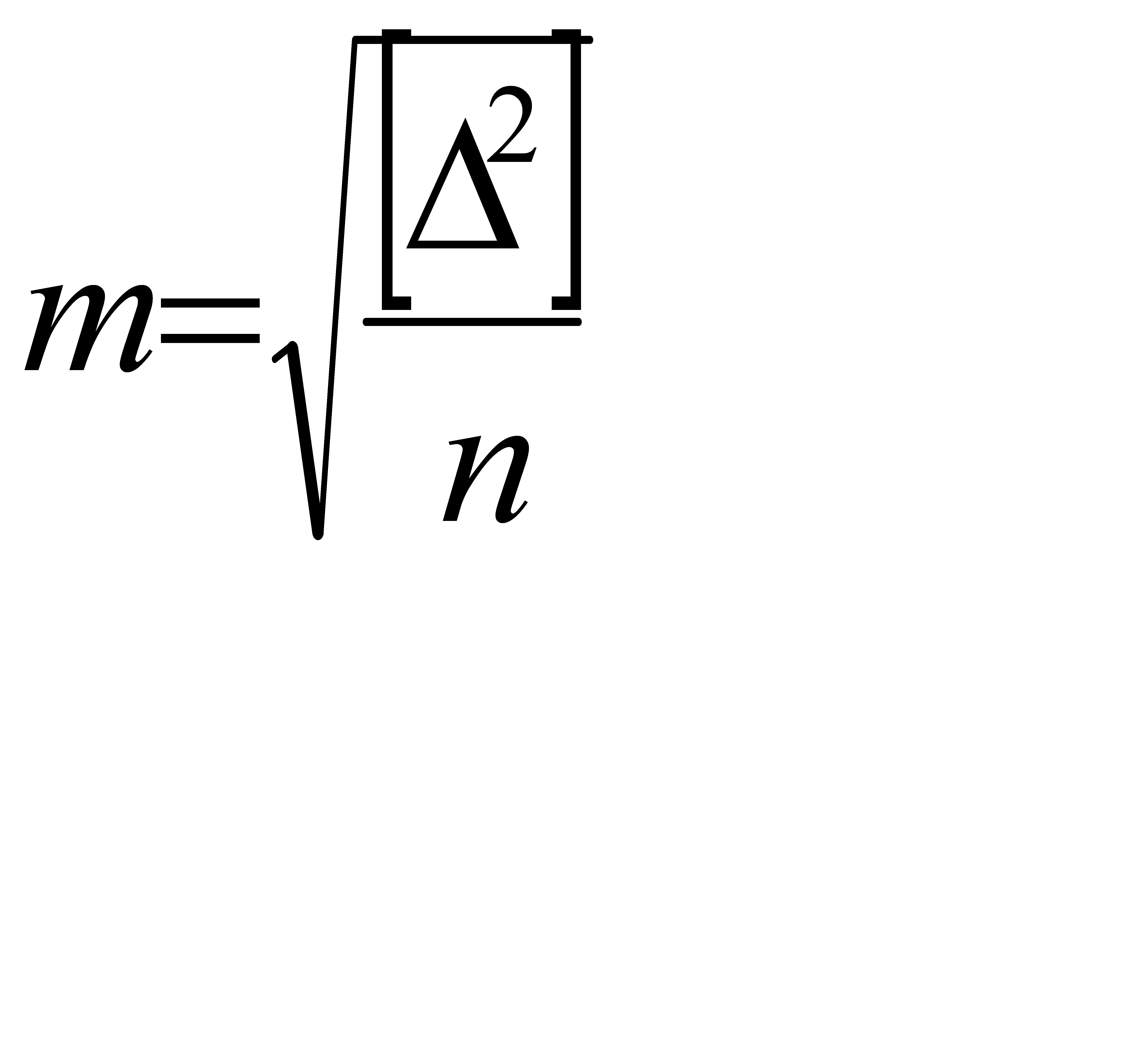 .
.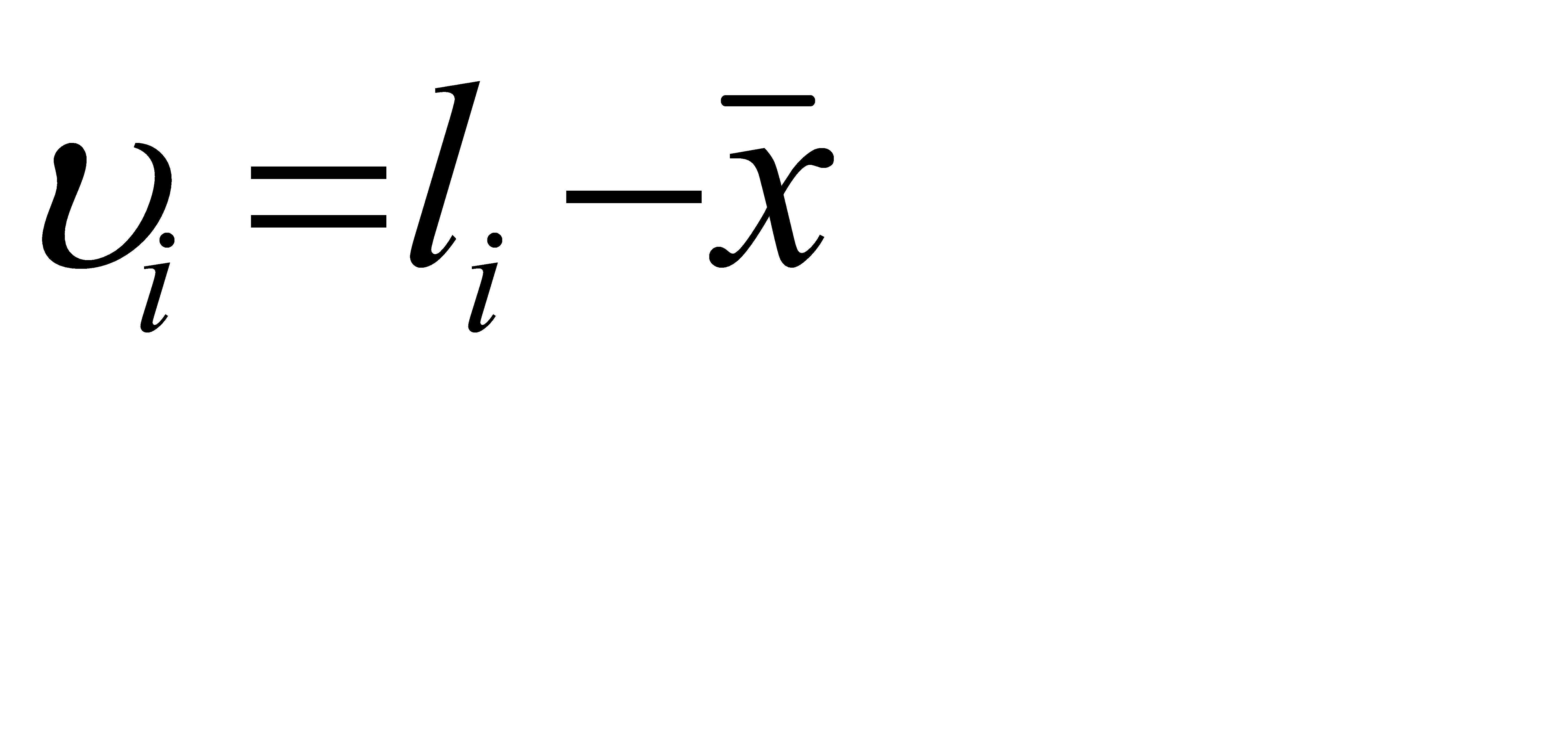
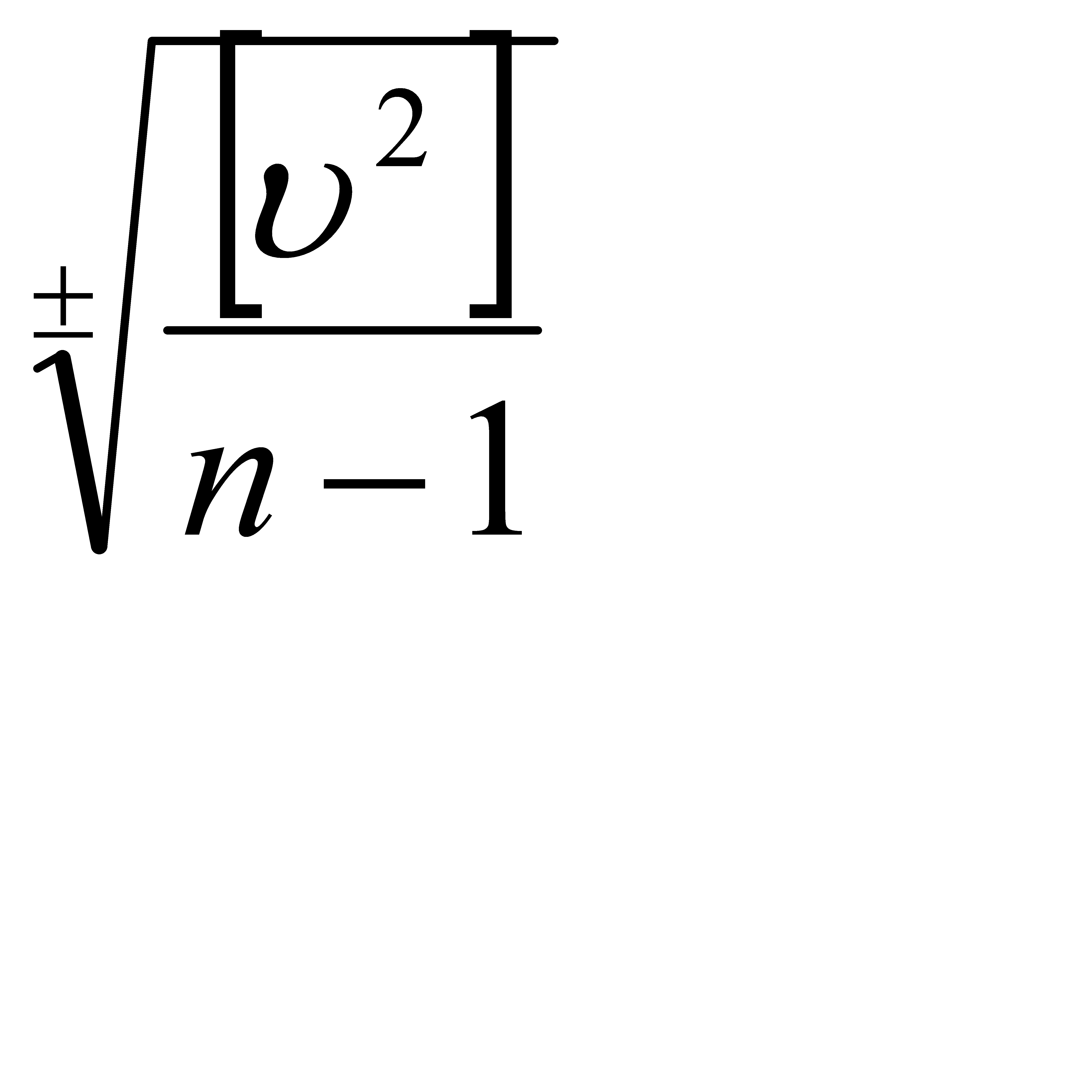 , где [
, где [ 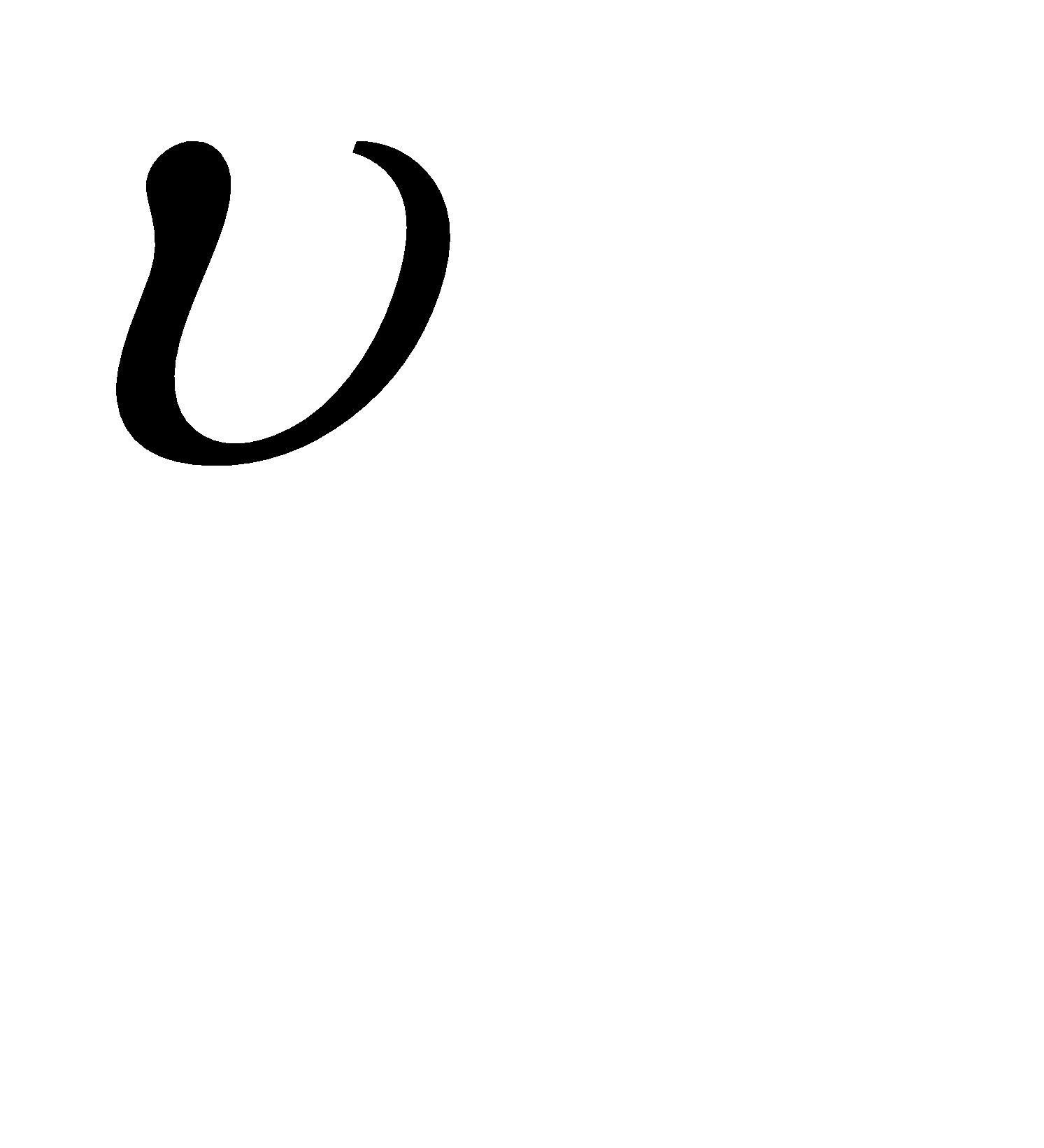 2] – сумма квадратов вероятнейших ошибок; n – число измерений, n-1 – число избыточных измерений.
2] – сумма квадратов вероятнейших ошибок; n – число измерений, n-1 – число избыточных измерений.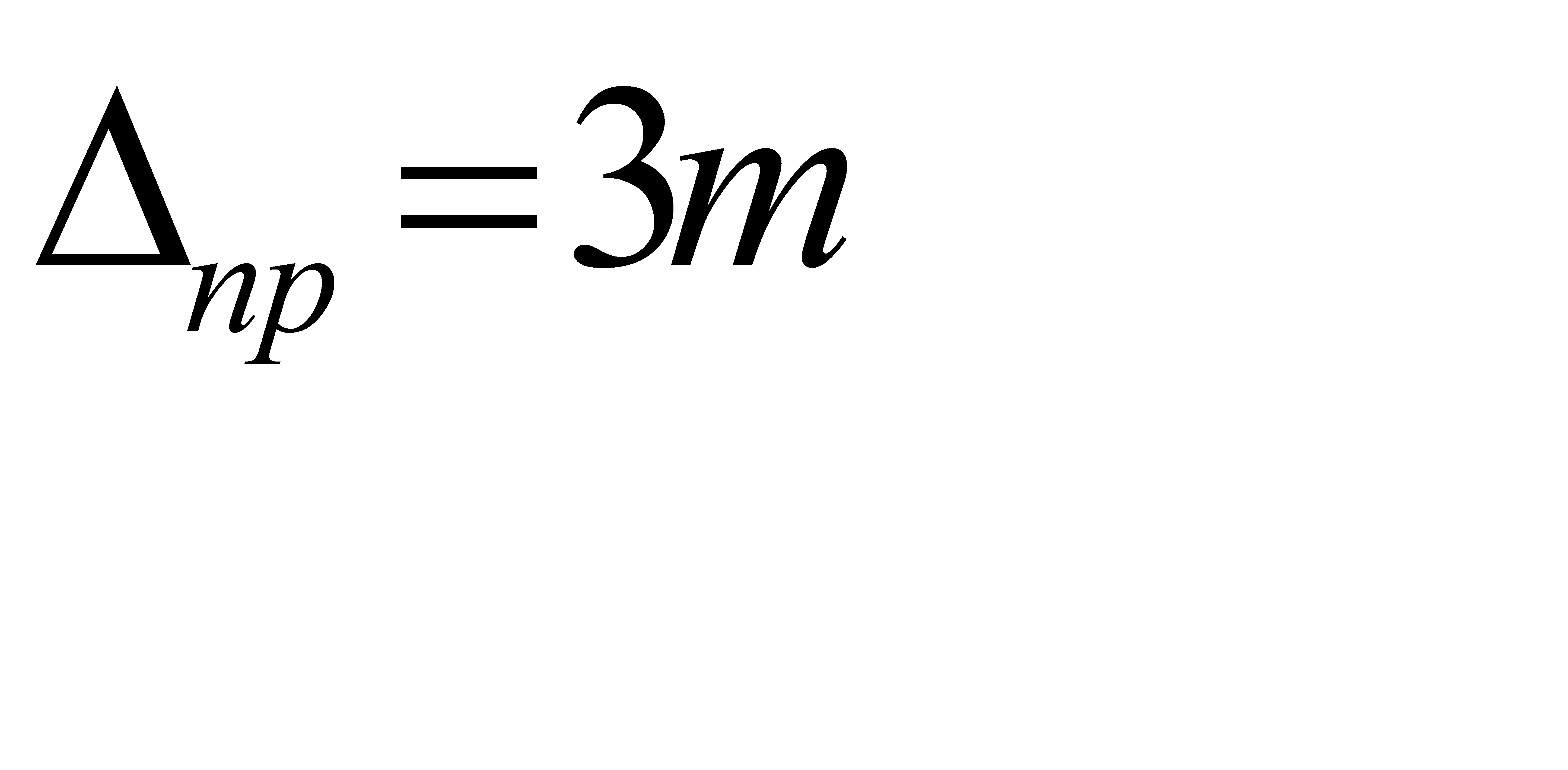
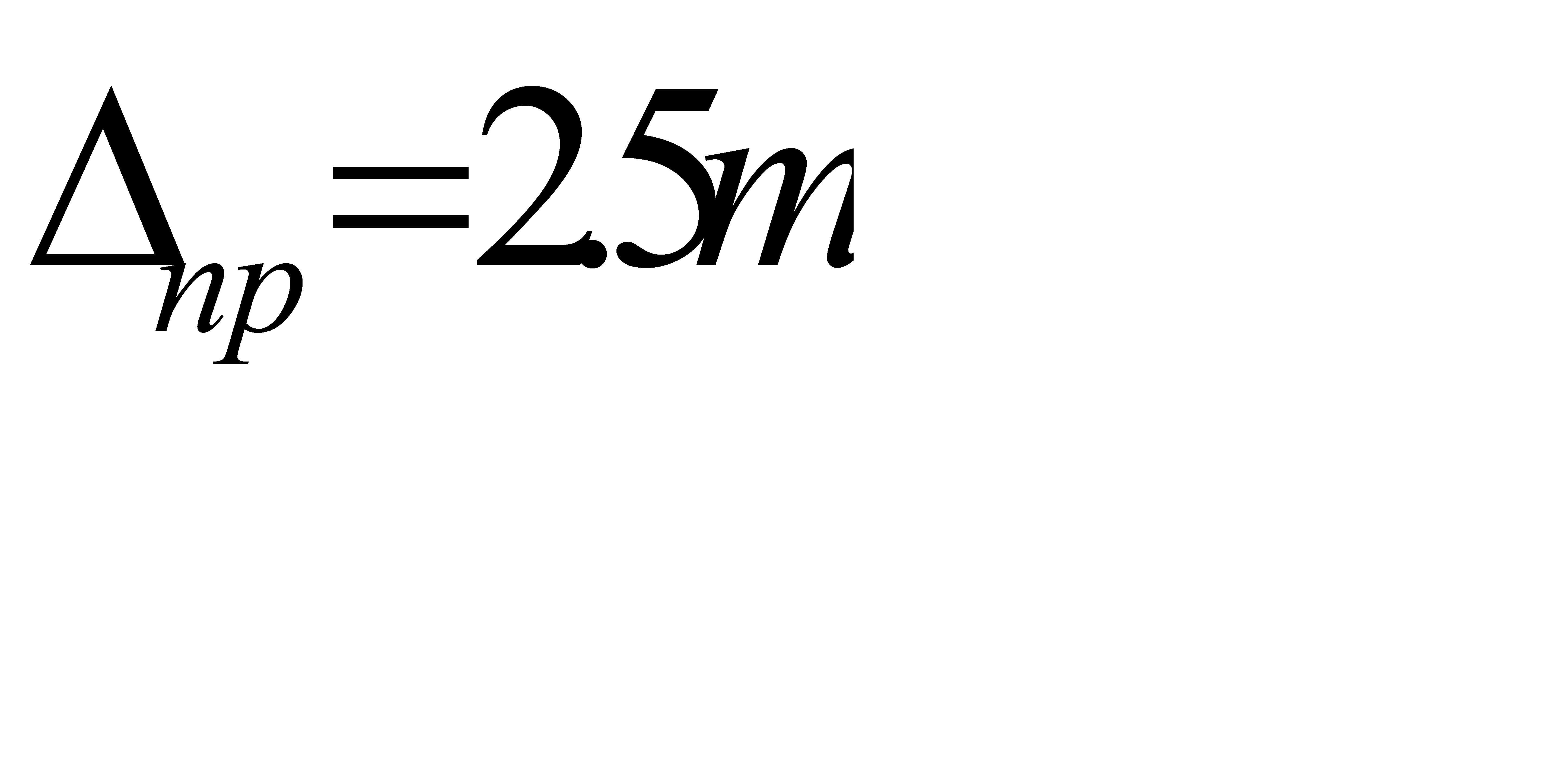 с вероятностью ошибки равной порядка 1%.
с вероятностью ошибки равной порядка 1%.

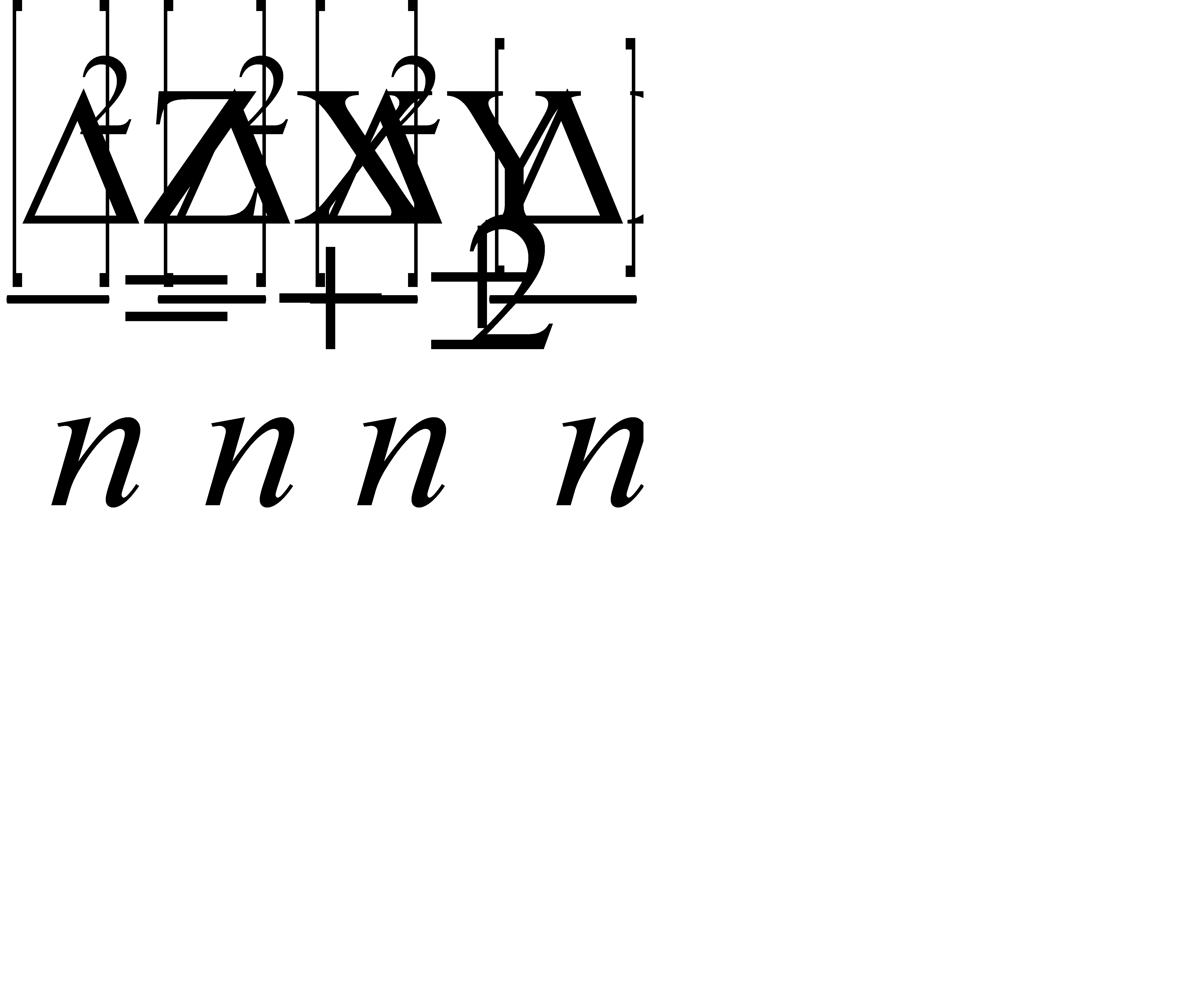
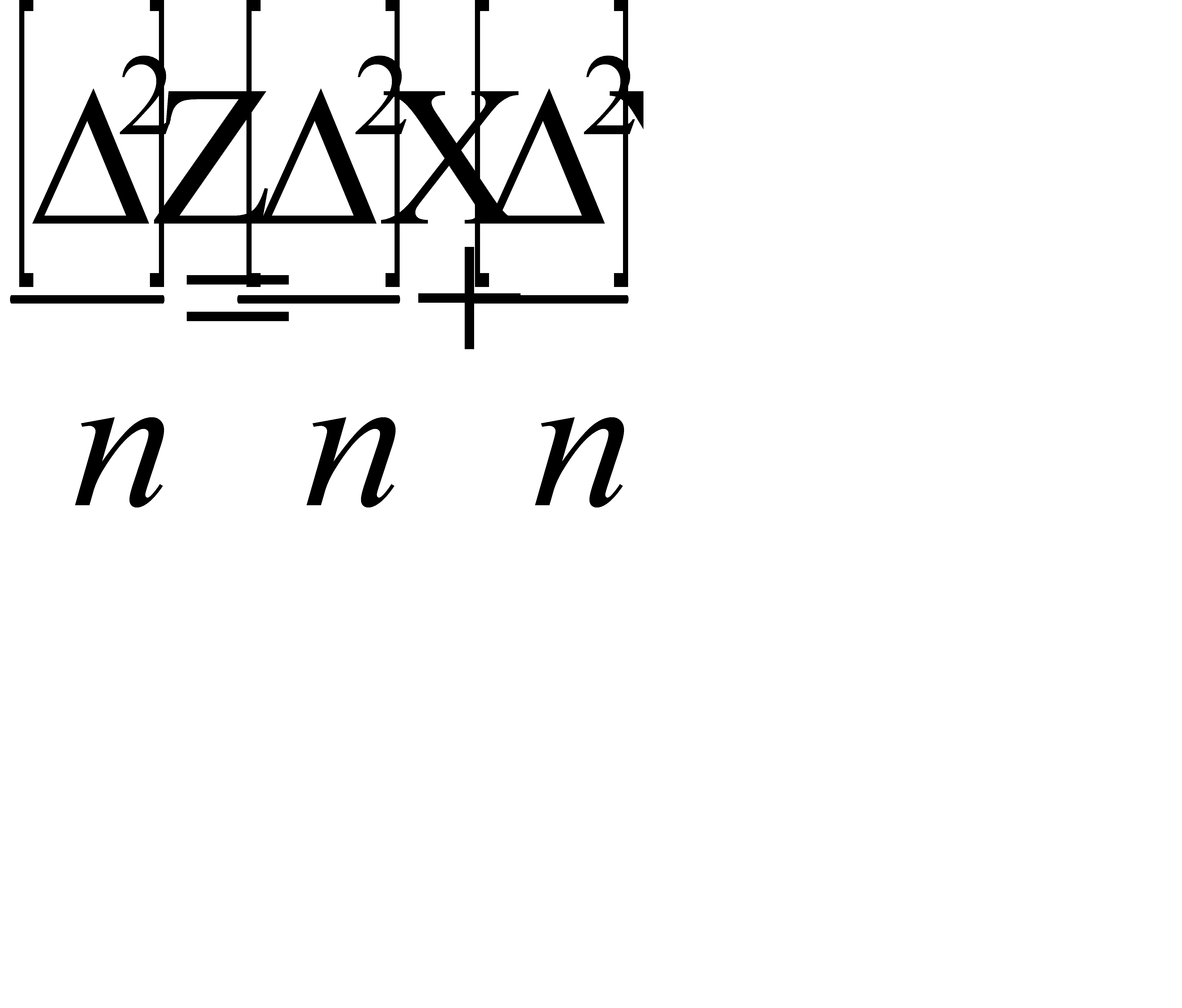
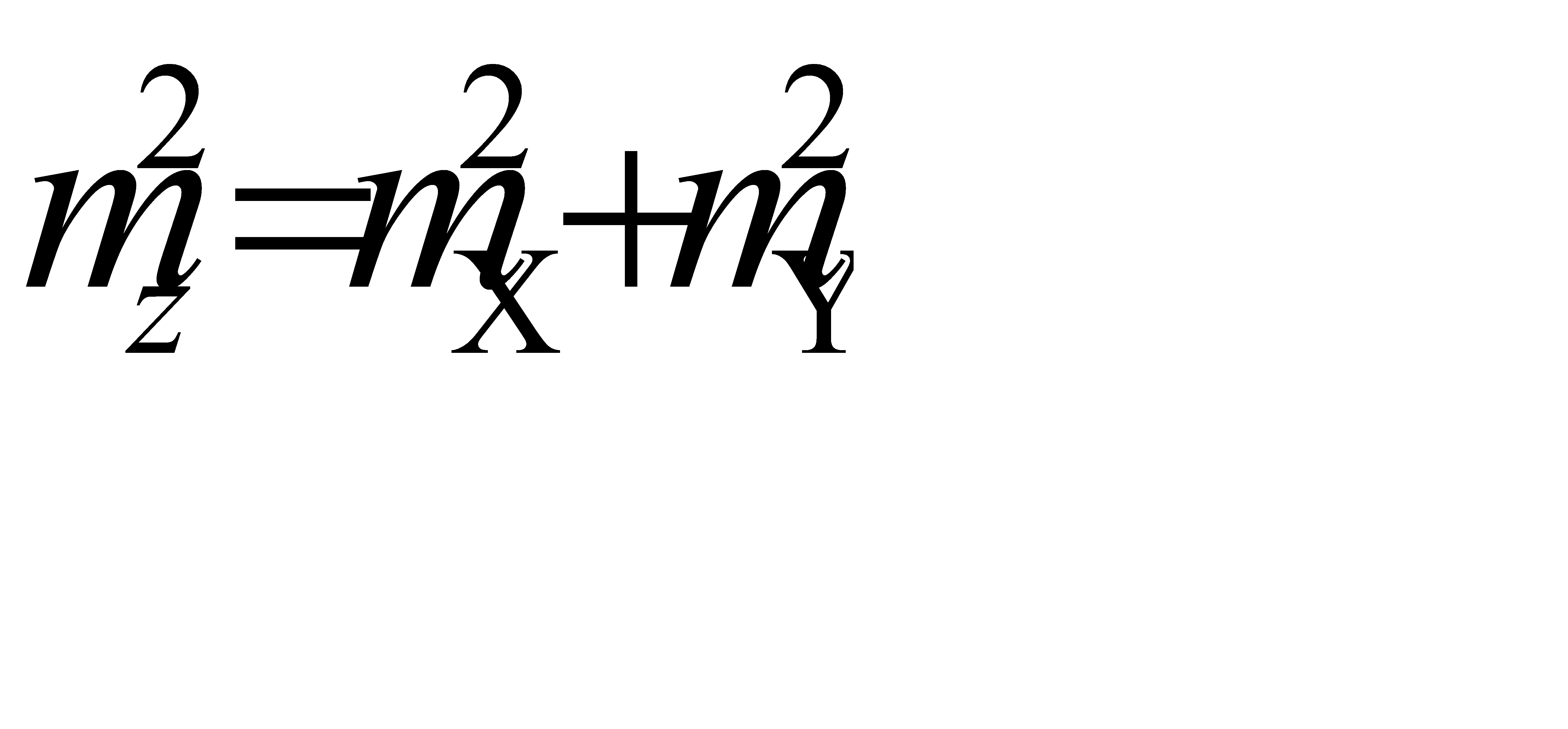 ,
,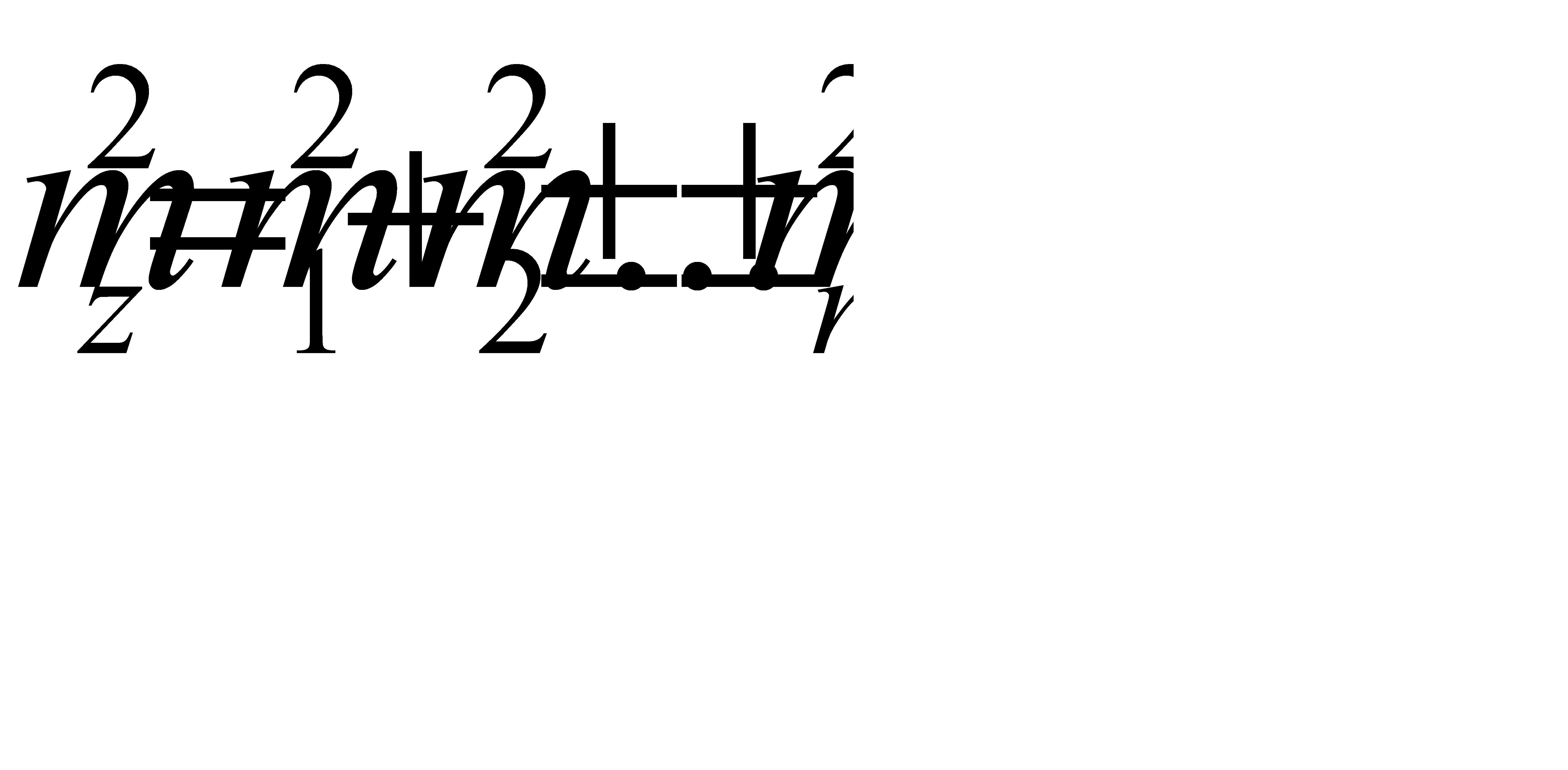 ,
,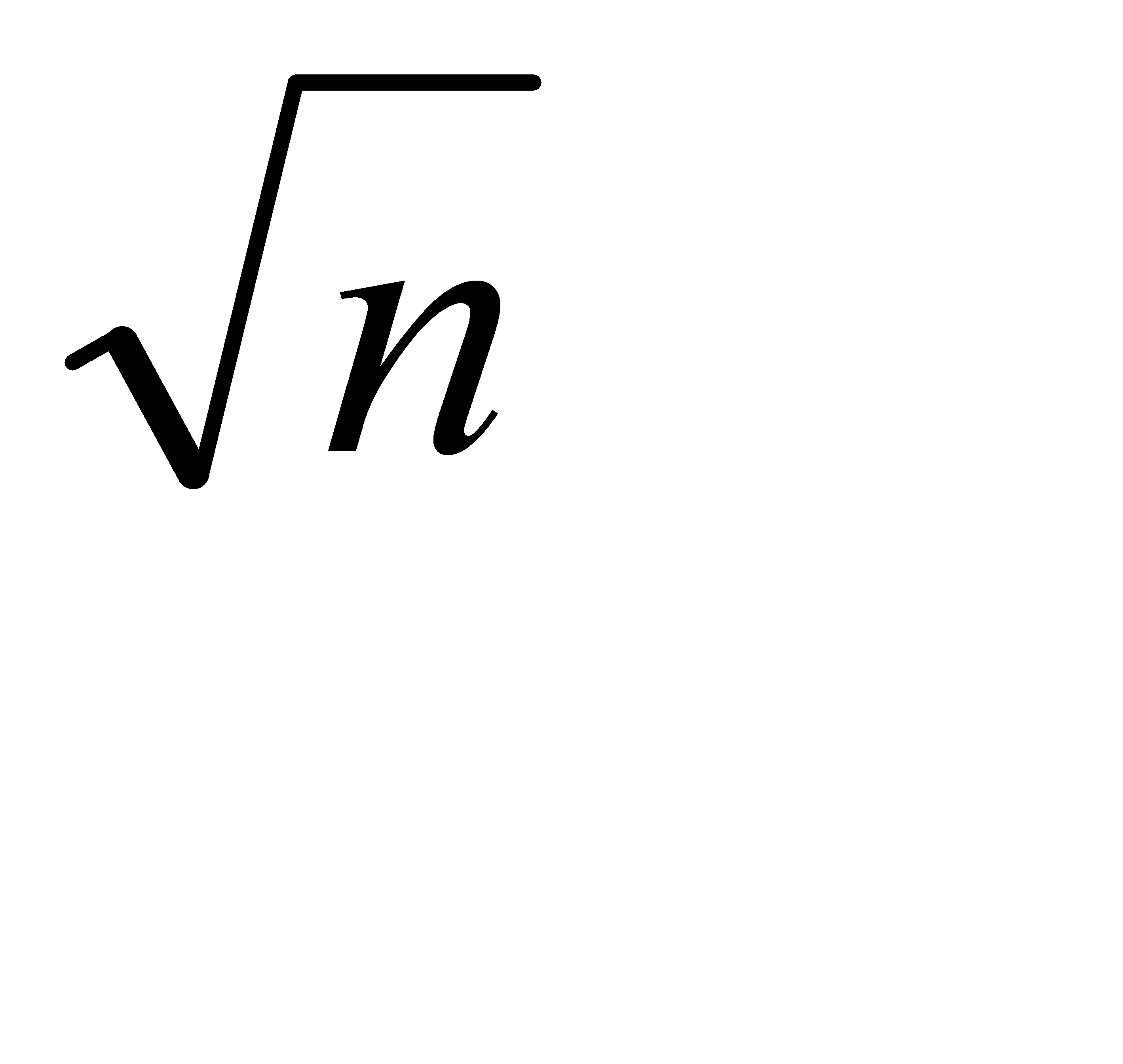 ,
,