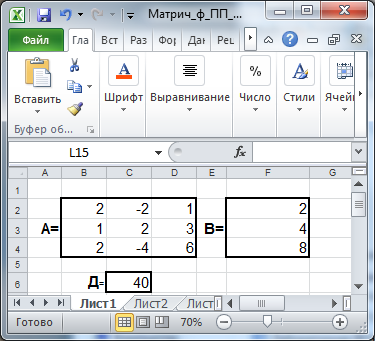
Решение систем линейных уравнений методом наименьших квадратов

Для случаев, когда количество переменных больше, чем количество уравнений (n>m), и если система имеет хотя бы одно решение, то она имеет бесконечное множество решений.

Для случаев, когда количество переменных меньше, чем количество уравнений (n<m), удобно применить более общий подход – метод наименьших квадратов. В этом случае обе части уравнения нужно умножить на транспонированную матрицу системы А^т: А^TАХ=А^TВ.

Затем обе части уравнения нужно умножить на (А^TА)^-1. Если эта матрица существует, то система определена. С учетом того, что (А^TА)^-1(А^TА)= Е, решение системы будет иметь вид:

Х =(А^TА)^-1А^TB.

Пример 4.3.

Используя операции с матрицами, решите систему уравнений:

2х₁ – 2х₂ + х₃ = 2

х₁ + 2х₂ + 3х₃ = 4

2х₁ – 4х₂ + 6х₃ = 8

Решение. Для решения задачи на листе Excel введем матрицу А и вектор В. В некоторой пустой ячейке (С6) найдем определитель матрицы А, используя встроенную функцию МОПРЕД. Если определитель матрицы отличен от 0, то система имеет решение. В нашем случае определитель равен 40, т.е. система решение имеет. Найдем его.

Рис. 22. Исходные данные задачи и определитель матрицы

Выделим на листе диапазон пустых ячеек размерности 3х3, например, В8:D10, вызовем встроенную функцию МОБР, где в качестве массива укажем диапазон ячеек В2:D4, нажмем сочетание клавиш Shift+Ctrl+Enter.

В выделенном диапазоне отобразится обратная матрица. Если Вы не увидели в диапазоне желаемого результата (значение появилось только в одной ячейке, вообще нигде не появилось и др.), нажмите клавишу F2 (в первой ячейке диапазона отобразится =МОБР(B2:D4)), затем Shift+Ctrl+Enter.

Если результат опять Вас не устраивает, значит, Вы не выделили диапазон, равный по размерности обратной матрице!

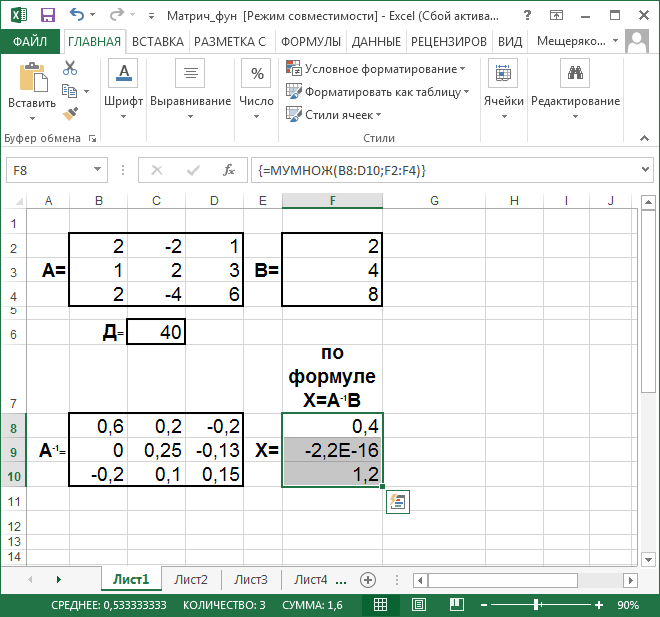
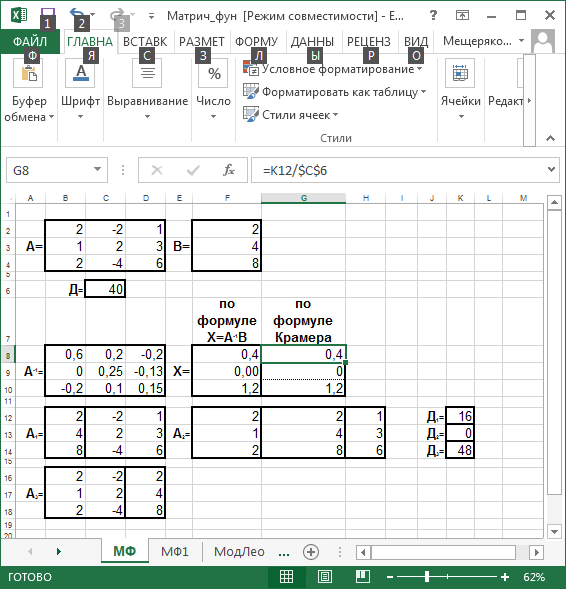
Рис. 23. Решение системы линейных уравнений

Для нахождения вектора Х выделим пустой диапазон ячеек размерности 1х3, например, F8:F10, вызовем встроенную функцию МУМНОЖ, где в качестве массива1 укажем диапазон ячеек с обратной матрицей В8:D10, в качестве массива2 – диапазон ячеек F2:F4 с вектором В и нажмем сочетание клавиш Shift+Ctrl+Enter. Результат выполнения задания приведен на рисунке 23. В ячейке F9 отображается число 0 в экспоненциальном формате, указывающем на некоторую погрешность вычислений.

Пример 4.4.

Решите систему уравнений методом Крамера

2х₁ – 2х₂ + х₃ = 2

х₁ + 2х₂ + 3х₃ = 4

2х₁ – 4х₂ + 6х₃ = 8

Решение. Решим ту же систему методом Крамера и сравним полученные решения. Для этого на листе Excelскопируем и вставим в свободные диапазоны три раза матрицу А (рис. 24).Последовательно заменим столбцы этих матриц на вектор свободных членов: в первой матрице – первый столбец, во второй матрице – второй столбец, в третьей – третий. В ячейках К12:К14 найдем определителиполученных матриц, используя встроенную функцию МОПРЕД. Далее в ячейках G8:G10найдем отношения частных определителей к общему (рис. 24). Полученные разными способами решения совпадают.

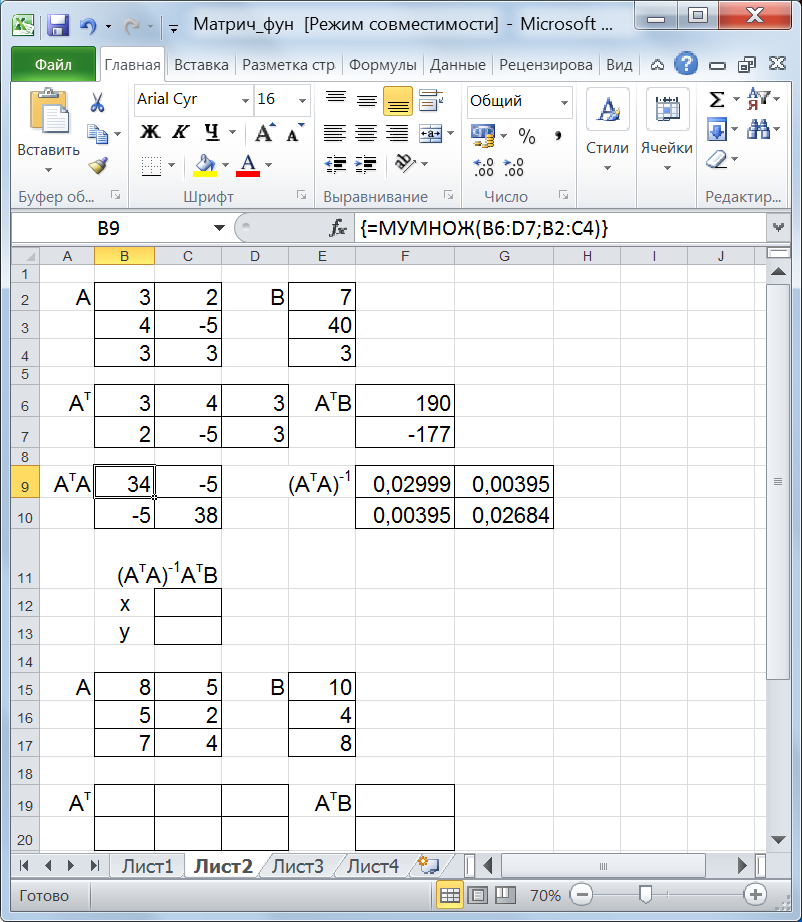
Рис. 24. Исходные данные задачи и определитель матрицы

Пример 4.5.Решите систему уравнений методом наименьших квадратов:

3х + 2у = 7

4х – 5у = 40

3х + 3у = 3

Решение. Для решения задачи на листе Excel введем матрицу А и вектор В и выделим пустые диапазоны для транспонированной матрицы (если диапазон исходной матрица А размерности n x m, то диапазон транспонированной матрицы имеет размерность mxn) и произведения А^TB (рис. 25).

Рис. 25. Исходные данные задачи и предварительные заготовки

Выделим диапазон В6:D7, вызовем встроенную функцию ТРАНСП (категория ссылки и массивы), где в качестве массива укажем матрицу А (диапазон В2:С4) и нажмем сочетание Shift+Ctrl+Enter. В диапазоне F6:F7, используя функцию МУМНОЖ, найдем произведение матриц А^TB. Далее в диапазоне В9:С10 необходимо найти произведение А^TАи в диапазоне F9:G10 обратную матрицу к этому произведению: (А^TА)^-1 (функция МОБР) (рис. 26).

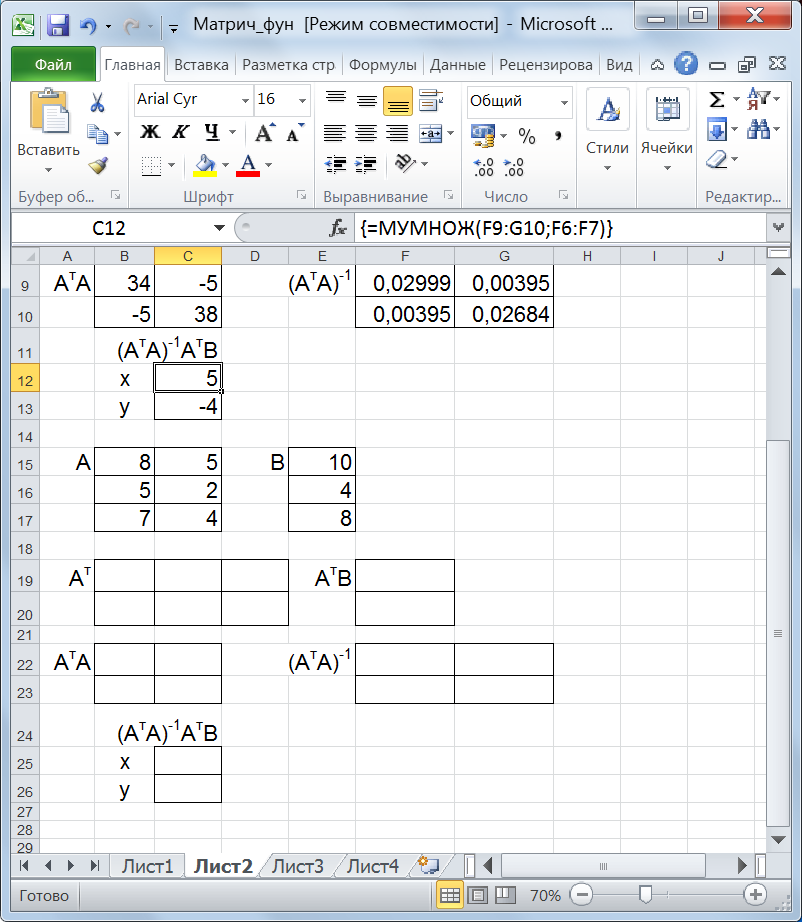
Рис. 26. Поэтапное решение задачи

Осталось найти произведение (А^TА)^-1А^TB, т.е. перемножить массивы из диапазонов F9:G10 и F6:F7, это и будет решением системы (рис. 27).

Рис. 27. Решение системы уравнений

Пример 4.6. В таблице приведены данные о дневной производительности пяти предприятий холдинга, выпускающих четыре вида продукции с использованием трех видов сырья, а также продолжительность работы каждого предприятия в году и цена каждого вида сырья.

Таблица 17.

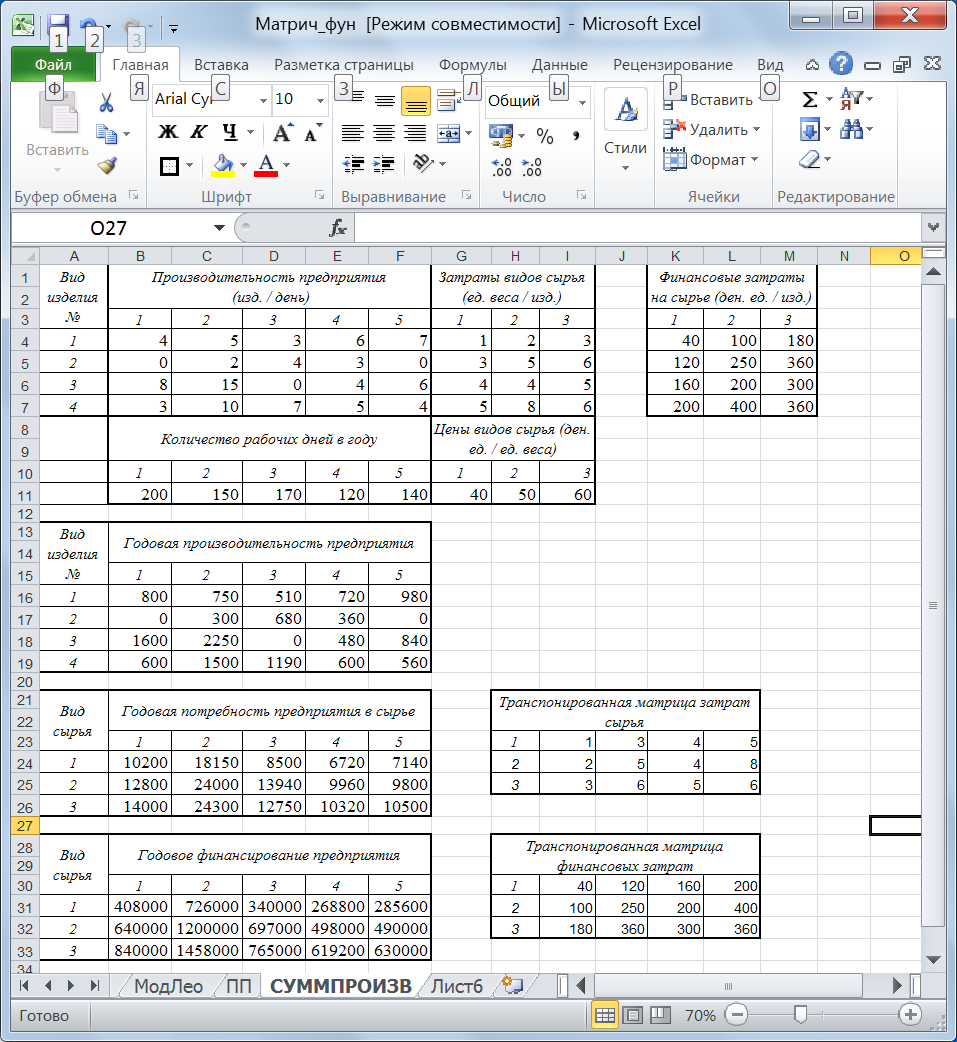
Требуется определить: годовую производительность каждого предприятия по каждому виду изделий; годовую потребность каждого предприятия в каждом виде сырья; годовую сумму финансирования каждого предприятия холдинга для закупки сырья, необходимого для выпуска продукции.

Решение. Перенесем исходные данные на лист Excel. Компьютерная модель задачи имеет вид (рис. 28).

Для расчета годовой производительности каждого предприятия необходимо найти произведение количества произведенных изделий в день каждым предприятием на количество рабочих дней в году каждого предприятия. Для этого выделим весь диапазон В16:F19 и введем формулу: =B4:F7*B11:F11, закончив ее ввод сочетанием клавиш Shift+Ctrl+Enter.

Аналогично рассчитаем матрицу финансовых затрат на каждый вид сырья для каждого изделия (диапазон (K4:М7): {=G4:I7*G11:I11}).

Для расчета годовой потребности каждого предприятия в каждом виде сырья необходимо найти сумму произведений годового выпуска каждого изделия на затраты каждого вида сырья на единицу изделия. Для этого транспонируем матрицу затрат видов сырья. Для первого изделия в диапазоне В24:В26 найдем произведение полученной транспонированной матрицы (диапазон I23:L25) на вектор годовой производительности первого предприятия (диапазон В16:В19). Формулу скопируем вправо для расчета годовой потребности в сырье других предприятий (в диалоговом окне функции МУМНОЖ не забудьте закрепить общий для всех диапазонI23:L25!).

Аналогично рассчитаем годовое финансирование для каждого предприятия на закупку сырья предварительно транспонировав в диапазоне I30:L32 матрицу финансовых затрат на сырье (диапазон К4:М7). Результаты всех расчетов приведены на рис. 28.

Пример 4.7.Известно, что рациональное функционирование многоотраслевого хозяйства предполагает соблюдение баланса между отраслями. Каждая отрасль многоотраслевого хозяйства является, с одной стороны, производителем определенной продукции, а с другой – потребителем продукции, выпускаемой другими отраслями. Макроэкономика функционирования многоотраслевого хозяйства требует, чтобы соблюдался баланс по производству и потреблению между отдельными отраслями.

Балансовый принцип связи различных отраслей состоит в том, что валовой выпуск i-й отрасли должен быть равен сумме объемов потребления. В простейшей форме балансовые соотношения имеют вид:

x_i = x_i1 + x_i2+ … + x_in + y_i , i = 1, 2, …, n,

где x_i— общий объем выпускаемой продукции i-й отрасли;

x_ij — объем продукции i-й отрасли, потребляемый j-й отраслью при производстве объема продукции x_j;

y_i — объем продукции i-й отрасли конечного потребления (для реализации в непроизводственной сфере). Сюда относятся личное потребление граждан, удовлетворение общественных потребностей, содержание государственных институтов и т.д.

Для производства продукции j-й отрасли объемом x_iнужно использовать продукцию i-й отрасли объемом a_ijx_i, где а_ij — постоянное число, характеризующее прямые затраты.

Это допущение позволяет представить модель многоотраслевой экономики (модель Леонтьева) в виде системы линейных уравнений, которая в матричной форме имеет вид Х= AХ + Y, (А= П/X^T, П{Х_ij} –матрица потребления, т.е. a_ij= Х_ij/ Х_i),

где X— вектор валового выпуска;

Y— вектор объема продукции конечного потребления;

A— матрица прямых затрат.

Приведенная система уравнений может быть представлена в виде

(E – A)X= Y,где E— единичная матрица.

Если существует обратная матрица (E – A)^–1 (матрица полных затрат), то существует единственное решение системы X= (E – A)^–1Y.

В таблице приведены данные об исполнении баланса за отчетный период (у.е.):                                                                                                       Таблица 18.

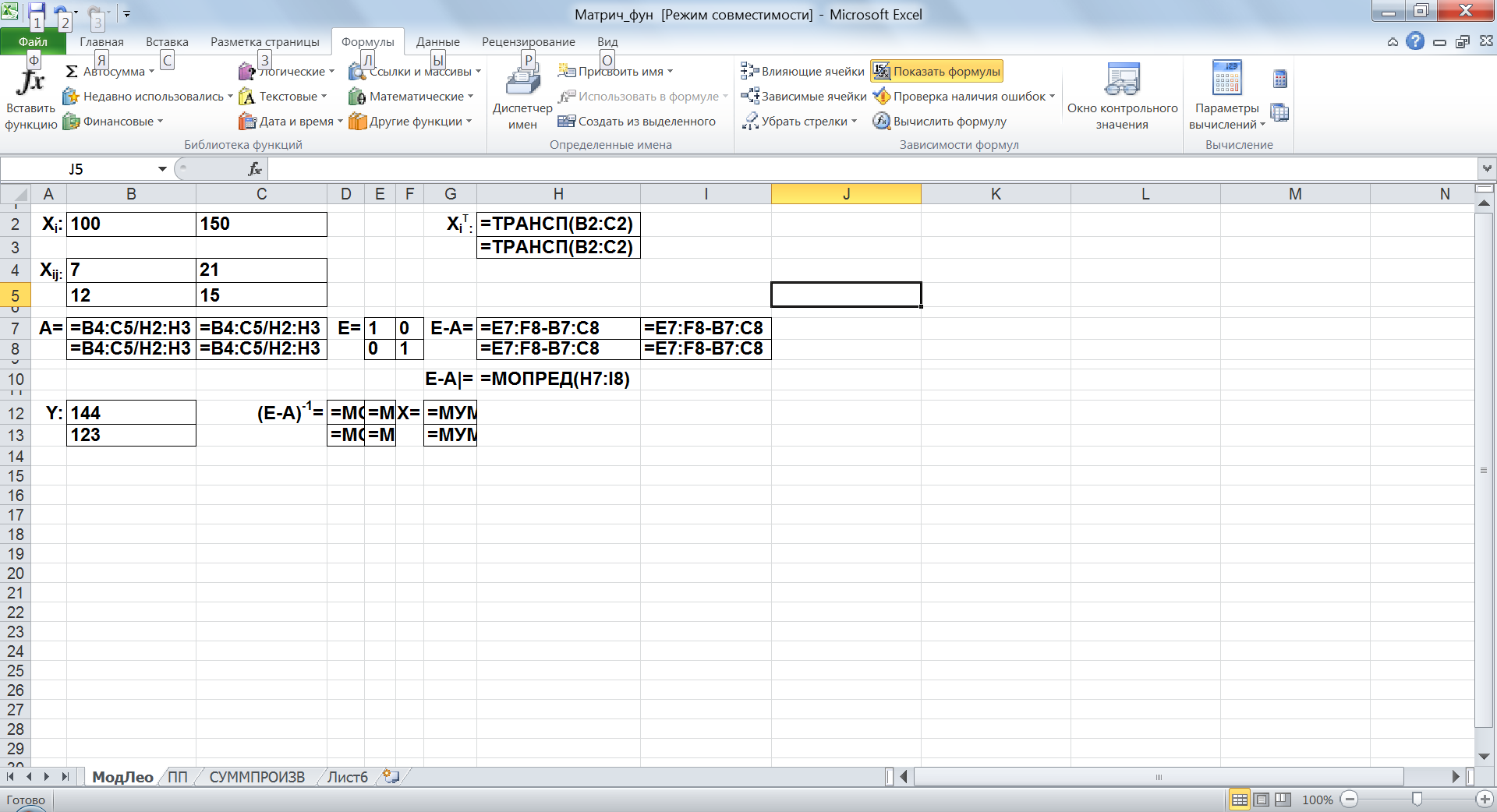
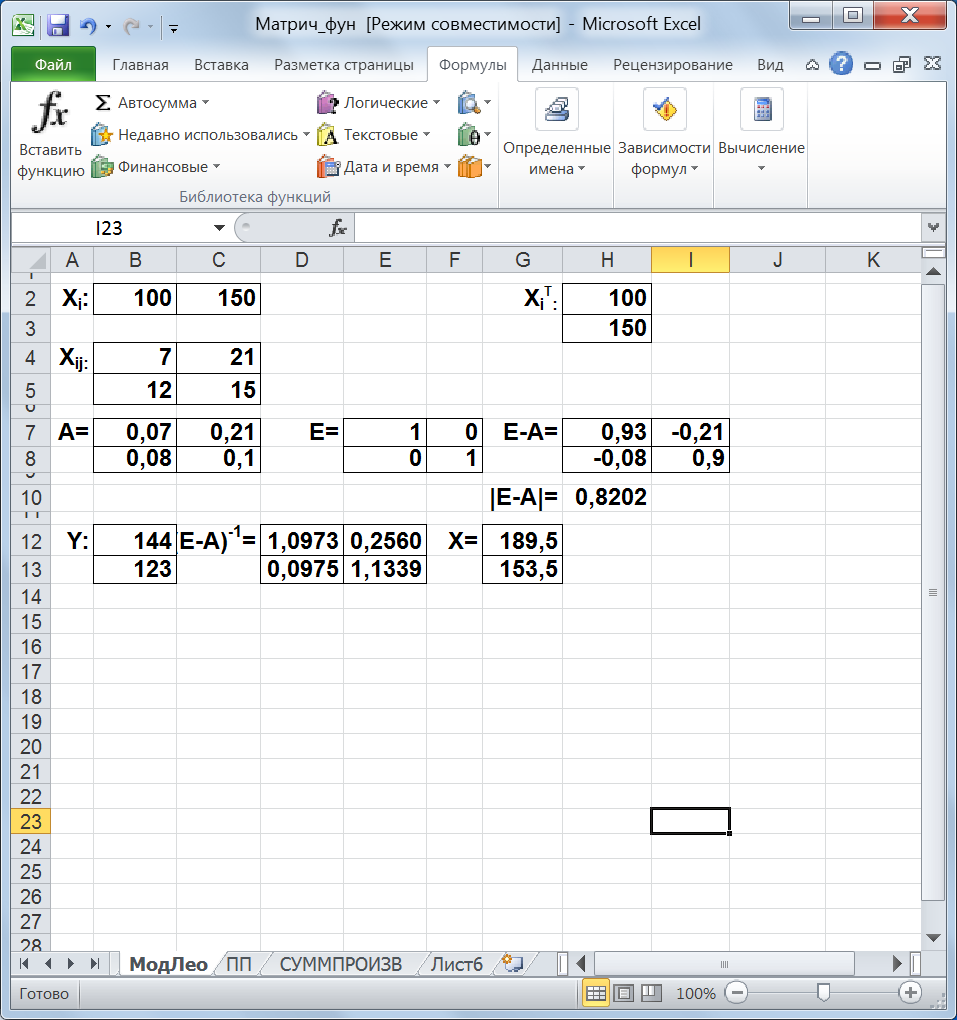
Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление I-ой отрасли увеличится вдвое, а II-ой сохранится на прежнем уровне.

Решение. На листе Excel разместим вектор X_i, матрицы X_ij, Е, новый вектор Y, а также свободные диапазоны для матриц X_i^T,А, (E-A), (E-A)^-1 и результирующего вектора Х. Рассчитаем матрицы А и Е-А по формулам, представленным на рис. 29.

Определитель матрицы |Е-А| = 0,8202 ≠ 0, так что обратная матрица и решение указанной системы уравнений существуют. Найдем его с использованием встроенных функций МОБР и МУМНОЖ (рис. 30).

Таким образом, согласно рис. 2, в I-ой отрасли валовой выпуск надо увеличить до 189,5 у.е., а во II-ой — до 153,5 у.е.

Рис. 29. Формулы расчетов матриц А и Е-А

Рис. 30. Решение балансовых экономических моделей