
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение систем линейных уравнений с помощью матричных функцийСистема m линейных уравнений с n неизвестными имеет вид: а11 + а12 + … + а1n = b1, а21 + а22 + … + а2n = b2, ……………….. am1 + аm2 + … + аmn = bm, где аij и bi, – коэффициенты при неизвестных и свободные члены. Если коэффициенты при неизвестных представить в виде матрицы А = Х = А-1В. Для решения таких систем используют матричные функции. Матричные функции Матричные функции используют для решения систем уравнений размерности nxn, т.е. когда число уравнений в системе равно числу неизвестных: функция МОПРЕД(массив) возвращает определитель матрицы; функция МОБР(массив) служит для нахождения обратной матрицы; функция МУМНОЖ(массив1; массив2) возвращает произведение матриц. Для нахождения определителя матрицы выделите свободную ячейку, вызовите встроенную функцию МОПРЕД, где в качестве массива укажите диапазон ячеек с исходной матрицей, нажмите ОК. Результат вычисления появится в выделенной ячейке. Для нахождения обратной матрицы выделите пустой диапазон такого же размера, как и исходная матрица, вызовите функцию МОБР, где в качестве массива укажите диапазон ячеек с исходной матрицей, нажмите сочетание клавиш Shift+Ctrl+Enter. В выделенном диапазоне отобразится обратная матрица.  Нахождение произведения матрицы А на матрицу В возможно, если число столбцов матрицы А равно числу строк матрицы В. Для нахождения произведения матриц выделите пустой диапазон такого же размера, как и исходная матрица В, вызовите функцию МУМНОЖ, где в качестве массива1 укажите диапазон ячеек с исходной матрицей А, в качестве массива2 – диапазон ячеек с матрицей В и нажмите сочетание клавиш Shift+Ctrl+Enter. В выделенном диапазоне отобразится результат умножения матриц. Над диапазонами, также как и над числами, можно производить арифметические операции, только в этом случае завершаться операция должна не нажатием клавиши Enter, а нажатием сочетания клавиш Shift+Ctrl+Enter!
Решение систем линейных уравнений методом Крамера Для решения системы уравненийметодом Крамера необходимо вычислить определитель исходной матрицы и определители частных матриц, полученных заменой i-го столбца на вектор свободных членов. Для нахождения вектора Х необходимо найти отношения частных определителей к общему, т.е. хj = Dj/D.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 431. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
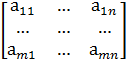 , а свободные члены и неизвестные в виде матриц-векторов В =
, а свободные члены и неизвестные в виде матриц-векторов В = 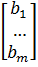 иX =
иX = 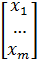 , то в матричном виде система линейных уравнений можно записать как АХ=В. Если обе части этого равенства умножить слева на матрицу А-1, то равенство не изменится и примет вид: А-1АХ = А-1В. Произведение А-1А даст единичную матрицу, которую можно опустить, таким образом, Х = А-1В, т.е. для нахождения неизвестного вектора Х необходимо найти обратную к А матрицу и перемножить ее с В:
, то в матричном виде система линейных уравнений можно записать как АХ=В. Если обе части этого равенства умножить слева на матрицу А-1, то равенство не изменится и примет вид: А-1АХ = А-1В. Произведение А-1А даст единичную матрицу, которую можно опустить, таким образом, Х = А-1В, т.е. для нахождения неизвестного вектора Х необходимо найти обратную к А матрицу и перемножить ее с В: