
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Построение модели парной линейной регрессииПрогнозировать изучаемые процессы можно с помощью регрессионных моделей. Наиболее простая из них – это модель парной линейной регрессии, которая имеет следующий вид:
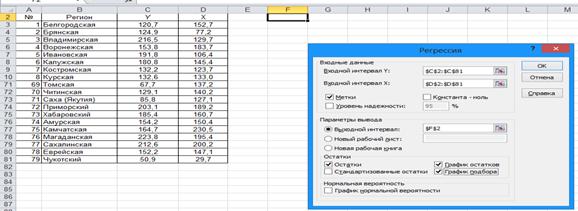
Где b0 – свободный член уравнения, отражающий влияние всех неучтенных факторов; b1 – коэффициент при факторе x. Суть построения модели сводится к определению параметров уравнения (b0, b1). В Excel построение этой модели осуществляется следующим образом: 1. Команда СЕРВИС – АНАЛИЗ ДАННЫХ – РЕГРЕССИЯ. 2. Ввести параметры окна (рис. 47). 3. ОК.
Рисунок 47. Ввод параметров окна при построении парной регрессии
Наиболее наглядно сравнение наблюдаемых и полученных с помощью модели значений иллюстрируется графиком подбора (рис. 48).
Рисунок 48. Соотношение модельных и эмпирических значений Y Таблица 1
В данном случае регрессионное уравнение будет иметь вид: Интерпретировать это уравнение можно следующим образом: при увеличении среднедушевых инвестиций в экономику региона на 1 р. (Х) среднедушевые доходы населения (Y) возрастут в среднем на 8 к., при отсутствии влияния прочих факторов. Качество модели в целом можно оценить множественным коэффициентом детерминации (R-квадрат), который для пары признаков Y и X равен:  Таким образом, можно сделать вывод, что 1 % изменчивости результативного признака Y объясняется изменчивостью признака X, то есть доля объясненной дисперсии результативного признака (Y) фактором (Х) равна 41 %, что является достаточно хорошим результатом, учитывая однофакторность модели. Этот результат подтверждается данными табл. 2, где в строке R-квадрат показано число 0,41, при умножении которого на 100 получаем множественный коэффициент детерминации. Таблица 2
Учитывая стохастическую природу построенной модели, необходимо оценить полученное уравнение регрессии с помощью средней ошибки аппроксимации и F-критерия Фишера, а статистическую значимость его параметров – с помощью t-критерия Стьюдента. Найдем среднюю относительную ошибку аппроксимации по формуле:
Для вычисления согласно формуле (3.17) составим таблицу, фрагмент которой показан на рис. 49 в режиме формул и рис. 50 в режиме значений. Здесь в столбце J определяется сумма абсолютных относительных ошибок, а в ячейке К25 - сама средняя относительная ошибка аппроксимации.
Рисунок 49. Фрагмент таблицы расчета средней относительной ошибки аппроксимации в режиме формул
Рисунок 50. Фрагмент таблицы расчета средней относительной ошибки аппроксимации в режиме значений В нашем примере Решим задачу: определить первые пять регионов, имеющих наибольшее отклонение значений моделируемого признака от среднестатистического. Решение: 1. В результате построения регрессионной модели имеем таблицу остатков (рис. 51).
Рисунок 51. Таблица остатков 2. Выделяем ее и назначаем режим автофильтра: Данные – Фильтр – Авто – фильтр. 3. В поле Остатки назначаем режим Первые 10…, вводим соответствующие параметры (рис. 52):
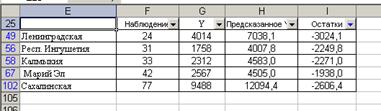
Рисунок 52. Назначение условий поиска В результате получаем пять субъектов Федерации, имеющих наибольшее положительное отклонение от среднестатистического значения (рис. 53), т. е. в рамках построенной модели у этих регионов среднедушевые доходы необоснованно высоки.
Рисунок 53. Субъекты Федерации, у которых высокие уровни среднедушевых доходов не обусловлены существующим уровнем инвестиционной активности Список же регионов с высоким потенциалом уровня среднедушевых доходов получим, выбрав условие «Первые пять – наименьших» (рис. 54).
Рисунок 54. Субъекты Федерации, у которых согласно построенной модели уровни среднедушевых доходов должны быть выше при существующем уровне инвестиционной активности
Если же остаток равен нулю, то уровень среднедушевых доходов в регионе соответствует среднестатистическому в рамках построенной модели. Однако такой случай в приведенном примере не наблюдался. Наибольшее соответствие эмпирического значения среднедушевых доходов с оценкой, полученной с помощью модели, у Ярославской области. Исследование статистической значимости уравнения регрессии в целом проводится с помощью F-критерия Фишера-Снедекора. Прежде всего, выдвигается гипотеза Н0 о том, что уравнение в целом статистически незначимо, при конкурирующей гипотезе Н1: уравнение в целом статистически значимо. Расчетное значение критерия находится по формуле:
Для уравнения парной регрессии p = 1. Пример получения количественной оценки F-критерия, согласно формуле (3.18), показан в таблице (рис. 55).
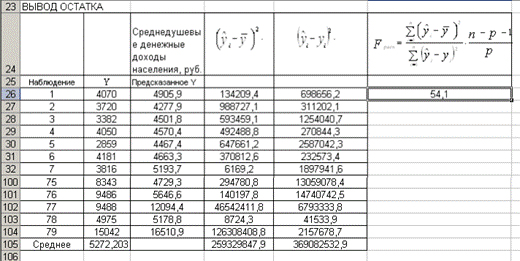
Рисунок 55. Фрагмент таблицы для расчета количественной оценки F-критерия в режиме формул В режиме значений таблица получения количественной оценки F-критерия показана на рис. 56.
Рисунок 56. Фрагмент таблицы для расчета количественной оценки F-критерия в режиме значений Табличное (теоретическое) значение критерия находится по таблице критических значений распределения Фишера-Снедекора по уровню значимости α и двум числам степеней свободы (k1 = p = 1 и k2 = n – p – 1 = 79 – 1 – 1 = 77):
Если Fрасч < Fтабл, то гипотеза Н0 принимается, а уравнение линейной регрессии в целом считается статистически незначимым (с вероятностью ошибки 5 %). Для уравнения (3.15) Fрасч = 54,1, то есть неравенство не выполняется, следовательно, гипотеза Н0 отвергается. Делаем вывод, что построенная регрессионная модель в целом статистически значима. Кроме оценки статистической модели в целом, необходимо проверить статистическую значимость оценок всех параметров (b0, b1) линейного уравнения. Осуществляется это с помощью t-критерия Стьюдента. Выдвигается гипотеза Н0: параметр bj = 0 (j = 0, 1) (статистически незначим, случайно отличается от 0), при конкурирующей гипотезе Н1: параметр bj ≠ 0 (статистически значим, не случайно отличается от 0). Находится расчетное значение критерия Стьюдента:
где средняя квадратическая ошибка для параметра b0 равна:
А для параметра b1:
Расчет этих оценок показан в таблице в режиме формул на рис. 57, а в режиме значений – на рис. 58.
Рисунок 57. Фрагмент таблицы в режиме формул для расчета средних квадратических ошибок для параметров b0 и b1
Рисунок 58. Фрагмент таблицы в режиме значений для расчета средних квадратических ошибок для параметров b0 и b1 Зная mi, можно определить расчетное значение критерия Стьюдента: Для Для
Теоретическое значение критерия tтабл. находится по таблице критических значений распределения Стьюдента по уровню значимости α и числу степеней свободы k = n – p – 1. Если tbj > tтабл., то гипотеза Н0 отвергается с вероятностью ошибки α, т. е. оценка коэффициента регрессии bj признается статистически значимой, в противном случае (tbj< tтабл.) – незначимой. Табличное значение критерия для уровня значимости α = 0,05 и числа степеней свободы k = n – 2 = 79 – 2 = 77 равно: tтабл. = 2,0.
Найдем доверительные интервалы для параметров b0 и b1 уравнения (1): ∆b0= tтабл. · mb0 = 2,0 · 311,15 = 622,30; ∆b1 = tтабл · mb1 = 2,0 · 0,010 632 5 = 0,021 265. Следовательно, нижняя граница доверительного интервала для b0 равна: b0 b0 = 3 873,837 9 – 622,3 = 3 251,54. Верхняя граница доверительного интервала для b0 равна: b0 b0 = 3 873,837 9 + 622,3 = 4 496,14. Нижняя граница доверительного интервала для b1 равна: b1 - Db1 =0,078 206 92- 0,021 265 = 0,056 9 Верхняя граница доверительного интервала для b1 равна: B1 + Db1 = 0,078 206 92+ 0,0212 65 = 0,099
Таблица 3 Проверка критерия Стьюдента
В результате проверки на статистическую значимость уравнения в целом, а также каждого его параметра можно сделать вывод о статистической его значимости, то есть построенная модель адекватно отражает рассматриваемое явление. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 455. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
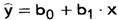 (3.14)
(3.14)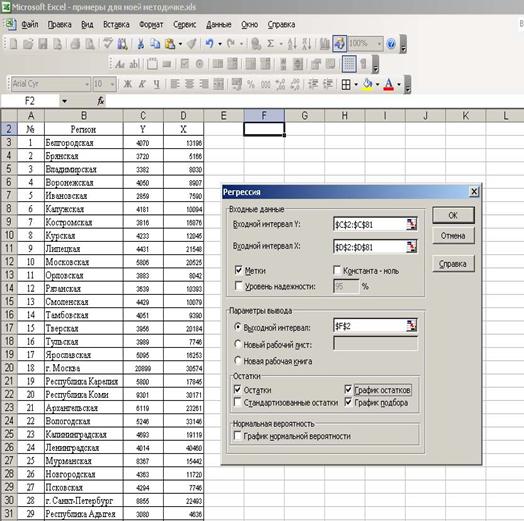

 (3.15)
(3.15) (3.16)
(3.16)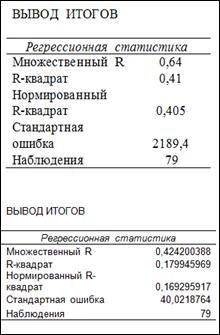
 (3.17)
(3.17)


 = 24,1 %, т. к. значения средней относительной ошибки аппроксимации немногим более 20 %, то можно точность уравнения определить как недостаточно высокую. В этом случае возникает вопрос, какие регионы имеют наибольшее отклонение от среднестатистического уровня, определенного с помощью модели. Осуществим эту задачу с помощью автофильтра.
= 24,1 %, т. к. значения средней относительной ошибки аппроксимации немногим более 20 %, то можно точность уравнения определить как недостаточно высокую. В этом случае возникает вопрос, какие регионы имеют наибольшее отклонение от среднестатистического уровня, определенного с помощью модели. Осуществим эту задачу с помощью автофильтра.


 (3.18)
(3.18)









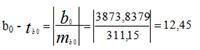

 = 3 873,838 + 0,078 × X
= 3 873,838 + 0,078 × X