
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Фильтрация дискретных сигналовПомехоустойчивость приёма дискретных сигналов, как это было показано выше, определяется отношением сигнал / помеха на входе решающего устрой-ства. Наибольшее отношение сигнал / помеха, равное отношению энергии элемента сигнала к спектральной плотности флуктуационной помехи Известно, что амплитудно-частотная характеристика оптимального фильтра для приёма дискретных сигналов совпадает с точностью до постоянного множителя C1 с амплитудным спектром сигнала K(w) = C1× S(w), а импульсная характеристика представляет собой зеркальное отображение временной функции сигнала, задержанное на длительность сигнала Т. Для прямоугольного радиоимпульса в качестве оптимального фильтра может быть использован колебательный контур высокой добротности, для которого динамическая амплитудно-частотная характеристика определяется выражением а эффективная полоса пропускания равна Dfэф = 1/ T. Амплитудно-частотная характеристика фильтра, оптимального для прямоугольного видеоимпульса, определяется выражением а эффективная полоса пропускания равна Dfэф = 1/ 2T. Иногда оптимальные фильтры трудно реализуемы. В этом случае применяют так называемые квазиоптимальные фильтры, амплитудно-частотная характеристика которых может иметь произвольную форму (ближе к прямоугольной). Эффективную полосу пропускания квазиоптимального фильтра выбирают такой, чтобы при данной форме его амплитудно-частотной характеристики обеспечивалось максимально возможное отношение сигнал/шум на выходе.  Для прямоугольного радиоимпульса максимум отношения сигнал / шум обеспечивается при ширине полосы пропускания квазиоптимального фильтра Dfэф, равной: - при использовании идеального полосового фильтра (с прямоугольной амплитудно-частотной характеристикой)
- при использовании одиночного параллельного колебательного контура
Энергетический проигрыш в отношении сигнал / шум при использовании вышеуказанных квазиоптимальных фильтров вместо оптимальных не превышает 18¸19 %. При приёме непрерывной последовательности импульсов ширина полосы пропускания квазиоптимального фильтра должна быть примерно в два-три раза больше, чем для одиночного импульса. Это объясняется тем, что кроме флуктуационных помех на помехоустойчивость приёма последовательности импульсов оказывает влияние также и межсимвольная интерференция (взаимное наложение импульсов на выходе фильтра). В этом случае полосу пропускания выбирают из условия минимизации на выходе фильтра суммы флуктуационной помехи и межсимвольной интерференции. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 608. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 , обеспечивают так называемые оптимальные фильтры.
, обеспечивают так называемые оптимальные фильтры. , (2.19)
, (2.19)
 , (2.20)
, (2.20) при этом
при этом 
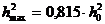 ,
, .
.