
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ОСНОВНЫЕ СООТНОШЕНИЯ
2.1 Оптимальный приём двоичных сигналов.Постановка задачи Важным показателем систем связи является помехоустойчивость, т.е. способность системы связи противостоять вредному влиянию помех. При рассмотрении вопросов передачи и приёма двоичных последовательностей полагают, что источник дискретных сообщений вырабатывает на своём выходе последовательность двух элементов (символов) – единицы и нуля с соответствующими вероятностями их появления p(1)и p(0). Для их передачи используют два различных сигнала S1(t) и S2(t), длительность каждого из которых равна длительности элемента последовательности Т. На вход приёмного устройства поступает смесь переданного сигнала и помехи, т. е.
Z(t) = Si (t) + x (t).
В курсовой работе рассматривается канал с постоянными параметрами и аддитивной помехой типа гауссовского белого шума. Такие (гауссовские) каналы являются достаточно хорошей моделью многих реальных каналов передачи цифровой информации, в частности, кабельных, оптических, радиорелейных, космических и других. Для количественной оценки влияния помех и других факторов, вызывающих отличие принятой последовательности от переданной, вводится критерий оценки качества принятой информации. При передаче дискретных сообщений за такой критерий принимают вероятность ошибки приёма одного элемента двоичной последовательности. Приёмник, в результате анализа принятой конкретной реализации Z(t) на интервале времени 0 £ t £ T , должен установить, какой из возможных сигналов Si (t) (S1(t) или S2(t)) присутствует на его входе, и в соответствии с этим принять решение о приеме символа 1 или 0. Это классическая задача теории связи – задача различения двух сигналов. В случае, когда один из сигналов тождественно равен нулю (например, ДАМ), имеем задачу обнаружения сигнала в интервале времени 0 £ t £ T на фоне помех.  Для различения сигналов в приёмнике необходимо (с допустимой погрешностью) устанавливать начало и конец интервала анализа каждой реализации Z(t), поступающей на вход приёмника. Такая задача решается устройством синхронизации, которое позволяет определять начало и окончание каждого элемента сигнала (сообщения) в принятой последовательности. Алгоритм различения двух и более сигналов на фоне белого гауссовского шума имеет ясный физический смысл: наиболее вероятным переданным сигналом считается тот сигнал, который меньше отличается (в среднеквадратичном смысле) от принятого сигнала. Таким образом, оптимальный приемник минимизирует среднюю вероятность ошибки. В аналитической форме алгоритм оптимального приёмника при равновероятных сигналах имеет вид
Если
т.е. решение принимается в пользу сигнала S1(t). При этом считается, что все параметры сигнала в точке приёма известны, т. е. известны его форма, амплитуда, частота, задержка во времени и начальная фаза (приём полностью известных сигналов). Неизвестным в этом случае является только то, какой из возможных сигналов передаётся на данном интервале Выражение (2.1) позволяет представить алгоритм в виде структурной схемы оптимального приёмника, т. е. решить задачу оптимального синтеза. Для передачи элементов двоичного кода (0 или 1) обычно используются сигналы с дискретной амплитудной модуляцией (ДАМ), частотной модуляцией (ДЧМ) и фазовой модуляцией (ДФМ или ДОФМ). Для конкретного вида используемых сигналов ДАМ, ДЧМ, ДФМ алгоритм оптимального приёмника и соответствующая ему структурная схема получаются на основании общего алгоритма (2.1), при этом оптимальный приёмник должен вычислять значение функции взаимной корреляции вида
Для этого используется или коррелятор, или согласованный фильтр, которые обеспечивают одинаковую помехоустойчивость, т. е. эквивалентны. В процессе передачи элементы кода искажаются помехами, причем, наблюдаются ошибки двоякого рода: 1 При передаче элемента 0 может быть ошибочно принят элемент 1, вероятность такого события (перехода 0®1) обозначим через p(1/0) — вероятность приема 1 при передаче 0. 2 При передаче элемента 1 может быть ошибочно принят элемент 0, вероятность такого события (перехода 1®0) обозначим через p(0/1) — вероятность приема 0 при передаче 1. Средняя вероятность ошибки определяется по формуле
pош = p(0)× p(1/0) + p(1)× p(0/1). (2.3)
В дальнейшем будем считать, что априорные вероятности передачи элементов кода равны, то есть p(0) = p(1) = 0,5, при этом
pош = 0,5[p(1/0) + p(0/1)]. (2.4)
Помеху в канале связи будем считать флуктуационной с нормальным законом распределения мгновенных значений
w (x) =
Вероятность ошибки зависит: от вида модуляции, способа детектирования (когерентный, некогерентный), способа фильтрации сигналов в приёмнике (оптимальный фильтр, неоптимальный фильтр), мощности Pс (энергии Eс) сигнала, мощности Pп (спектральной плотности N0) помехи. Если в приёмнике используется неоптимальный фильтр, вероятность ошибки зависит от величины отношения мощности сигнала к мощности помехи (отношение сигнал/шум по мощности) h2 = Pс / Pп.
В приёмнике с оптимальным фильтром отношение сигнал/шум больше, чем в приёмнике с неоптимальным фильтром и, соответственно, помехоустойчивость выше. Приёмник с оптимальным фильтром и когерентным способом приёма обеспечивает потенциальную помехоустойчивость для заданного вида модуляции. Помехоустойчивость приема сигналов ДАМ, ДЧМ, ДФМ, ДОФМ в указанных выше условиях можно определить, вычисляя среднюю вероятность ошибки следующим образом.
2.2 Дискретная амплитудная модуляция Элементами сигналов ДАМ являются посылки (кодовый элемент «1») и паузы (кодовый элемент «0»)
где Т – длительность элемента сигнала.
Некогерентный прием Прием сигнала ДАМ в этом случае осуществляется путем сравнения уровня сигнала после амплитудного детектора (детектора огибающей) с некоторым пороговым уровнем Uп решающей схемы приемника (рис. 2). Ошибки возникают в случаях: 1 При передаче посылки огибающая суммы сигнала и помехи (Eсп) оказывается меньше порогового уровня Uп (переход 1®0). 2 При передаче паузы огибающая помехи Eп оказывается больше Uп (переход 0®1). Вероятности этих событий определяются через соответствующие распределения значений огибающих (рис. 3,а и рис 3,б)
где w(Eсп)– плотность распределения огибающей суммы сигнала и помехи, которая, как известно, определяется обобщенным законом Релея (Релея-Райса),
w(Eп) – плотность распределения огибающей помехи, определяется простым законом Релея.
Средняя вероятность ошибки с учетом (2.4) и (2.6) равна pошАМнкг = 0,5
Значение pош зависит от порогового уровня Uп решающей схемы. Можно показать, что вероятность ошибки минимальна, когда Uп
где Ф(z) – табулированный интеграл вероятностей. Зависимость pош = f(h) при некогерентном приеме показана на рис. 5 (кривая 1). Если h2 » 1, то pош.АМ нкг »
Максимальная помехоустойчивость при приеме сигналов ДАМ наблюдается в том случае, если применяется оптимальная фильтрация сигналов. В этом случае необходимо в ф-ле (2.9) вместо
где N0 – спектральная плотность мощности помехи.
Когерентный прием
где w(x/a) и w(x)-плотности распределения вероятностей мгновенных значений сигналов на выходе детектора при приёме посылки и паузы соответственно
Средняя вероятность ошибки будет равна
pошАМкг = 0,5
При оптимальном значении порогового уровня решающей схемы pошАМкг = где Зависимость pошАМ = f(h) при когерентном приёме показана на рис. 6 (кривая 2). При когерентном приеме достигается потенциальная помехоустойчивость, если в приемнике осуществить оптимальную фильтрацию сигнала. При этом достигается максимальное отношение сигнал /шум
и в ф-ле (2.11) h заменяется на h0.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 413. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
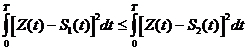 , то Z(t) º S1(t), иначе S2(t), (2.1)
, то Z(t) º S1(t), иначе S2(t), (2.1) . (2.2)
. (2.2) .
.  (2.5)
(2.5) При использовании в приёмнике оптимального фильтра вероятность ошибки определяется величиной отношения энергии элемента сигнала к спектральной плотности мощности помехи h02 = Eс / N0 = PсTс/ N0.
При использовании в приёмнике оптимального фильтра вероятность ошибки определяется величиной отношения энергии элемента сигнала к спектральной плотности мощности помехи h02 = Eс / N0 = PсTс/ N0. 0 £ t £ T,
0 £ t £ T, , (2.6)
, (2.6) ,
,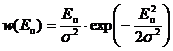 .
.
 . (2.7)
. (2.7) (при a2 » s2), т.е в этом случае Uп имеет оптимальное значение. При этом окончательно получаем
(при a2 » s2), т.е в этом случае Uп имеет оптимальное значение. При этом окончательно получаем , (2.8)
, (2.8) – отношение мощностей сигнала и помехи (отношение сигнал / шум), а
– отношение мощностей сигнала и помехи (отношение сигнал / шум), а
 . (2.9)
. (2.9) подставить
подставить  , равное
, равное , (2.10)
, (2.10) – энергия элемента сигнала,
– энергия элемента сигнала,
 При когерентном приеме применяется синхронный детектор, который устраняет влияние ортогональной составляющей вектора помехи (рис. 2). Составляющая x=Eп·cosj имеет нормальный закон распределения и мощность
При когерентном приеме применяется синхронный детектор, который устраняет влияние ортогональной составляющей вектора помехи (рис. 2). Составляющая x=Eп·cosj имеет нормальный закон распределения и мощность  . Поэтому вероятность искажения посылки р(0/1) и вероятность искажения паузы р(1/0) будут равны (рис. 4)
. Поэтому вероятность искажения посылки р(0/1) и вероятность искажения паузы р(1/0) будут равны (рис. 4)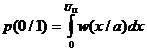 и
и  ,
,  и
и  .
. .
. , вероятность ошибки минимальна и равна
, вероятность ошибки минимальна и равна , (2.11)
, (2.11) – отношение сигнал / шум.
– отношение сигнал / шум. ,
,