
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Этап 5. Спектральный анализ временного ряда. Оценка сезонных колебаний. Оценка точности прогнозирования уровня показателя. ⇐ ПредыдущаяСтр 4 из 4
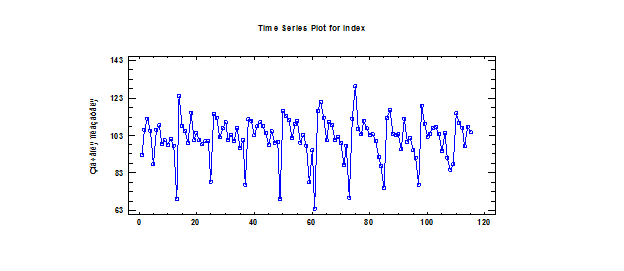
Исследуемый показатель – индекс производства резиновых и пластмассовых изделий (в % к предыдущему году). Что можно сразу сказать, глядя на этот график, так это то, что у временного ряда 100% есть сезонность? Что касается тренда, то здесь нужно сделать ряд проверок, чтобы убедиться в его наличии или отсутствии. Проверка ряда на стационарность. Гипотеза о равенстве дисперсий.
Ratio of Variances = 0,778771 F-test to Compare Standard Deviations Null hypothesis: sigma1 = sigma2 Alt. hypothesis: sigma1 NE sigma2 F = 0,778771 P-value = 0,405531 Do not reject the null hypothesis for alpha = 0,05. Так как P-value>0,05, гипотеза о равенстве дисперсий не отвергается, то есть исследуемый временной ряд стационарен, и тренд в нем отсутствует. Гипотеза о равенстве средних. Проверим, постоянна ли средняя на всем временном ряду или нет. Было принято решение разделить выборку в соотношении 1/3 и 2/3. Результаты представлены ниже.
Null hypothesis: mean1 = mean2 Alt. hypothesis: mean1 NE mean2 assuming equal variances: t = -0,111237 P-value = 0,911626 Do not reject the null hypothesis for alpha = 0,05. Так как P-value >0,05, гипотеза о равенстве средних не отвергается, то есть средние равны на всем интервале, что говорит в пользу стационарности и отсутствия тренда в модели! Анализ автокорреляционных функций.
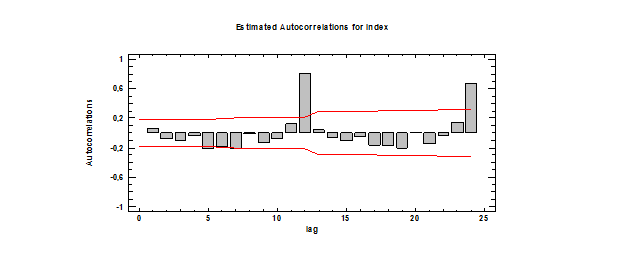
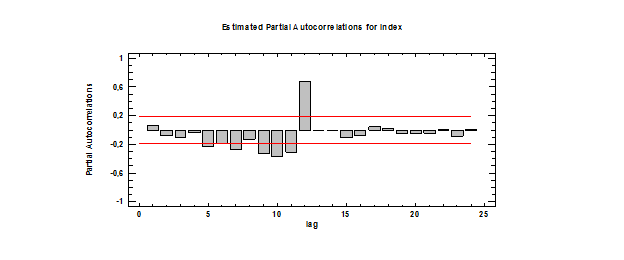
Из графика автокорреляционной функции явно бросается в глаза цикличность (которую как раз можно интерпретировать как сезонность); на ЧАКФе это менее заметно. Эти функции иллюстрируют нестационарность процесса как факт наличия сезонности, закономерности во временном ряде.  Проверка ряда на случайность. Проведем 3 теста на случайность элементов временного ряда. Расчет критерия серий по медиане выборки. Нулевая гипотеза – ряд случаен. Альтернативная ряд не случаен. Runs above and below median Median = 103,3 Number of runs above and below median = 48 Expected number of runs = 57,4956 Large sample test statistic z = 1,70021 P-value = 0,0890918 Так как P-value>0,05, можно сделать вывод о том, что элементы ряда случайны. Расчет критерия восходящих и нисходящих серий. Нулевая гипотеза – ряд случаен. Альтернативная ряд не случаен. Runs up and down Number of runs up and down = 74 Expected number of runs = 76,3333 Large sample test statistic z = 0,408699 P-value = 0,682757 Так как P-value>0,05, можно сделать вывод о том, что элементы ряда случайны. Тест Бокса-Пирса Нулевая гипотеза – нет значимых автокорреляций до 24 шага. Альтернативная гипотеза – есть значимые автокорреляции до 24 шага Test based on first 24 autocorrelations Large sample test statistic = 166,065 P-value = 0,0 P-value<0,05, значит, по этому тесту элементы временного ряда неслучайны. Итог: 1 тест из 3 показал неслучайность элементов временного ряда, что говорит о нестационарности моделируемого процесса в целом и отсутствия трендовой составляющей. Чтобы окончательно убедиться в том, что тренда в исследуемом временном ряде нет, построим периодограмму и посмотрим, что она будет из себя представлять.
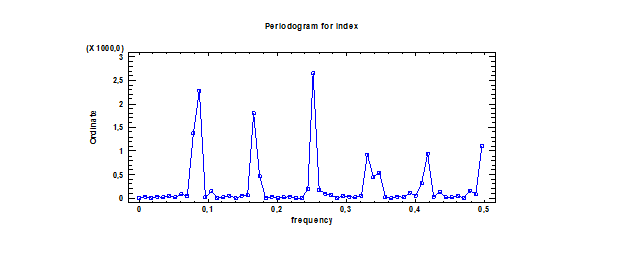
По периодограмме видно, что временной ряд «очищен» от тренда, так как на графике изображены систематические колебания, а не резкий пик в начале, после которого все идет на спад (так было бы, если бы во временном ряду присутствовал тренд). Все это говорит о том, что можно приступать к моделированию сезонности непосредственно с самого спектрального анализа. Для начала определим m (предполагаемый период изменений): по таблице, отображающей значения периодограммы получается, что m=3,96;
Такое значение m связано с тем, что последний год (2013) в выборке представлен не полностью, а только 5 месяцами, то есть не полностью: чтобы не искажать этим картину, необходимо убрать последние 5 значений из выборки и перестроить периодограмму. Получилось следующее:
Здесь значение m получилось равным 12 (на этот период приходится самая большая ордината). h=n/m = 108/12=9; j=m/2=12/2=6; Воспользовавшись методом НМК, получаем следующие параметры модели и их значимость по t-статистике:
По t-статистике вышло, что один коэффициент вышел незначимым (
По гармоникам вышло, что все коэффициенты значимы – решено было все их оставить и по ним строить прогноз. Итоговая модель имеет следующий вид: Y(t) =101,54 – 7,45cos( А прогноз с прогнозными интервалами следующий:
Выводы: Из всех модельных значений наихудшим значением оказалось за январь 2013 – фактическое значение даже не попало в границы прогнозного интервала, во всем остальном прогноз получился очень даже хорошим, особенно на февраль 2013 года (там самое маленькое отклонение получилось). Этап 4.Сглаживание временного ряда с использованием авторегрессионной модели. Оценка точности прогнозирования уровня показателя. Проверим временной ряд на стационарность при помощи расширенного теста Дикки-Фуллера. Результаты представлены ниже: Тест Дики-Фуллера (GLS) для Y объем выборки 111 нулевая гипотеза единичного корня: a = 1
с константой и трендом модель: (1-L)y = b0 + b1*t + (a-1)*y(-1) + e коэф. автокорреляции 1-го порядка для e: 0,005 оценка для (a - 1): -0,839008 тестовая статистика: tau = -8,91146
10% 5% 2,5% 1% Крит. значения: -2,64 -2,93 -3,18 -3,46
Регрессия теста Дики-Фуллера МНК, использованы наблюдения 3-113 (T = 111) Зависимая переменная: d_yd
Коэффициент Ст. ошибка t-статистика P-значение --------------------------------------------------------------- yd_1 -0,839008 0,0941493 -8,911 NA
Крит. Акаике: 3960,04 Крит. Шварца: 3962,75 Крит. Хеннана-Куинна: 3961,14 Так как в результате получили, что | Также параметр Исходя из всего этого d (степень интегрирования)=0; Теперь построим ARIMA-модели с разными параметрами, чтобы максимально уменьшить RMSE. Models (A) ARIMA(1,0,1) (B) ARIMA(1,0,0) with constant (C) ARIMA(2,0,1) (D) ARIMA(1,1,1) with constant (E) ARIMA(1,0,2) Estimation Period
Выводы: наилучшей моделью по полученным данным является модель В) - ARIMA(1,0,0) with constant: у этой модели самая низкая среднеквадратическая ошибка, самая низкая средняя ошибка прогноза, самая низкая средняя абсолютная ошибкам прогноза, средняя процентная абсолютная ошибка прогноза. Несмотря на все это, это не самая удачная модель для прогноза, потому что AR у нее не значим:
Зато у модели А) ARIMA(1,0,1) все параметры получились значимыми, несмотря на то, что она далеко не первая и не вторая по прогностическим характеристикам:
ARIMA Model Summary
Прогноз и интервал:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 571. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

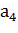 ). Проверим значимость коэффициентов по гармоникам!
). Проверим значимость коэффициентов по гармоникам!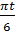 )+2,87sin(
)+2,87sin( 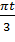 )-0,6sin(
)-0,6sin(  )-6,15sin(
)-6,15sin(  )-3,72sin(
)-3,72sin( 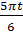 )-1,74sin(
)-1,74sin( 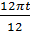 );
); | < 1, следовательно, нулевая гипотеза о наличии единичного корняне отвергается, а, следовательно, исходный ряд стационарен относительно стохастического тренда.
| < 1, следовательно, нулевая гипотеза о наличии единичного корняне отвергается, а, следовательно, исходный ряд стационарен относительно стохастического тренда. получился отрицательным и по модулю меньше единицы. Можно сказать, что временной ряд относится к классу TSP (с детерминированным трендом).
получился отрицательным и по модулю меньше единицы. Можно сказать, что временной ряд относится к классу TSP (с детерминированным трендом).