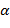Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчет критерия серий по медиане выборки.Нулевая гипотеза – ряд случаен. Альтернативная ряд не случаен. Runs above and below median Median = -2,70943E6 Number of runs above and below median = 43 Expected number of runs = 57,0 Large sample test statistic z = 2,56283 P-value = 0,0103823 Так как P-value<0,05, можно сделать вывод о том, что элементы ряда неслучайны. Runs up and down Нулевая гипотеза – ряд случаен. Альтернативная ряд не случаен. Number of runs up and down = 62 Expected number of runs = 75,0 Large sample test statistic z = 2,81153 P-value = 0,0049307 Так как P-value<0,05, можно сделать вывод о том, что элементы ряда неслучайны. Box-PierceTest Альтернативная гипотеза – есть значимые автокорреляции до 24 шага. Test based on first 24 autocorrelations Large sample test statistic = 16,0973 P-value = 0,884533 P-value>0,05, значит, элементы ряда случайны. Выводы: так как 2 из 3 тестов показали неслучайность остатков, логично сделать вывод о том, что выбранная в данном этапе модель непригодна для построения прогнозов. Этап 2. Сглаживание модельного ряда с использование модели Брауна. Оценка точности прогнозирования уровня показателя. Результаты моделирования с помощью экспоненциального сглаживания представлены ниже:
Если посмотреть по полученным данным, то выходит, что самая лучшая модель, это модель с параметром сглаживания =0,1 ( у нее самый маленький коэффициент Тейла и самая маленькая среднеквадратическая ошибка).
Ее прогноз на 114 наблюдение и интервалы для прогноза:
Фактическое значение - 68716972,00.  Протестируем остатки выбранной модели на случайность: Автокорреляционная функция и частная автокорреляционная функция
По графикам значения автокорреляционной функций не выходят за границы, значит, по этому критерию, остатки соответствуют «белому шуму». Проведем тесты на случайность остатков, чтобы убедиться (или не убедиться) в том, что остатки случайны. Расчет критерия серий по медиане выборки. Нулевая гипотеза – ряд случаен. Альтернативная ряд не случаен. Runs above and below median Median = -2,09821E6 Number of runs above and below median = 48 Expected number of runs = 57,0 Large sample test statistic z = 1,61363 P-value = 0,106606 Так как P-value>0,05, то по этому тесту остатки случайны. Расчет критерия восходящих и нисходящих серий. Нулевая гипотеза – ряд случаен. Альтернативная ряд не случаен. Runs up and down Number of runs up and down = 62 Expected number of runs = 75,0 Large sample test statistic z = 2,81153 P-value = 0,0049307 P-value<0,05, значит, по этому тесту остатки неслучайны. Тест Бокса-Пирса Нулевая гипотеза – нет значимых автокорреляций до 24 шага. Альтернативная гипотеза – есть значимые автокорреляции до 24 шага Box-Pierce Test Test based on first 24 autocorrelations Large sample test statistic = 18,6045 P-value = 0,772741 Так как P-value>0,05, то по этому тесту остатки случайны. Итог: 1 тест из 3-х показал, что остатки неслучайны, значит, остатки не соответствуют «белому шуму» и по выбранной модели строить прогноз некорректно. |
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 361. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |