
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПП в цепях с двумя накопителямиСтр 1 из 4Следующая ⇒ ОПЕРАТОРНЫЙ МЕТОД РАСЧЁТА ПП Основные теоретические положения Сущность операторного метода заключается в том, что от некоторой функции вещественного переменного (например, времени t), называемой оригиналом f(t), переходят к функции комплексного переменного f(р), называемой изображением. При этом дифуравнения относительно оригиналов превращаются в алгебраические уравнения относительно изображений, решение которых проще. Изображение и оригинал функции связывают формулой прямого преобразования Лапласа f(р) = В справочной литературе имеются таблицы оригиналов и соответствующих им изображений. Изображения наиболее характерных оригиналов приведены в табл. 7.3. Таблица 7.3
Закон Ома для последовательного участка R-L-C: I(р) = где Z(р) = R + pL + В числителе кроме изображения напряжения на зажимах участка U(р) фигурируют внутренние операторные ЭДС LiL(0) и I закон Кирхгофа: для любого узла S ±I(р) = 0. II закон Кирхгофа: для любого контура
Поскольку законы Ома и Кирхгофа в операторной форме имеют такой же вид, как и в цепях постоянного тока (ЦПТ), то все методы анализа ЦПТ, основанные на этих законах, могут быть применены для анализа операторных схем с учётом независимых начальных условий. По изображениям искомых величин, полученным в результате анализа операторной схемы, находят оригиналы искомых величин. Для этого применяют обратное преобразование Лапласа или используют таблицу преобразований Лапласа, или пользуются теоремой разложения. В последнем случае изображение искомой величины приводят к виду:  f(р) = где f1(р) и f2(р) – степенные многочлены: f1(р) = bm pm + bm-1 pm-1 + … + b1 p + b0, f2(р) = an pn + an-1 pn-1 + … + a1 p + a0, причём m £ n и дробь несократима (числитель и знаменатель не имеют одинаковых корней). Оригинал определяется по формулам:
где pk – корни уравнения f2(р) = 0, а n – число корней этого уравнения, f1(рk) и f2¢(рk) – значения многочлена f1(р) и производной от многочлена f2(р) при k-м корне. В случае пары комплексных сопряжённых корней можно использовать следующие формулы: или Рекомендуемая последовательность расчёта ПП операторным методом. 1. Расчётом цепи до коммутации определяют независимые начальные условия iL(0), uC(0) и записывают величины внутренних операторных ЭДС LiL(0) и 2. Для цепи после коммутации составляется эквивалентная операторная схема. 3. Любым методом анализа ЦПТ определяют изображения требуемых токов и напряжений, приводя затем их к виду рациональной дроби. 4. По теореме разложения или с помощью обратных преобразований Лапласа находят оригиналы искомых токов и напряжений переходного процесса.
ПП в цепях с одним накопителем
u(t) = 30t2 + 18t + 10 В. Параметры цепи: r1 = r2 = = 100 Ом, С = 10 мкФ. Рассчитать ток конденсатора. Решение До появления напряжения на источнике цепь находилась в состоянии покоя. Поэтому данная задача – с нулевыми начальными условиями, а эквивалентная операторная схема выглядит так, как на рис. 7.68,б. Изображение приложенного напряжения определяем, используя таблицу преобразований Лапласа: U(p) = Изображения первого и третьего токов: I1(p) = I3(p) = = Разложим последнее выражение на простые дроби: I3(p) = Приведя в выражениях для I3(p) дроби к общему знаменателю и приравняв числители, получим следующее уравнение: Ар(рr1r2C + r1 + r2) + B(рr1r2C + r1 + r2) + Dp2 = 60r2C + р×18r2C + р2×10r2C. Приравниваем коэффициенты при одинаковых степенях р и получаем систему уравнений: коэффициенты при p2 : АСr1r2 + D = 10r2C; при p : А(r1 + r2) + ВСr1r2 = 18r2C; при 1 : В(r1 + r2) = 60r2C. Отсюда В = А = D = 10r2C – АСr1r2 = 0,01 – 9×10 –5×10 –5×10 4 = 0,01. Окончательно получаем: I3(p) =
Задача 7.46. В приведенной на рис. 7.69,а схеме рассчитать напряжение и ток индуктивности. Числовые значения: u = 24 В, L = 0,25 Гн, r1= 30 Ом, r2= 10 Ом. Решение 1. Рассчитаем независимое начальное условие и запишем величину внутренней операторной ЭДС: iL(0+) = iL(0-) = LiL(0+) = 0,25·2,4 = 0,6 В·с. 2. Эквивалентная операторная схема приведена на рис. 7.69,б. 3. Поскольку обе операторные ЭДС оказались в одной ветви, изображе-ние тока IL(p) определим по закону Ома: IL(p) = = На основании второго закона Кирхгофа UL(p) = рL·IL(p) – LiL(0) = рL· = 4. Оригинал тока iL(t) определим с помощью теоремы разложения: iL(t) = Корень уравнения F2(p) = p + 30 = 0 – p = -30 c -1, производная F2¢(p) = 1, F2(0) = 30; F1(0) = 96, F1(p) = 96 – 30·2,4 = 24; iL(t) = Изображение напряжения на индуктивности UL(p) = uL(t) =6е -30t B.
Задача7.47. В схеме рис. 7.70,а рассчитать ток i2(t) и напряжение на ёмкости uС(t), если u = 240 В, Е3 = 100 В, r1= r3= 50 Ом, С = 1000 мкФ. Решение 1. Независимое начальное условие: uС(0+) = uС(0-) = -Е3 = -100 В. Внутренняя операторная ЭДС 2. Операторная схема замещения представлена на рис. 7.70,б. 3. Поскольку по условию задачи требуется рассчитать только один ток, то его изображение определим методом эквивалентного генератора (рис. 7.70,в). По второму закону Кирхгофа: UХХ(р) + r1·IХ(р) = По закону Ома IХ(р) = Тогда UХХ(р) = Входное сопротивление схемы относительно разомкнутых зажимов ZBХ(р) = Изображение искомого тока I2(p): I2(p) = На основании второго закона Кирхгофа UС(р) – Отсюда UС(р) = 4. Оригинал тока найдём по таблице преобразований Лапласа: i2(t) = 6,8е -40t А. Оригинал напряжения найдём с помощью теоремы разложения: корень уравнения F2(p) = p + 40 = 0 – p = -40 c -1,
F1(0) = 2800, F1(p) = -100·(-40) + 2800 = 6800; uС(t) =
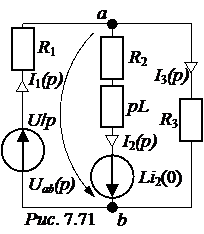
ЗАДАЧА 7.48. Решить задачу 7.11 операторным методом. Ответы: i2(0) =0,8 A; эквивалентная опера-торная схема на рис. 7.71; Uab(p) = I1(p) = I2(p) = I3(p) = i1(t) = 2,5 – 0,346е -92,31t А; i2(t) = 1,25 – 0,45е -92,31t А; i3(t) = 1,25 + 0,104е -92,31t А. Задача7.49. Решить задачу 7.12 операторным методом.
I1(p) =
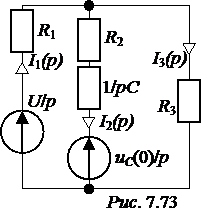
I3(p) = Задача7.50. Решить задачу 7.13 опера-торным методом. Ответы: uС(0) = 100 B, эквивалентная опера-торная схема на рис. 7.73; I1(p) = I2(p) = I3(p) = i1(t) = 0,667 – 0,167е -125t А; i2(t) = -0,25е -125t А; i3(t) = 0,667 + 0,083е -125t А.
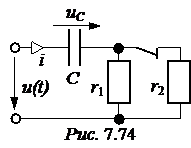
ЗАДАЧА 7.51. Рассчитать переходный про-цесс в схеме рис. 7.74 классическим и операторным методами: u(t) = 100×sin(200t + 90°) B, r1 = r2 = 100 Ом, С = 50 мкФ. Решение I. Расчёт классическим методом. 1. Получим независимое начальное условие uC(0) анализом цепи до коммутации: хC = Im = j = arctg yuC = yi – 90° = 153,4° – 90° = 63,4°, uC(t-) = 89,4×sin(200t + 63,4°) B, uC(0+) = uC(0-) = 89,4×sin63,4° = 80 B. Зависимое начальное условие (ток в цепи в момент сразу после коммутации): i(0) = 2. Рассчитаем принуждённые составляющие тока и напряжения на конденсаторе: Imпр = yiпр =yu – arctg yuCпр = yiпр – 90° = 135° – 90° = 45°, uCпр(t) = 70,7×sin(200t + 45°) B, iпр(t) = 0,707×sin(200t + 135°) A. Начальные значения принуждённых составляющих: uCпр(0) = 70,7×sin45° = 50 B, iпр(0) = 0,707×sin135° = 0,5 A. 3. Характеристическое уравнение и его корень:
4. Свободные составляющие: uCсв(t) = A×e рt, iсв(t) = В×e рt.
A = uCсв(0) = uC(0) – uCпр(0) = 80 – 50 = 30, В = iсв(0) = i(0) – iпр(0) = 0,2 – 0,5 = -0,3. 5. Окончательно получаем: uC(t) = uCпр(t) + uCсв(t) = 70,7×sin(200t + 45°) + 30×e -200t B, i(t) = iпр(t) + iсв(t) = 0,707×sin(200t + 135°) – 0,3×e -200t A. ii. Расчёт операторным методом. 1. Независимое начальное условие – uC(0+) = uC(0-) = 80 B. 2. Эквивалентная операторная схема на рис. 7.75. Изображение напряжения источника находим по прямому преобразованию Лапласа: u(t) = 100×sin(200t + 90°) 3. Изображение тока находим по закону Ома, причём с целью получения выражений, соответствующих таблице преобразований Лапласа, полученное выражение разложим на правильные дроби: I(p) = =
A + 0,005B = 0, B + 40000D = -160. Решение системы: А = 0,5; B = -100; D = -0,0015. Таким образом, I(p) = Первую дробь приведём к следующему табличному виду:
Возникает ещё одна система уравнений:
200×Мcosy = -100. Мcosy = -0,5. tgy = -1, y = 135°, М = 4. По таблице преобразований Лапласа находим ответ: i(t) = 0,707×sin(200t + 135°) – 0,3×e -200t A. iii. Следует отметить, что при синусоидальном источнике, напряжение или ток которого можно записать в комплексной форме, возможен и другой подход к нахождению изображений и оригиналов величин. Покажем его. Согласно символическому методу, синусоидальное напряжение равно мнимой части от комплексного мгновенного значения, записываемого в виде экспоненты. Но тогда и изображение напряжения источника может быть получено взятием мнимой части от изображения комплексного мгновенного значения: u(t) = Um×sin(wt +yu)= Im[Um×e j(wt + yu)]= Im[Ume jyu×e jwt] Изображение тока находим по закону Ома по схеме рис. 7.75: I(p) = Im = Im где F1(p) = pC(Ume jyu – juC(0)) – uC(0)wC, F2(p) = (p – jw)(r1Cp + 1). Оригинал тока найдём с помощью теоремы разложения. Для этого предварительно вычислим: - корни уравнения F2(p) = 0: p1 = jw = j200 с –1; p2 = - - F2¢(p) = 2r1Cp + 1 – jwr1C; F2¢(p1) = j + 1; F2¢(p2) = -1 – j; - F1(p1) = Ume jyujwC = 100×j×j×200×50×10 –6 = -1; - F1(p2) = -200(100j – j80)×50×10 –6 – 80×200×50×10 –6 = = -0,8 – j0,2 = 0,825×e –j166°. i(t) = Im
= 0,707×sin(200t + 135°) – 0,3×e -200t A.
iV. Наконец, операторным методом можно рассчитать только свободные составляющие тока и напряжения на конденсаторе, предварительно рассчитав принуждённые составляющие символическим методом (см. часть i настоящей задачи): iпр(t) = 0,707×sin(200t + 135°) A; uCпр(t) = 70,7×sin(200t + 45°) B, uCпр(0) = 70,7×sin45° = 50 B, uCсв(0) = uC(0) – uCпр(0) = 80 – 50 = 30 B. Эквивалентная операторная схема для свободного режима представлена на рис. 7.76. Полученная цепь рассчитывается на основании закона Ома, оригиналы величин находим, используя таблицу преобразований Лапласа. Iсв(p)= uCсв(p) = Iсв(p)× = =
r1= r2= 25 Ом, L = 0,1 Гн, J = 4 A. Ответы. I1(p) = i1(t) = -2 + 2sin(1000t – 78,5°) + 3,96e -500t A.
Задача7.53. В схеме рис. 7.78 r = 100 Ом, С = 10 мкФ, E0 = 300 В, e(t) = 100sin(1000t – 90°) В. Определить ток ПП. Ответы. uС(0) = -300 В, расчётная операторная схема идентична схеме рис. 7.75; e(t) = -Emcosw0t I(p) = p1,2= ± jw0 = ± j1000 c -1, p3= -1/(rC) = -1000 c -1; F2¢(p) = 2p(rpC + 1) + (p2 + w02)rC; i(t) = =
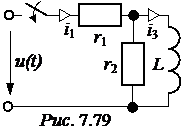
ЗАДАЧА 7.54. В схеме рис. 7.79 рассчитать токи i1(t) и i3(t), если u(t) = U0·e -at, U0 = 40 В, a = 20 c -1, r1= 5 Ом, r2= 10 Ом, L = 100 мГн. Ответы. U(p) = I1(p) = p1= -a = -20 c -1; p2=-33,33 c -1; F2¢(p) = (р + a)L(r1+ r2) + рL(r1+ r2) + r1·r2; i1(t) = I3(p) = I1(p)· ЗАДАЧА 7.55. Решить задачу 7.18 операторным методом. Решение Задачу решим, используя в качестве вычислительной техники MathCAD. Отметим, что в MathCAD в качестве операторной переменной р используется переменная s; единичная скачкообразная функция 1(t) Хевисайда обозначается Ф(t). Исходные данные: t := 0.6·10 -3 r1 := 20 r2 := 30 С := 5·10 -5. ЭДС источника в виде прямоугольного импульса, записанная с помощью функции Хевисайда: Е(t) := 100·(Ф(t) – Ф(t – t)). Изображение ЭДС: Е(t) Перезадаём ЭДС: ЕЕ(s) := Входное операторное сопротивление цепи: Z(s) := r1 + Изображения токов: i1(s) := Оригиналы токов: i1(s) i2(s) i3(s) Для построения графиков токов их нужно перезадать: i1(t) := 2.+3.·е (-1667.)·t – 2.·Ф(t –.6000е-3) – 3.·Ф(t –.6000е-3)·е (-1667.)·t+1 i2(t) := 2.–2.·е (-1667.)·t – 2.·Ф(t –.6000е-3) + 2.·Ф(t –.6000е-3)·е (-1667.)·t+1 i3(t) = 5.·е (-1667.)·t – 5.·Ф(t –.6000е-3)·е (-1667.)·t+1.
ЗАДАЧА 7.56. Решить за-дачу 7.19 операторным методом. Решение
С учётом сказанного, ЭДС источника записывается формулой: Е(t) := 100· Для контроля выведем график Е(t) (рис. 7.81). Изображение ЭДС представляется довольно длинной формулой, поэтому приводим её в уменьшенном виде:
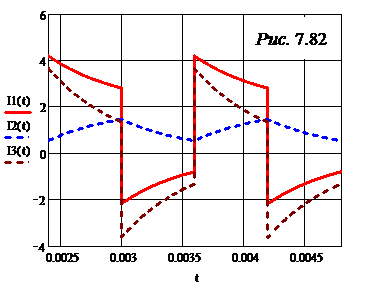
Перезадаём ЭДС:
Поскольку цепь та же, что и в задаче 7.55, формулы для входного сопротивления, изображений и оригиналов будут теми же, что и в задаче 7.55. Ответы для токов, по которым построены графики рис. 7.82, выглядят следующим образом: i1(t) :=2.+3.·е (-1667.)·t –2.·Ф(t–.6000е-3)–3.·Ф(t –.6000е-3)·е (-1667.)·t+1+ +2.·Ф(t–.1200е-2)+3.·Ф(t–.1200е-2)·е (-1667.)·t+2–2.·Ф(t–.1800е-2)–… i2(t) :=2.–2.·е (-1667.)·t –2.·Ф(t–.6000е-3) + 2.·Ф(t–.6000е-3)·е (-1667.)·t+1+ … i3(t) = 5.·е (-1667.)·t –5.·Ф(t–.6000е-3)·е (-1667.)·t+1+5.·Ф(t–.1200е-2)·е (-1667.)·t+2 …
На графиках рис. 7.82 рабочим участком является диапазон 0,0036 с £ t £ 0,0048 с.
ЗАДАЧА7.57. Задачу 7.22 решить операторным методом, используя способ расчёта установившейся реакции путём суммирования изображений реакций в области комплексного переменного. Решение Рассчитаем изображение по Лапласу первого импульса напряжения на интервале 0 £ t £ t0 U1(p) = Для определения изображения напряжения просуммируем n одинаковых импульсов, смещённых во времени на период T. Получим U(p) = U1(p)[1 + e -pT + e -2pT + … + e –(n-1)pT]. Для установившегося режима n ® ¥ U(p) = U1(p) = Изображение тока на n-м интервале при n ® ¥ I(p) = Полюс изображения, полученный из уравнения Z(p) = r + pL = 0, p1= -r/L = -t -1 = -25 c -1 определяет свободную составляющую тока, которая рассчитывается по теореме разложения iсв(t) = где F2¢(p1) = (p12+ w2)(1 – Тогда iсв = Заметим, что полученное выражение справедливо для любого (n+1)-го импульса при n ® ¥, 0 < t < ¥, если t отсчитывается от начала этого импульса, что непосредственно следует из определения оригинала: f(t) º 0 при t < 0. Из классического метода расчёта переходных процессов следует, что i = iпр + iсв, слагаемое iпр определяется видом приложенного к схеме напряжения: если это напряжение периодическое, то уже на интервале действия первого импульса есть слагаемое iпр = iуст – установившаяся реакция на периодическое воздействие. Таким образом, iуст = i(1)– iсв, где i(1)– ток переходного процесса в интервале действия первого импульса. Для рассматриваемого примера в интервале действия (n+1)-го импульса для t(0 … t0) получаем iуст(t) = Imsin(wt – j) + Imsinj · = Imsin(wt – j) – Imsinj в период паузы t(t0 … T) iуст(t) = A = 22,24 Как и следовало ожидать, полученные результаты совпадают с ранее вычисленными двумя разными методами. Отметим, что для контроля правильности решения задачи для периодического решения необходимо проверять условие, на котором базируется первый из рассмотренных методов: iуст(0) = iуст(T).
ПП в цепях с двумя накопителями
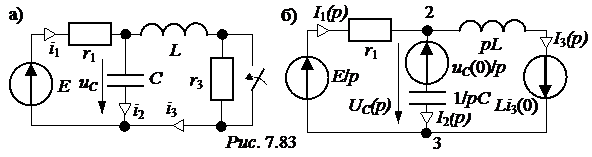
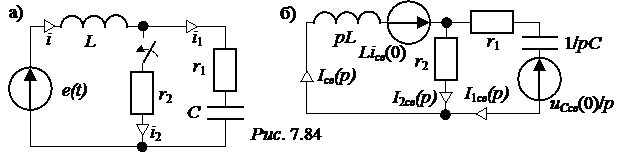
ЗАДАЧА7.58. В схеме рис. 7.83,а найти ток i3(t) и напряжение uС(t) операторным методом. Параметры цепи: Е = 300 В, r1 = r3 = 25 Ом, L = 0,02 Гн, С = 100 мкФ. Решение 1. Для построения операторной схемы определяем независимые начальные условия: i3(0+) = i3(0-) = uC(0+) = uC(0-) = r3·i3(0-) = 25·6 = 150 В. 2. Эквивалентная операторная схема показана на рис. 7.83,б. 3. Выполним расчёт схемы методом двух узлов. u23(p) = uC(p) = = I3(p) = 4. Оригиналы величин найдём по теореме разложения. Положим F2(p) = r1LCp2 + pL + r1 = 5·10 -5p2 + 0,02p + 25 = 0, корни уравнения р1,2 = -200 ± j678 c -1 = -706,9·e -j73,56°; F2(0) = 25; F2¢(p) = 10 -4p + 1; F2¢(p1) = j0,0678. Формула для напряжения на конденсаторе: uС(t) = 2Re F1U(p1) = 300·0,02 + 25·(-200 + j678)·0,02·10 -4·150 – 25·0,02·6 = 5,3·e j73,56°; uС(t) = 2Re = 156,3e -200tsin(678t + 73,56°) B. Рассчитываем ток i3(t) = F1i(0) = 300; F1i(p1) = 300 + 25·(-200 + j678)·10 -4·150 + + 6·(-200 + j678)·0,02·(25·(-200 + j678)·10 -4 + 1) = 265·e j73,56°; i3(t) = = 12 + 11,06e -200tsin(678t – 32,88°) А.
ЗАДАЧА7.59. В схеме рис. 7.84 определить ток i2(t) при следующих параметрах цепи: е(t) = Еmsin(w0t + y); Еm = 400 В, w0 = 100 рад/с, y = -45°; L = 0,25 Гн, С = 400 мкФ, r1 = 25 Ом, r2 = 75 Ом. Решение 1. Рассчитаем независимые начальные условия. Im = UCm = Im· i(t-) = 16sin(w0t – 45°) А; uC(t-) = 400sin(w0t – 135°) B; i(0+) = i(0-) = 16sin(-45°) = -8 2. Рассчитаем принуждённые составляющие iпр(t), i2пр(t) и uCпр(t) символическим методом. Imпр = I2mпр = Imпр· UCmпр = I1mпр· |
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 277. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
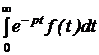 .
.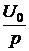 ,
, 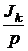 ,
, 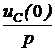
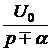 ,
, 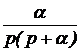
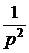 ,
, 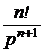 ,
, 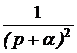
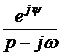
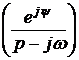 =
= 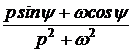
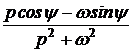
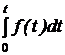
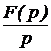
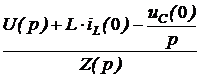 ,
, – операторное сопротивление этого участка.
– операторное сопротивление этого участка.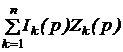 =
= 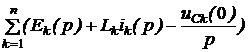 .
.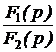 или
или 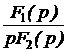 ,
,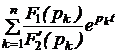 или
или 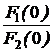 +
+ 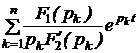 ,
,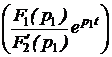
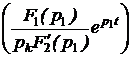 .
.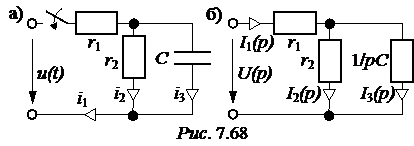 ЗАДАЧА 7.45. Напряжение, приложен-ное к цепи рис. 7.68,а изменяется по закону
ЗАДАЧА 7.45. Напряжение, приложен-ное к цепи рис. 7.68,а изменяется по закону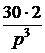 +
+ 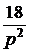 +
+ 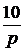 .
.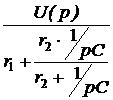 ;
; 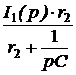 =
= 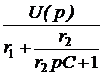 ×
× 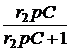 =
= 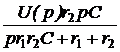 =
=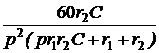 +
+ 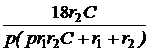 +
+ 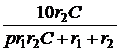 .
.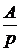 +
+ 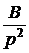 +
+ 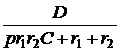 .
.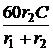 =
= 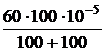 = 3×10 –4;
= 3×10 –4;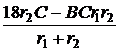 =
= 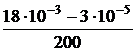 = 9×10 –5;
= 9×10 –5;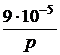 +
+ 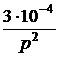 +
+ 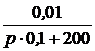
 9×10 –5 + 3×10 –4×t + 0,1×е -2000t А = i3(t).
9×10 –5 + 3×10 –4×t + 0,1×е -2000t А = i3(t).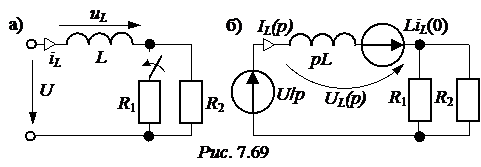
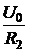 =
= 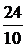 = 2,4 А,
= 2,4 А,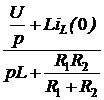 =
= 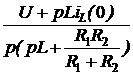 =
= 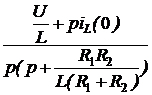 =
= 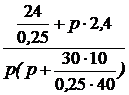 =
=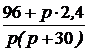 =
= 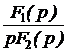 .
.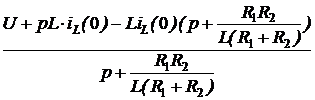 =
= 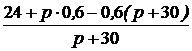 =
= 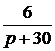 .
.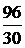 +
+ 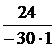 е -30t = 3,2 – 0,8е -30t А.
е -30t = 3,2 – 0,8е -30t А.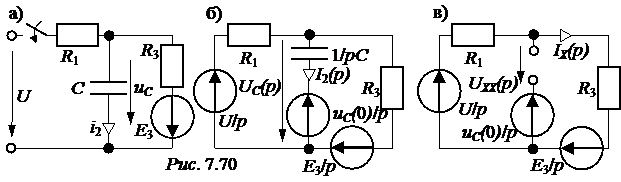
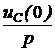 = -
= - 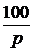 .
.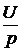 –
– 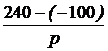 =
= 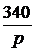 .
.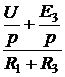 =
= 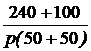 =
= 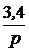 .
.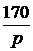 .
.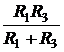 =
= 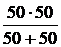 = 25 Ом.
= 25 Ом.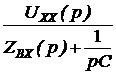 =
= 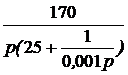 =
= 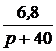 .
.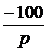 +
+ 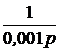 ·
· 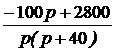 =
=  производная F2¢(p) = 1, F2(0) = 40;
производная F2¢(p) = 1, F2(0) = 40;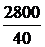 +
+ 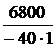 е -40t = 70 – 170е -40t В.
е -40t = 70 – 170е -40t В.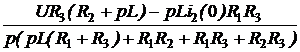 ;
;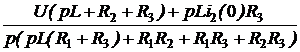 =
= 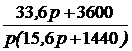 ;
;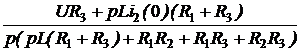 =
= 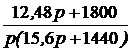 ;
; =
= 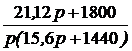 ;
;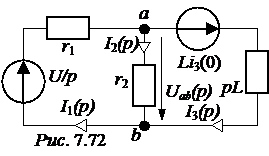 Ответы: независимое начальное условие – i3(0) = 1 А, эквивалентная опера-торная схема представлена на рис. 7.72; выражения для узлового напряжения и токов: Uab(p) =
Ответы: независимое начальное условие – i3(0) = 1 А, эквивалентная опера-торная схема представлена на рис. 7.72; выражения для узлового напряжения и токов: Uab(p) = 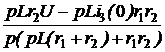 ;
;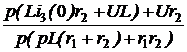
 I2(p) =
I2(p) = 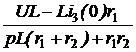
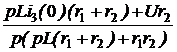
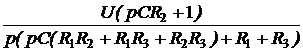 =
= 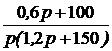 ;
;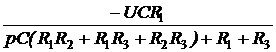 =
= 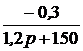 ;
;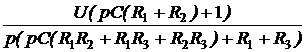 =
= 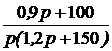 ;
;
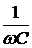 =
= 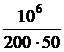 = 100 Ом, Z =
= 100 Ом, Z = 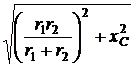 =
= 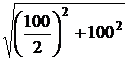 = 111,8 Ом,
= 111,8 Ом,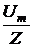 =
= 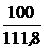 = 0,894 A, UCm = Im×хC = 0,894×100 = 89,4 B,
= 0,894 A, UCm = Im×хC = 0,894×100 = 89,4 B,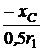 = -arctg
= -arctg 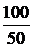 = -63,4°, yi =yu – j = 90° + 63,4° = 153,4°,
= -63,4°, yi =yu – j = 90° + 63,4° = 153,4°,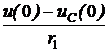 =
= 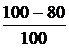 = 0,2 А.
= 0,2 А.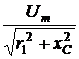 =
= 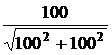 = 0,707 A, UCmпр = Imпр×хC = 0,707×100 = 70,7 B,
= 0,707 A, UCmпр = Imпр×хC = 0,707×100 = 70,7 B,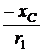 = 90° + arctg
= 90° + arctg 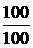 = 135°,
= 135°,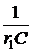 = -
= - 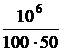 = -200 с -1.
= -200 с -1.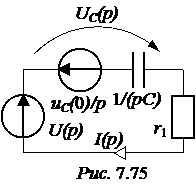 Постоянные интегрирования:
Постоянные интегрирования: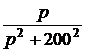 = u(p).
= u(p).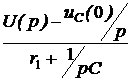 =
= 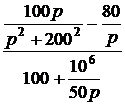 =
= 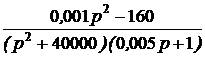 =
=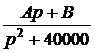 +
+ 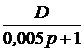 =
= 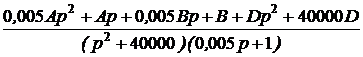 .
. Возникает следующая система уравнений: 0,005А + D = 0,001,
Возникает следующая система уравнений: 0,005А + D = 0,001,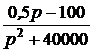 +
+ 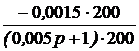 =
= 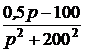 +
+ 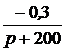 .
.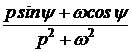 .
.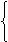
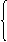 Мsiny = 0,5, Мsiny = 0,5,
Мsiny = 0,5, Мsiny = 0,5, 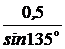 = 0,707.
= 0,707.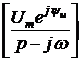 = U(p).
= U(p).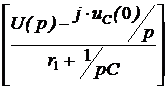 = Im
= Im 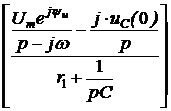 =
=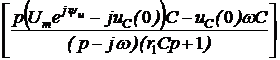 = Im
= Im 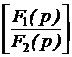 ,
,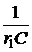 = -200 с –1;
= -200 с –1;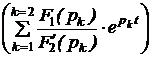 = Im
= Im 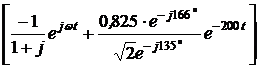 =
=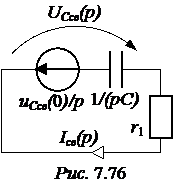 = Im
= Im 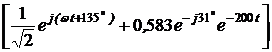 =
= 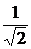 ×sin(wt +135°) – 0,583sin31°×e -200t =
×sin(wt +135°) – 0,583sin31°×e -200t =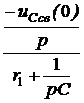 =
= 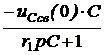 =
= 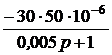 =
= 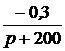
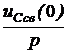 =
= 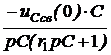 +
+ 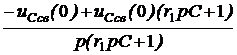 =
= 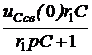 =
= 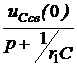 =
=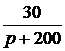
 ЗАДАЧА 7.52. В схеме рис. 7.77 найти ток i1(t), если e(t) = 100
ЗАДАЧА 7.52. В схеме рис. 7.77 найти ток i1(t), если e(t) = 100 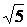 sin(1000t – 15°) В,
sin(1000t – 15°) В,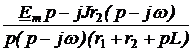 ;
;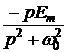 ;
;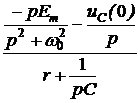 =
= 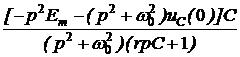 =
= 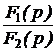 ;
;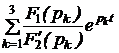 = 2Re
= 2Re 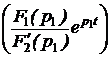 +
+ 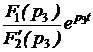 =
=
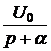 ;
;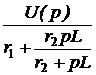 =
= 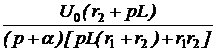 =
= 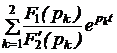 = 16e -20t – 13,33e -33,33t A;
= 16e -20t – 13,33e -33,33t A;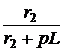 =
= 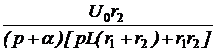 ; i3(t) = 20e -20t – 20e -33,33t A.
; i3(t) = 20e -20t – 20e -33,33t A.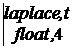 ®
® 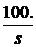 – 100·
– 100· 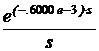 .
.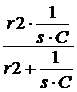 Z(s)
Z(s) 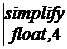 ® 20.·
® 20.· 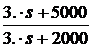 .
.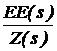 i2(s) := i1(s)·
i2(s) := i1(s)· 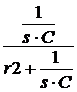 i3(s) := i1(s)·
i3(s) := i1(s)· 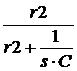 .
. ®2.+3.·е (-1667.)·t – 2.·Ф(t –.6000е-3) – 3.·Ф(t –.6000е-3)·е (-1667.)·t+1
®2.+3.·е (-1667.)·t – 2.·Ф(t –.6000е-3) – 3.·Ф(t –.6000е-3)·е (-1667.)·t+1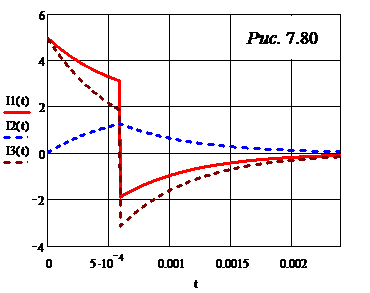 Полученные ответы для токов при необходимости путём некоторых преобразований могут быть приведены к виду ответов к задаче 7.18. Графики токов приведены на рис. 7.80.
Полученные ответы для токов при необходимости путём некоторых преобразований могут быть приведены к виду ответов к задаче 7.18. Графики токов приведены на рис. 7.80.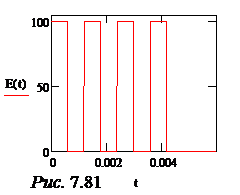 Примем, что прямоуголь-ные импульсы начинают посту-пать с момента времени t = 0. Это допущение необходимо в связи с тем, что преобразования Лапласа осуществляются только для t ³ 0. Период источника составляет, согласно условию, 2t. Поскольку учёт действия бесконечно большого числа импульсов источника вызывает затрудне-ния (см. задачу 7.57), рассмотрим их ограничен-ное количество. Так как практическая длитель-ность переходного процесса составляет 5t, то есть менее трёх периодов, достаточно учесть три периода (импульса) до начала расчётного (рабочего) периода, находящегося в диапазоне 3Т £ t £ 4Т.
Примем, что прямоуголь-ные импульсы начинают посту-пать с момента времени t = 0. Это допущение необходимо в связи с тем, что преобразования Лапласа осуществляются только для t ³ 0. Период источника составляет, согласно условию, 2t. Поскольку учёт действия бесконечно большого числа импульсов источника вызывает затрудне-ния (см. задачу 7.57), рассмотрим их ограничен-ное количество. Так как практическая длитель-ность переходного процесса составляет 5t, то есть менее трёх периодов, достаточно учесть три периода (импульса) до начала расчётного (рабочего) периода, находящегося в диапазоне 3Т £ t £ 4Т.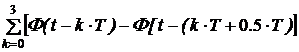 .
.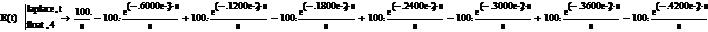
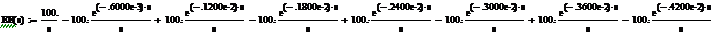
 У первого и второго токов в ответе содержится 16 слагаемых, у третьего – 8.
У первого и второго токов в ответе содержится 16 слагаемых, у третьего – 8.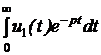 =
= 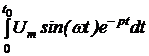 =
= 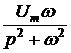 (1 +
(1 + 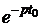 ).
).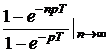 = U1(p)
= U1(p) 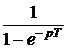 =
=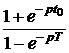 .
.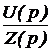 =
= 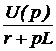 =
= 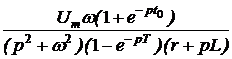 =
= 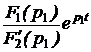 ,
,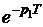 )L.
)L.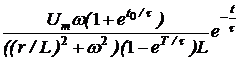 = Imsinj
= Imsinj 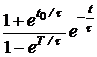 .
.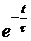 – Imsinj
– Imsinj 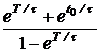 = 4,94sin(wt – 85,45º) + 22,24
= 4,94sin(wt – 85,45º) + 22,24 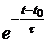 – Imsinj
– Imsinj 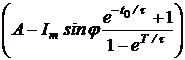
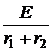 =
= 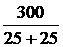 = 6 A,
= 6 A,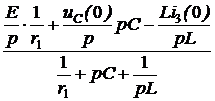 =
= 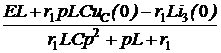 =
= 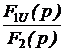 ;
;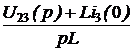 =
= 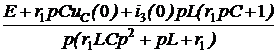 =
= 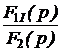 .
.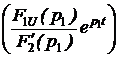 ;
;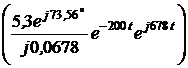 = 156,3e -200tcos(678t – 16,44°) =
= 156,3e -200tcos(678t – 16,44°) =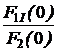 + 2Re
+ 2Re 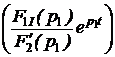 ;
;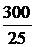 + 2Re
+ 2Re 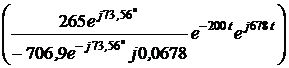 =
=
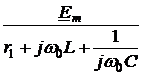 =
= 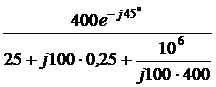 = 16·e –j45° А;
= 16·e –j45° А;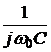 = 16·e –j45°·(-j25) = 400·e –j135° B;
= 16·e –j45°·(-j25) = 400·e –j135° B;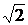 A, uC(0+) = uC(0-) =400sin(-135°) = -200
A, uC(0+) = uC(0-) =400sin(-135°) = -200 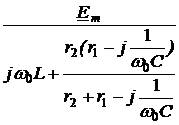 =
= 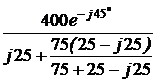 = 16·e –j73,05° А;
= 16·e –j73,05° А;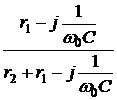 = 16·e –j73,05°·
= 16·e –j73,05°· 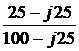 = 5,49·e –j104° А;
= 5,49·e –j104° А;