
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задание нагрузок и закрепленийС математической точки зрения и нагрузки, и закрепления представляют собой граничные условия, наложенные на обобщенные перемещения узлов конечно-элементной модели исследуемого тела. При решении механической задачи единые граничные условия удобно разделять на закрепления (constraints) и нагрузки (loads). В универсальных пакетах для одной модели может быть несколько наборов произвольных (в том числе разнотипных) закреплений и нагрузок. При желании их можно комбинировать произвольным образом. Закрепления представляют собой запрет на перемещение выбранного узла в том или ином направлении. Любой узел, в принципе, может перемещаться вдоль осей координат X, Y, Z или вращаться вокруг этих осей. Иными словами, он имеет шесть степеней свободы (degrees of freedom, DOF). Для решения механической задачи методом конечных элементов заключается в том, что исследуемое тело должно быть зафиксировано. Для этого достаточно указать на выбранные узлы конечно-элементной сетки и ограничить их степени свободы. Иногда бывает удобно ограничить степени свободы узла, задав его координаты в цилиндрической (cylindrical) или сферической (spherical) системах координат. Например, так удобно задавать закрепление вала в радиальном подшипнике, когда необходимо запретить перемещение вдоль радиуса, но оставить возможным вращение вала и возможность его перемещение в осевом направлении. Для механических задач нагрузка задается как сила (force) или пара сил (moment), перемещение (displacement) или угол поворота (enforced rotation) и, в некоторых специфических случаях, линейную (velocity) или угловую (rotational velocity) скорость и ускорение (acceleration, rotational acceleration). Нагрузки прикладываются к какому-то узлу (или узлам). Обычно для задания параметров нагрузки необходимо вызвать команду задание нагрузки (load) и выбрать необходимые узлы. Далее, в появившемся меню, следует выбрать значения составляющих нагрузки.  Распределенными нагрузками может быть, например, давление (pressure) или погонная сил (сила на единицу длины, force per length). Интересным видом распределенных нагрузок являются объемные нагрузки, вызванные весом тела или центробежной силой при вращении. Они прикладываемые ко всем конечным элементам, аппроксимирующим тело. После задания любого вида распределенных нагрузок машина автоматически рассчитывает силу, приходящуюся на один узел выбранного участка конечно-элементной сетки, с учетом размера и формы конечных элементов. К тепловым нагрузкам относится температура (temperature), тепловыделение (мощность генерации тепла на единицу объема тела, heat generation), тепловой поток (тепловая энергия, переносимая через единицу площади, heat flux). В свою очередь, одним из источников теплового потока могут быть конвективный поток (convection) и радиационное излучение (radiation). Обязательным условием при проведении любого вида теплового расчета служит задание начальной температуры тела (начальное условие). Например, при конвективным теплообмене жидкости или газы, находящиеся в контакте с твердым телом, либо отдают ему тепло (нагревают), либо получает от него тепло (охлаждают). Количество теплоты Q, Вт, проходящее через поверхность раздела площадью S, м2, определяется зависимостью:
где a – коэффициент теплоотдачи, [a]=Вт/м2´оС; Ттело – температура твердого тела, оС; ТО.С. – температура окружающей среды (жидкости или газа), оС. Также как и для закреплений, при задании нагрузок возможно использование не только прямоугольной (rectangular), но также цилиндрической (cylindrical) или сферической (spherical) систем координат. Это может быть удобным, например, при задании контактных сил в сопряжении «вал – втулка». В нагрузку могут быть преобразованы и результаты предыдущего расчета, не обязательно того же вида. Например, стандартным способом задания остаточных механических напряжений в теле служат результаты теплового расчета. Виды конечно-элементных расчетов. Статические расчеты Расчеты, в том числе и конечно-элементные, можно разделить на статические и динамические. В свою очередь, оба эти вида расчетов могут быть линейные и нелинейные. При статических расчетах предполагается, что внешняя нагрузка и параметры материала не зависят от времени. При динамических расчетах либо нагрузка, либо свойства материала меняются во времени. В случае линейной модели исследуемой системы результат решения прямо пропорционален величине внешнего воздействия. Например, прогиб балки линейно зависит от величины приложенной силы. В инженерной практике наиболее часто используется статический линейный расчет. Но для наиболее точного отражения поведения реального объекта необходимо использовать нелинейные и, желательно, динамические расчеты. Для механических систем выделяют три основных вида нелинейности: 1) геометрическая нелинейность, вызванная тем, что перемещения элементов механической системы под нагрузкой становятся сравнимы с размерами самой системы; 2) физическая нелинейность, вызванная зависимостью свойств материала от истории нагружения; |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 782. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
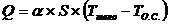 ,
,