
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Оцінка впливу випадкових похибок обмеженої кількості прямих спостережень.Усе наведене раніше, в тому числі щодо обчислення довірчого інтервалу, справедливе лише при наявності достатнього об`єму інформації, одержаної від великого числа спостережень, тобто коли n→∞. Звичайно ж на практиці кількість спостережень у кожному ряду обмежена, що значно зменшує достовірність наявної інформації. Тож чи можна при цьому користуватись обчисленим довірчим інтервалом? Відомий англійський математик Госсет (псевдонім Ст`юдент) дав ствердну відповідь. Але при цьому довірчий інтервал повинен бути розширений множенням його на коефіцієнт t (n, P), названий згодом коефіцієнтом Ст`юдента. Цей коефіцієнт залежить, перш за все, від кількості спостережень, тобто від об`єму інформації. При дуже великій кількості спостережень, коли n→∞ , t (n, P) → 1. При зменшенні кількості спостережень коефіціент Ст`юдента зростає (табл. 5.).
Значення коефіцієнта Ст`юдента для довірчих імовірностей P = 0,95; 0,99; 0,999 при різній кількості вимірювань, n, наведені в табл. 5 [6]. Таким чином, з урахуванням коефіцієнта Ст`юдента напівш-ирина довірчого інтервалу:
Найпоширеніша послідовність дій при опрацюванні правильних результатів вимірювань (що не містять систематичних похибок) прямих рівноточних спостережень наступна.  1. Після виконання n спостережень маємо результати:
x1, x2, x3, ..., xn
2. Знаходимо середнє арифметичне значення
3. Обчислюємо ‘’n ‘’залишкових похибок:
nI = Xi -
4. Вираховуємо за формулою Бесселя СКВ σ:
5. Задаємось довірчою імовірністю Р. При технічних вимірюваннях цілком досить Р = 0,95. При дуже відповідальних вимірюваннях, пов`язаних із безпекою польотів, розподілом матеріальних цінностей і т. ін., задаються вищими значеннями довірчої імовірності Р, в залежності від відповідальності вимірювань. Знаючи кількість спостережень n та довірчу імовірність Р, можна знайти за табл. 5 коефіцієнт Ст`юдента. 6. Обчислюємо напівширину довірчого інтервалу 7. Записуємо результат вимірювання у стандартизованій формі, що містить три числа: -середньоарифметичне значення виміряної величини; -довірчий інтервал; -довірчу імовірність, тобто:
Наприклад, одержали результат вимірювання напруги:
U = 100 В ± 3 В; P= 0,95.
Це значить, що після багаторазових спостережень виявили, що найбільш достовірним значенням напруги є 100 В. Причому, принаймні, в 95 спостереженнях із 100 результат має значення не менше за 97 В (тобто 100 В – 3 В) і не більше за 103 В (тобто 100 В + 3 В). Допускається, якщо похибки вимірювань розподіляються за нормальним законом, довірча імовірність Р = 0,95, а довірчий інтервал симетричний, використовувати скорочений запис результату вимірювань, не вказуючи довірчу імовірність, а саме:
Наприклад: U = (100 ± 3) В. Запитання для самоперевірки: 1. Чи можна дослідним шляхом уникнути випадкових похибок у результатах вимірювань? Чому? 2. Яким критерієм характеризують та порівнюють між собою точність різних рядів спостережень? 3. Як виглядає та яким аксіомам відповідає закон розподілу випадкових похибок? 4. Як обчислити за формулою Бесселя СКВ? 5. Як обчислити СКВ середніх арифметичних значень багатьох рядів спостережень? Що потрібно зробити для зменшення впливу випадкових похибок на результати багаторазових спостережень, наприклад, у 10 разів? 6. Які апроксимації законів розподілу випадкових похибок вам відомі? Які приклади практичної реалізації цих апроксимацій ви можете навести? 7. Що таке гістограма та як її побудувати ? 8. Що таке коефіцієнт Ст`юдента? Від чого він залежить? Де його брати? 9. Що таке довірчий інтервал і довірча імовірність та як вони пов`язані з коефіцієнтом Ст`юдента? 10.Який алгоритм опрацювання результатів обмеженої кількості спостережень вам відомий? У якій формі слід подавати результати вимірювань? 9. ВИВЧЕННЯ ПОХИБКИ РЕЗУЛЬТАТУ ОПОСЕРЕДКОВАНОГО ВИМІРЮВАННЯ Результат опосередкованого вимірювання визначається після виконання математичних операцій над даними, отриманими прямими вимірюваннями:
де уце результат опосередкованого вимірювання; fце відома функція;
це результати прямих вимірювань. Якщо відомі абсолютні похибки усіх прямих вимірювань,
де: Наприклад, визначаємо потужність Р електричного струму, вимірявши його силу I з похибкою
Потужність
Параметри точності результатів прямих вимірювань окре-мих величин Тож, нехай, як і раніше, виконали опосередковане вимірювання:
Відомі результати прямих вимірювань його складових:
СКЛАДАННЯ ПОХИБОК
Досі, аналізуючи похибки вимірювань ,ми розкладали їх на окремі складові частини. Одні з них визначались недосконалістю методу вимірювання, другі вносились за рахунок недосконалості використаних ЗВТ, їх впливу на об'єкт, за рахунок зміни впливних параметрів довкілля і т.ін. Тепер поставимо задачу складання всіх цих частин для визначення загальної похибки вимірювання. Нехай відомі "n" складових частин похибки, які виникають із різних причин та не пов'язані між собою (їх кореляція дорівнює нулеві). Вважатимемо також, що ці складові частини мають нормальний закон розподілу кожна, що найчастіше зустрічається на практиці. Якщо довірчі інтервали складових частин похибки обрати за правилом "трьох сігм", тобто Можливі два способи визначення загальної похибки: арифметичне та геометричне складання окремих частин похибки. Арифметичне складання. У цьому випадку загальна похибка
де
Як видно з формули, в результаті обчислень одержимо найбільшу з можливих на практиці похибок. Вона може бути лише тоді, коли всі складові похибки мають найбільше з можливих значень та одночасно діють із однаковим знаком. Імовірність такого збігу обставин дуже мала. Якщо у відомій байці лебідь, рак та щука не можуть одночасно тягнути воза з найбільшою силою та ще й в одному напрямку, то, тим паче, не можуть усі складові похибки мати одночасно однаковий знак та найбільший розмір. Тому, як правило, експериментально визначена похибка значно менша від визначеної за формулою арифметичного складання. Так обчислювати похибку слід лише у надзвичайно відповідальних випадках, пов’язаних із небезпекою для життя, можливістю катастроф і т.ін. У повсякденній інженерній практиці, а також у розрахун-ках ваших курсових та дипломних проектів використовувати цю формулу не рекомендується, тому що вона дає дуже погані, а гол-овне, і малореальні параметри точності. Геометричне складання. Цей метод грунтується на центральній теоремі теорії імовірностей, і для обчислення загальної похибки пропонує формулу:
Використання цієї формули дає значно кращі результати. загальна похибка виходить значно меншою, ніж у попередньому випадку, що, як правило, ближче до бажаних значень параметрів точності проектованих виробів. Але наскільки обґрунтованим та чесним для вимогливого до себе інженера є використання цієї формули замість попередньої? Розрахунки з використанням математичного апарату теорії імовір-ностей показують, що довірча імовірність довірчого інтервалу, об-численого за цією формулою, р=0.9973. Це дуже висока імовірність, яка показує, що не більш як у 0,27 % випадків експериментально ви-значена похибка може перевищити похибку-обчислену за форму-лою геометричного складання.
Запитання для самоперевірки.
1. Як обчислити похибку результату опосередкованого вимірювання, коли похибки результатів його складових подані в інтервальній формі? 2. Яким чином від подання параметрів точності спостережень у формі СКВ перейти до інтервальної форми? 3. Як обчислити похибку результату опосередкованого вимірювання, коли похибки результатів його складових подані у формі СКВ? 4. Яким чином виконується та коли застосовується арифметичне складання похибок? 5. Яким чином виконується та коли застосовується геометричне складання похибок? МЕТРОЛОГІЧНЕ ЗАБЕЗПЕЧЕННЯ |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 466. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Коефіцієнт Ст`юдента також залежить від обраної довірчої імовірності, тобто від претензій на достовірність (див.табл.5). При помірних претензіях на достовірність (P = 0,95) коефіцієнт t (n, P) невеликий. В той же час при надмірних претензіях на достовірність (наприклад, при P = 0,999, коли дозволяється не більш як одному значенню похибки з ряду в 1000 спостережень вийти за обчислений довірчий інтервал) коефіцієнт Ст`юдента різко зростає.
Коефіцієнт Ст`юдента також залежить від обраної довірчої імовірності, тобто від претензій на достовірність (див.табл.5). При помірних претензіях на достовірність (P = 0,95) коефіцієнт t (n, P) невеликий. В той же час при надмірних претензіях на достовірність (наприклад, при P = 0,999, коли дозволяється не більш як одному значенню похибки з ряду в 1000 спостережень вийти за обчислений довірчий інтервал) коефіцієнт Ст`юдента різко зростає.
 :
:
 ,
,
 :
:




 , то можна знайти абсолютну похибку результату опосередкованого вимірювання
, то можна знайти абсолютну похибку результату опосередкованого вимірювання  за формулою:
за формулою:
 це частинні похідні функції непрямого вимірювання за кожним із аргументів.
це частинні похідні функції непрямого вимірювання за кожним із аргументів. I та знаючи опір об'єкта R із похибкою
I та знаючи опір об'єкта R із похибкою  .
. тобто:
тобто: 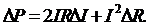
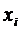 можуть бути подані не у вигляді їх абсолютних по-хибок
можуть бути подані не у вигляді їх абсолютних по-хибок  , тобто у так званій інтервальній формі, а через СКВ ,σxi. Це більш інформативна форма подання параметрів точності вимі-рювання.Зв'язок між інтервальною та за допомогою СКВ формами подання параметрів точності вимірювання визначається законом розподілу похибок. Для нормального закону розподілу похибок довірчій імовірності Р=0,95 відповідає довірчий інтервал
, тобто у так званій інтервальній формі, а через СКВ ,σxi. Це більш інформативна форма подання параметрів точності вимі-рювання.Зв'язок між інтервальною та за допомогою СКВ формами подання параметрів точності вимірювання визначається законом розподілу похибок. Для нормального закону розподілу похибок довірчій імовірності Р=0,95 відповідає довірчий інтервал  , а при довірчій імовірностіР=0,997;
, а при довірчій імовірностіР=0,997;  .
.
 та їх СКВ:
та їх СКВ:  Тоді СКВ результату опосередкованого вимірювання
Тоді СКВ результату опосередкованого вимірювання
 , це практично визначає найбільші можливі їх значення. При цьому, довірча імовірність Р=0,9973 означає, що при 10 000 вимірювань не більш за 27 похибок можуть вийти за межі
, це практично визначає найбільші можливі їх значення. При цьому, довірча імовірність Р=0,9973 означає, що при 10 000 вимірювань не більш за 27 похибок можуть вийти за межі 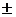
 .
.
 - абсолютне значення найбільшого можливого розміру і-ї складової частини похибки.
- абсолютне значення найбільшого можливого розміру і-ї складової частини похибки.