Вращение точки, отрезка прямой, плоскости вокруг оси,

ПЕРПЕНДИКУЛЯРНОЙ К ПЛОСКОСТИ ПРОЕКЦИЙ

Вращение вокруг заданной оси.

1. Пусть точка А вращается вокруг оси, перпендикулярной к плоскости. 1

Через точку А проведена плоскость., перпендикулярная к оси вращения и,

следовательно, параллельная пл. 1. При вращении точка А описывает в пл.

окружность радиуса R; величина радиуса выражается длиной перпендикуляра,

проведенного из точки А на ось. Окружность, описанная в пространстве точкой

А, проецируется на пл. 1 без искажения. Так как пл. перпендикулярна к

пл. 2, то проекции точек окружности на пл. 2 расположатся на ", т. е. на

прямой, перпендикулярной к фронтальной проекции оси вращения. Чертеж дан на

рис. 212 справа: окружность, описанная точкой А при вращении ее вокруг оси,

спроецирована без искажения на пл. 1 Из точки О', как из центра, проведена

окружность радиуса R; на пл. 2 эта окружность изображена

отрезком прямой, равным 2R.

17.Натуральную величину плоского геометрического образа можно определить вращением его вокруг горизонтали или фронтали до положения, параллельного одной из плоскостей проекций.

На рис. 90 показано вращение некоторой точки A вокруг горизонтальной прямой NM до тех пор, пока точка A не окажется в плоскости, параллельной плоскости проекций П₁ и определяемой этой точкой и осью вращения. При вращении вокруг горизонтальной прямой MN точка Aперемещается по дуге радиуса OA, лежащей в плоскости Q, перпендикулярной к оси вращения. Когда точка A займет нужное положение A¹, горизонтальная проекция радиуса вращения (O₁A₁¹) будет равна его истинной величине, которая может быть определена способом прямоугольного треугольника.

На рис. 91 эти же построения выполнены на эпюре.

На рис. 92 показано нахождение истинной величины треугольника ABC вращением его вокруг горизонтали A1.

18. Построение проекции многогранника на нек.оторой плоскости сводится к построению проекций точек. Например, проецируя пирамиду SABC на пл.π₂ (рис. 256, слева), мы строим проекции вершин S, А, В и С и, как следствие, проекции основания АВС, граней SAB, SBC, SAC, ребер SA, SB и др.

Также, проецируя трехгранный угол ¹) с вершиной S (рис. 256, справа), мы, помимо вершины S, берем на ребрах угла по одной точке (К, М, N) и проецируем их

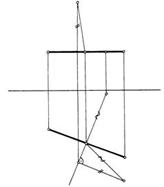
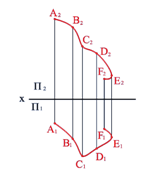
на пл. π₂; в результате получаем проекции ребер и граней (плоских углов) трехгранного угла и в целом самый угол.

· Чертежи призм и пирамид

Положим, что нам известна по форме и положению фигура, полученная при пересечении всех боковых граней призмы плоскостью, и известно направление ребер призмы (рис. 258). Этим задается призматическая поверхность. Пересекая призматическую поверхность двумя параллельными между собой плоскостями, мы получаем основания призмы (рис. 258). Можно задаться одним из оснований призмы и ее высотой или длиной бокового ребра и тем задать призму.

Выбирая положение призмы для ее изображения, целесообразно располагать ее основания параллельно плоскости проекций.

Какие признаки позволяют установить, что на данном чертеже изображена именно призма (или, в частности, параллелепипед)? Наличие на чертеже только прямолинейных отрезков ²), причем они служат проекциями или ребер, или граней, наличие параллелограммов или прямоугольников как проекций боковых граней и любого многоугольника как проекции основания.

· 19.Пересечение призм и пирамид плоскостью и прямой линией

Для построения фигуры, получаемой при пересечении призмы и пирамиды плоскостью, надо или найти точки, в которых ребра призмы или пирамиды пересекают данную плоскость, или найти отрезки прямых, по которым грани призмы или пирамиды пересекаются плоскостью. В первом случае построение сводится к задаче на пересечение прямой с плоскостью, во втором случае — на пересечение плоскостей между собой.

В тех случаях, когда секущая плоскость не параллельна ни одной из плоскостей проекций, фигура сечения проецируется с искажением. Поэтому, если требуется определить натуральный вид фигуры сечения ¹), то следует применять один из способов, которые позволяют находить длину отрезка, величину угла и т. д.При пересечении получается четырехугольник, вершины которого представляют собой точки пересечения ребер призмы с пл.δ.Так как в данном случае призма прямая и основание ее параллельно пл. π₁, то горизонтальная проекция фигуры сечения определяется сразу, без какого-либо построения: она накладывается на проекцию A'B'C'D

· 20. Пересечение одной многогранной поверхности другою

Построение линии взаимного пересечения многогранных поверхностей можно производить двумя способами, комбинируя их между собой или выбирая из них тот, который в зависимости от условий задания дает более простые построения. Эти способы следующие:

1)Определяют точки, в которых ребра одной из поверхностей пересекают грани другой и ребра второй пересекают грани первой ¹). Через найденные точки в определенной последовательности проводят ломаную линию, представляющую собой линию пересечения данных поверхностей. При этом можно соединять прямыми проекции лишь тех точек, полученных в процессе построения, которые лежат в одной и той же грани.

2)Определяют отрезки прямых, по которым грани одной поверхности пересекают грани другой ²); эти отрезки являются звеньями ломаной линии, получаемой при пересечении многогранных поверхностей между собой.

¹) Задача на пересечение прямой линии с плоскостью.

²) Задача на пересечение двух плоскостей между собой.

Если проекция ребра одной из поверхностей не пересекает проекции грани другой хотя бы на одной из проекций, то данное ребро не пересекает этой, грани. Однако пересечение проекций ребра и грани еще не означает, что эти ребро и грань пересекаются в пространстве.

В некоторых из приводимых ниже примеров применены изложенные выше общие схемы построения точек пересечения, в других — использованы частные особенности для упрощения построений.

21. Под разверткой многогранной поверхности подразумевают плоскую фигуру, составленную из граней этой поверхности, совмещенных с одной плоскостью.

Существуют три способа построения развертки многогранных поверхностей:

1) способ нормального сечения;

* Геометрическое преобразование, при котором сохраняются величины углов, называется конфорным, следовательно, построение разверток является конфорным преобразованием, а поверхность и ее развертка конфорны.

** Геодезической называется линия, принадлежащая поверхности и соединяющая кратчайшим путем две точки, также принадлежащие поверхности.

2) способ раскатки;

3) способ треугольников (триангуляции).

Первые два применяются для построения развертки призматических поверхностей, третий - для пирамидальных поверхностей. Рассмотрим каждый их этих способов.

22. Кривая линия в ряде случаев представляет собой геометрическое место точек, отвечающих определенным для этой кривой условиям (окружность, эллипс, парабола и т. п.).

Кривая линия определяется положениями составляющих ее точек. Точки кривой определяются их координатами.

Кривые линии могут быть плоские, т. е. такие, которые всеми своими точками лежат в одной плоскости, и пространственные, т. е. такие, точки которых не принадлежат одной плоскости³). Примерами плоскйх кривых линий являются окружность, эллипс, парабола, спираль Архимеда; примерами пространственных кривых — винтовая линия, линия пересечения боковых поверхностей прямых круговых цилиндра и конуса.

Для построения проекций кривой (плоской или пространственной) необходимо построить проекции ряда принадлежащих ей точек (рис. 289). Пример построения проекций плоской кривой по точкам был дан на рис. 119 (с. 48).

Пространственная кривая проецируется в виде плоской, плоская кривая — также в виде плоской или в виде прямой линии, если кривая находится в плоскости, перпендикулярной к плоскости проекций.

Линия считается закономерной, если в своем образовании она подчинена какому-либо геометрическому закону. Если при этом кривая определяется в декартовых координатах алгебраическим уравнением, то она называется алгебраической ⁴). Примером может служить эллипс, его уравнение x²/a² + y²/b² = 1. Степень уравнения определяет «порядок» кривой: эллипс — кривая второго порядка. Кривая, представляющая собой проекцию кривой некоторого порядка, сохраняет тот же порядок или оказывается кривой более низкого порядка.

Касательная к кривой проецируется в общем случае в виде касательной кпроекции этой кривой. Если, например, к окружности, расположенной в плоскости, составляющей с плоскостью проекций острый угол, проведена касательная, то

¹) Траектория — от trajectio (лат.) — передвижение, перемещение.

²) На протяжении кривой линии не должно быть прямолинейных участков.

³) Пространственные кривые называют также линиями двоякой кривизны.

ространственные кривые линии в начертательной геометрии обычно рассматриваются как результат пересечения поверхностей или траектория движения точки.

Пространственную, так же как и плоскую, кривую линию на чертеже задают последовательным рядом точек.

Классическим примером пространственных кривых линий являются цилиндрическая и коническая винтовые линии

· 23. Общие сведения о кривых поверхностях

1. Поверхность можно представить себе как общую часть двух смежных областей пространства.. Представление о поверхности как о совокупности всех последовательных положений некоторой перемещающейся в пространстве линии удобно для графических построений ¹

Линию, производящую поверхность, в каждом ее положении называют образующей (или производящей). Образующая обычно указывается в ряде ее положений.

2. Поверхность, которая может быть образована, прямой линией, называется линейчатой поверхностью. Линейчатая поверхность представляет собой геометрическое место прямых линий. Поверхность, для которой только кривая линия может быть образующей, будем называть нелинейчатой поверхностью ³).

· Поверхности вращения

В числе кривых поверхностей — линейчатых и нелинейчатых — имеются широко распространенные в практике поверхности вращения. Поверхностью вращения называют поверхность, получаемую от вращения какой-либо образующей линии вокруг неподвижной прямой — оси поверхности ¹).

Поверхность вращения можно задать образующей и положением оси. На рис. 330 показана такая поверхность. Здесь образующей служит кривая ABC, осью — прямая OO₁, расположенная в одной плоскости с ABC. Каждая точка образующей описывает окружность. Таким образом, плоскость, перпендикулярная к оси поверхности вращения, пересекает эту поверхность по окружности.

На рис. 337 изображен один виток винтовой поверхности, образованной движением отрезка АВ. Прямая, определяемая данным отрезком, во всех положениях пересекает ось под одним и тем же углом (на рис. 337 угол 60°). Перемещение концов отрезка вдоль оси пропорционально угловому перемещению отрезка.

Точки А и В образуют цилиндрические винтовые линии, как и все точки отрезка АВ, и, следовательно, для более точного изображения очерка винтовой поверхности на пл. π₂надо было бы провести возможно больше проекций винтовых линий, описываемых различными точками отрезка АВ, и затем провести кривые, огибающие эти проекции. Практически вместо этого громоздкого построения обычно проводят прямые, одновременно касающиеся проекций винтовых линий (см. рис. 345). Если наклон образующей по отношению к оси цилиндра не равен 90° (например, 60° на рис. 337), то винтовая поверхность носит название косой. Если же этот угол равен 90°, то образуется прямая винтовая поверхность

24. Пересечение прямой с поверхностью Для того чтобы найти точки пересечения прямой с поверхностью любого тела (цилиндр, конус, шар и т. д.), поступают точно также, как и при нахождении точки пересечения прямой с плоскостью, а именно:

заданную прямую заключают во вспомогательную плоскость;

находят линию (кривую) пересечения заданной поверхности со вспомогательной плоскостью;

на пересечении заданной прямой с линией пересечения получают искомые точки .

найти линию пересечения этой плоскости с поверхностью; точка пересечения заданной прямой и построенной линии на поверхности и будет искомой точкой пересечения прямой с поверхностью.

25. Пересечение плоскостью поверхности вращения

Линия пересечения кривой поверхности плоскостью представляет собой плоскую кривую линию (сечение), для построения которой необходимо определить отдельные точки сечения и соединить и последовательно плавной кривой.

Построение точек сечения поверхности вращения, как правило, начинают с определения опорных точек. К ним относятся следующие точки: высшая и низшая, ближайшая и наиболее удаленная, точки видимости и др.

· Остальные точки (промежуточные) находятся либо по линиям связи, т.е. без дополнительных построений, либо с применением вспомогательных секущих плоскостей.Проецирование линии пересечения двух поверхностей вращения второго порядка на плоскость, параллельную их общей плоскости симметрии

В ряде случаев имеет место пересечение одной поверхности вращения второго порядка другою. При этом, как и для всех алгебраических поверхностей второго порядка, получается пространственная кривая четвертого порядка, называемая биквадратной.

В сноске на с. 208 было сказано, что если две. поверхности второго порядка имеют общую для них плоскость симметрии, то получаемая кривая пересечения этих поверхностей проецируется на плоскость, параллельную их плоскости симметрии, в виде кривой второго порядка. На рис. 412, к которому относилась эта сноска, были представлены два конуса вращения с пересекающимися осями, определявшими общую для этих конусов плоскость симметрии, параллельную пл. π₂. Фронтальная проекция полученной при этом биквадратной кривой представляла собой гиперболу.

26. Для определения линии пересечения двух произвольных поверхностей вращения целесообразно воспользоваться одним свойством, присущим поверхностям вращения, которое состоит в том, что две любые соосные поверхности вращения пересекаются по окружностям, проходящим через точки пересечения меридианов поверхностей.

В частном случае, если одна из поверхностей вращения – сфера, приведенное выше предложение может быть сформулировано иначе: если центр секущей сферы находится на оси поверхности вращения, то сфера пересечет данную поверхность по окружностям, число которых равно числу точек пересечения главных меридианов поверхностей.

Построить линии пересечения поверхностей с помощью вспомогательных секущих сфер можно двумя способами:

1. Способом концентрических сфер;

2. Способом эксцентрических сфер.