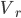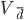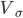Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Среднее квадратическое отклонениеНаиболее совершенной характеристикой вариации является среднее квадратическоеоткложение, которое называют стандартом (или стандартным отклонение).Среднее квадратическое отклонение ( Среднее квадратическое отклонение простое:
Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности. Дисперсия Дисперсия простая:
Более удобно вычислять дисперсию по формуле:
которая получается из основной путем несложных преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней. Для несгрупиированных данных:
Для сгруппированных данных:
Вариация альтернативного признака заключается в наличии или отсутствии изучаемого свойства у единиц совокупности. Количественно вариация альтернативного признака выражается двумя значениями: наличие у единицы изучаемого свойства обозначается единицей (1), а его отсутствие — нулем (0). Долю единиц, обладающих изучаемым признаком, обозначают буквой 
средний квадрат отклонений
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным свойством ( Относительные показатели вариации включают: § Коэффициент осцилляции § Относительное линейное отклонение (линейный коэффициент варианции) § Коэффициент вариации (относительное отклонение) |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 417. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
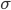 ) равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:
) равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической: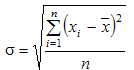
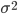 - представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.
- представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.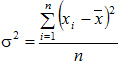

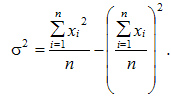
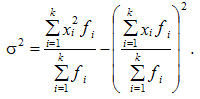
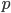 , а долю единиц, не обладающих этим признаком — через
, а долю единиц, не обладающих этим признаком — через 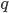 . Учитывая, что p + q = 1 (отсюда q = 1 — p), а среднее значение альтернативного признака равно
. Учитывая, что p + q = 1 (отсюда q = 1 — p), а среднее значение альтернативного признака равно 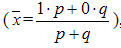 ,
,