
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Геометрический метод решения системы линейных неравенств с двумя переменнымиСовокупность линейных неравенств с общими неизвестными называется системой линейных неравенств.
Неравенства могут быть одного смысла (≤ или ≥) или разного. Множество решений, которое удовлетворяет каждому неравенству системы, называется решением системы неравенств. Системы неравенств, имеющие хотя бы одно решение, называются совместными. Если системы неравенств не имеют решений, то они – несовместные. Если система m неравенств с двумя переменными совместна, то множеством решений такой системы является выпуклый многоугольник или выпуклая многоугольная область (неограниченная). Множеством решений системы линейных неравенств с двумя переменными может быть: 1) Точка; 2) Пустое множество; 3) Выпуклый многоугольник; 4) Выпуклая неограниченная область. Пример: Построить область решений системы линейных неравенств:
1)
x1 = 0; x2 = 5 x2 = 0; x1 = -10/5 О(0;0) ≤ 10 – верно 2)
x1 = 0; x2 = 6,2 x2 = 0; x1 = 14 О(0;0) ≤ 56 – верно 3)
x1 = 0; x2 = 4/3
О(0;0) ≥ 4 – неверно
Точки пересечения:
10х2 = 86 х2 = 8,6 -3х1 = 7,2 х1 = 2,4 (2,4; 8,6)
Прямая линия на плоскости.
1.1. Уравнение линии на плоскости.
Положение точки на плоскости определяется двумя координатами. Прямоугольная декартова система координат на плоскости представляет из себя две перпендикулярные прямые, снабженные масштабами и направлениями. Такие прямые называются координатными осями - осью абсцисс Ох и осью ординат Оy. Пусть на плоскости заданы декартова прямоугольная система координат и некоторая линия L. Рассмотрим уравнение F(x,y)=0 (или y=j(x)), связывающее две переменные величины x и y. Это уравнение называется уравнением линии L (относительно заданной системы координат), если 1) ему удовлетворяют координаты (x,y) любой точки линии L и 2) ему не удовлетворяют координаты ни одной точки, не лежащей на линии L.  1.2. Различные виды уравнения прямой.
В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени Ax + By + C = 0 (1) (где А и В не равны нулю одновременно) определяет некоторую прямую. Это уравнение называется общим уравнением прямой. Возможны следующие случаи: 1) С = 0, уравнение имеет вид Ax + By = 0 и определяет прямую, проходящую через начало координат; 2) В = 0 (А ¹ 0), уравнение принимает вид Ax + C = 0 или x = 3) А = 0 (В ¹ 0), уравнение принимает вид Вy + C = 0 или y =
  Замечание. Для построения прямой, заданной общим уравнением, достаточно указать любые две ее точки. Замечание. Для построения прямой, заданной общим уравнением, достаточно указать любые две ее точки.
  Пример 1. Определить точки пересечения прямой 3x - 4y + 12= 0 с координатными осями и построить эту прямую. Пример 1. Определить точки пересечения прямой 3x - 4y + 12= 0 с координатными осями и построить эту прямую.
 Решение. Полагая x = 0, находим y = 3; таким образом, получена точка М(0,3) пересечения Решение. Полагая x = 0, находим y = 3; таким образом, получена точка М(0,3) пересечения
прямой с осью Oy. При y = 0 значение x = -4 и N(-4,0) - точка пересечения прямой с осью Ox. Осталось провести прямую через точки М и N (рис. 1). ■ Если ни один из коэффициентов уравнения (1) не равен нулю, то его можно преобразовать к виду
где a = Рассмотрим на плоскости xOy прямую, не параллельную оси Oy; при движении вдоль такой прямой в одном направлении x возрастает, а в другом убывает. Направление, отвечающее возрастанию x, назовем положительным. Угол a, на который надо повернуть положительную полуось Оx, чтобы совместить ее с положительным направлением данной прямой, называют углом наклона прямой к оси абсцисс. При этом угол наклона считается положительным, если положительную полуось Оx надо поворачивать против часовой стрелки, и отрицательным в противном случае, так что Угловым коэффициентом прямой k называется тангенс угла наклона прямой к оси Оx: k = Замечание. Прямая, параллельная оси Оy, не имеет углового коэффициента, т.к. Если прямая не параллельна оси Оy, то ее уравнение можно записать в виде y = kx+b. (3) Это уравнение называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент; b - величина отрезка, который отсекает прямая на оси Оy, считая от начала координат. В частном случае, при b = 0 прямая y = kx проходит через начало координат. Из общего уравнения прямой (1) при В¹0 можно получить уравнение y = Пример 2. Найти угол наклона к оси Оx прямой, заданной общим уравнением 2x + 5y + 17= 0. Решение. Выразим из данного уравнения y. Получим уравнение прямой с угловым коэффициентом y = Рассмотрим далее решение некоторых типовых задач. |
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 237. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 – прямая l1
– прямая l1
 – прямая l2
– прямая l2
 – прямая l3
– прямая l3 x2 = 0; x1 = 0,8
x2 = 0; x1 = 0,8
 - прямая, параллельная оси Oy (в частности, x = 0 - уравнение самой оси Oy);
- прямая, параллельная оси Oy (в частности, x = 0 - уравнение самой оси Oy); - прямая, параллельная оси Ox (в частности, y = 0 - уравнение самой оси Ox).
- прямая, параллельная оси Ox (в частности, y = 0 - уравнение самой оси Ox). , (2)
, (2) , легко определить координаты точек М и N.
, легко определить координаты точек М и N. < a <
< a <  . Можно считать, что для прямой, параллельной оси Оy, угол наклона a =
. Можно считать, что для прямой, параллельной оси Оy, угол наклона a =  .
. не существует; или можно считать, что ее угловой коэффициент равен бесконечности, т.к. при a ®
не существует; или можно считать, что ее угловой коэффициент равен бесконечности, т.к. при a ® 
 .
.
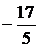 . Откуда, k =
. Откуда, k =  = -0,4, так что
= -0,4, так что  . ■
. ■