Элементы повышения быстродействия системы

Анализ эффективности коалиционного алгоритма перехвата на основе векторного равновесия показал, что время расчета ПКЗУ превышает время взаимодействия, поэтому необходимо увеличение быстродействия системы с целью приблизить такт выдачи управлений к реальному.

При дополнительном изучении поставленной задачи и разработанного алгоритма было выявлено несколько наиболее значимых, с точки зрения быстродействия, путей ускорения данного метода оптимизации управления в рамках рассмотренного примера.

3.5.1. Получение аналитического решения системы (3.50)

Одной из наиболее трудоемких и многократно циклически-повторяемых в данном алгоритме является процедура моделирования (численного интегрирования системы (3.50) 5-го порядка методом Рунге–Кутта). Используя современные программные продукты (пакет символьных вычислений и преобразований MAPLE 5.04) удалось найти аналитическое решение данной системы (см. выше) в виде суммы ряда:

где a_i, b_i, c_i, d_i, g_i – сложные выражения специального вида.

3.5.2. Выбор области начальных приближений
на основе минимаксного подхода

Во многих задачах группового противодействия часто бывает возможным выделить главные объекты коалиций (лидеры). Остальные объекты коалиций выбирают свои параметры управления уже с учетом выбранных управлений главным объектом. Такая ситуация имеет место и в примере, где в качестве лидеров выступают цель и один из перехватчиков (ведущий). Взаимодействие «ведущий–ведомый» внутри звена легко учесть, введя понятие «конуса доминирования» для коалиции истребителей-перехватчиков. При малых l для ведущего и цели можно рассмотреть ситуацию  где .

Такое чисто антагонистическое противодействие может рассматриваться с позиции минимаксного подхода.

Были построены области значений показателя для ведущего (рис. 3.14) и для цели (рис. 3.15). Каждое вертикальное сечение областей представляет собой область достижимости показателей ведущего (рис. 3.14) или цели (рис. 3.15), полученную на диапазоне изменений собственных параметров при фиксированных параметрах «партнера». Поэтому на рис. 3.14, 3.15 получена динамика областей достижимости ведущего и цели соответственно в зависимости от параметров «партнера».

Анализ области показателя ведущего (см. рис. 3.14) при переборе параметров управлений цели показал, что среди параметров имеются заведомо худшие решения, которые не имеет смысла рассматривать при поиске векторного равновесия.

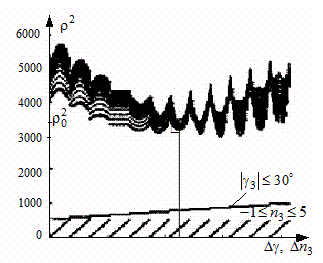
Рис. 3.14. Область достижимости показателя ведущего

Рис. 3.15. Область достижимости показателя цели

Как видно из рис. 3.14 и 3.15, области показателей перехватчика и цели выпуклы и имеют единственную точку равновесия (оптимальную как для перехватчика, так и для цели):

Данный метод позволил уменьшить сеть начальных приближений по вектору параметров. Был выбран достаточный диапазон изменения параметров, который составил около 20% от модульных значений в точке равновесия.

С учетом результатов, полученных в пунктах 3.5.1, 3.5.2, время вычислений алгоритмов уменьшилось в 60 раз. Некоторое повышение величины пролета при рассмотренных приближениях алгоритма является допустимым для задачи ближнего наведения ЛА и выгодным для противника.

3.5.3. Оценка эффективности параллельной реализации

Проведенные замеры времени выполнения отдельных блоков алгоритма выявили, что второй блок (поиск множества равновесных точек на ячейках сети) в процентном отношении (96,9%) является наиболее трудоемким.

Временная диаграмма, приведенная в табл. 3.5, получена с учетом оценки времени выполнения процедур на языках низкого уровня, которые, как правило, применяются в бортовых вычислительных комплексах.

Для оценки такта выдачи команд управления при распараллеливании программы на несколько транспьютеров целесообразно декомпозировать второй блок. Время вычисления процедур данного блока при небольшом числе транспьютеров будет обратно пропорционально их количеству. Структура вычислений в других блоках алгоритма не позволяет эффективно распараллелить их.

Таблица 3.5

Временные оценки этапов алгоритма

В следующей таблице дана приближенная оценка эффективности параллельной реализации процедур второго блока.

Таблица 3.6

Оценка параллельной реализации

Таким образом, рассмотренный в пунктах 3.4 и 3.5 пример применения алгоритма векторного равновесия в составе СТЭК-3 показывает его работоспособность для нелинейных систем высокого порядка.

Данный пример имеет практическую ценность, так как позволяет получить ПКЗУ управления коалиции ЛА в режиме ближнего наведения и намечает пути повышения быстродействия алгоритма для его реализации в БЦВМ.

1 Cм. сноску в п.1.2.