
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Алгоритм векторной оптимизации на основе конусов доминирования (эффективные решения)3.2.1. Сравнительный анализ методов векторной оптимизации Как правило (см. [206] и, например, [32]), основным понятием оптимальности в задачах векторной оптимизации является Парето-оптимальность, определение которой дано в свойствах коалиционного равновесия (опр. 3.6.) и в главе 1. Следует отметить, что векторная оптимизация с определением области Парето является частным подходом в общем классе кооперативных игр в характеристической форме, например [43, 199], где принципы оптимальности можно подразделить условно на два типа [32]: 1) оптимальность, связанная с устойчивостью поведения игроков (оптимальность по Парето, C-ядро и Н–М-решение); 2) оптимальность, которая явно или неявно предполагает наличие арбитра, формулирующего «разумные» свойства оптимального решения (арбитражная схема, среднеквадратическое решение, вектор дележа Шепли). Все эти подходы будут обсуждаться в главе 5. Здесь же основное внимание уделяется Парето-оптимизации как частного случая коалиционного равновесия. С учетом параметризации управляющих сил вида u = u(q, x), u = u(q, t), u = u(q) далее материал излагается на основе терминологии сравнительного анализа и результатов, полученных в обсуждаемых работах. Основная постановка имеет вид где Q(i) = {qÎQÌEr | qiÎQiÌEri; Из (3.7) следует, что необходимо определить значение векторного показателя Ji(q) на множестве Парето i-й коалиции Ki, максимальное в смысле отношения предпочтения Ri, варьируя лишь компоненты вектора qi. Остальные компоненты вектора q известны и фиксированы. Если предположить Ki = K = N, ММС составляет единую коалицию и задача (3.7) сводится к определению решений q, оптимальных по Парето (qП) относительно векторного показателя J(q).  Основой для выбора решений является анализ возможностей согласованного повышения эффективности коалиций в задачах проектирования и функционирования ММС. Ввиду сложности точного решения задачи (3.7) в связи с проблемой глобальной оптимизации Ji на множестве Q(i) предлагается двухэтапная процедура, первый этап которой – определение – является дискретной аппроксимацией задачи (3.7). Здесь При этом множество Задача (3.8) дает возможность сформировать начальные приближения для задачи (3.7) или для более сложной задачи из серии задач поиска коалиционного равновесия относительно набора коалиционных разбиений P и системы отношений предпочтения Ri, iÎMK в каждой коалиционной структуре РÌ Р. Если все показатели системы образуют единую коалицию или параметры всех коалиций, кроме одной, фиксированы, то получаем известную задачу Парето-оптимизации. Многокритериальные задачи математического программирования вида (3.7) являются частным случаем задачи многокритериального принятия решений [164]. Решение задачи (3.7) основано на построении компромисса с целью понижения неопределенности выбора на множестве Парето. Наиболее гибкой является диалоговая технология решения оптимизационных задач, особенно многокритериальных [17, 32, 48, 97, 105, 142, 220, 230, 263]. Разнообразие возможных способов получения и формализации информации о предпочтениях функционирующих коалиций или проектировщика в процессе диалога обусловило появление большого количества весьма различных подходов и методов решения многокритериальной задачи (3.7). Содержательные обзоры и библиографии по проблеме многокритериальной оптимизации представлены в работах 1. Процедуры, основанные на построении обобщенного скалярного показателя Ф = Ф(J, l) специального вида [5, 39, 83, 84, 120, 164], где l – вектор весовых коэффициентов, характеризующий относительную важность компонент векторного показателя J. Обычно на l накладывается условие нормировки: lÎL, где L = {lÎEm|li >0 "iÎM; В итоге исходная многокритериальная задача, например с показателем потерь J, сводится к обычной задаче нелинейного программирования: определить Легко показать [32, 83, 206], что если компоненты Ji показателя J, а также множество Q – выпуклые, то между множеством JG(Q) собственно эффективных (оптимальных по Джоффриону) [206] решений задачи (3.7) и множеством L вида (3.10) существует взаимнооднозначное соответствие. Таким образом, при заданной структуре функции Ф(J, l) вектор lÎL полностью определяет решение на множестве Парето. На каждой диалоговой итерации проектировщик производит коррекцию вектора l с тем, чтобы в конечном счете выйти на нужное решение. Отметим, что в (3.11) могут использоваться нормализованные значения показателей Ji. В этом случае на l, как правило, накладываются условия (3.10). Если же значения Ji не нормализуются, то вектор l играет более сложную роль, и для него условие (3.10) уже не выполняется. Кроме того, компоненты li имеют различные размерности, чтобы привести соответствующие Ji в свертке Ф(J, l) к безразмерному виду. Процедуры построения обобщенного показателя имеют ряд недостатков. Во-первых, сделать обоснованный выбор вектора l достаточно сложно, особенно при нелинейных показателях Ji, что чаще всего и бывает, так как проектировщику затруднительно формулировать свои предпочтения в терминах весовых коэффициентов. То есть неопределенность из области показателей переносится в область весовых коэффициентов (хотя диалоговый подход и уменьшает остроту этого вопроса, так как предоставляет возможность быстрой и многократной коррекции вектора l). Во-вторых, в случае невыпуклости множества Q или хотя бы одного Ji, iÎM, нарушается взаимнооднозначное соответствие между множествами L и JG(Q) [206]. Точнее говоря, перебор всех lÎL гарантирует построение лишь части множества JG(Q). В то же время на множестве JG(Q) можно выделить такие подмножества [83] , которые не являются решением задачи (3.11) ни при каких lÎL. Перечисленные недостатки существенно снижают ценность указанного подхода. 2. Процедуры с применением сообщений проектировщика о желаемых уровнях показателей.В [108, 207] рассматривается метод выделения главного показателя (пороговой оптимизации). В соответствии с этим методом из m показателей один выделяется в качестве главного (например, Ji), на остальные (m – 1) показателей накладываются ограничения. Исходная многокритериальная задача оказывается сведенной к задаче нелинейного программирования: определить где ej – максимально допустимое (пороговое) значение показателя Jj, eÎEm. Неопределенность в выборе главного показателя в задаче (3.12) преодолевается в [203] , где предлагается строить оптимизационные процедуры на основе принципа сложности [109, 204, 205, 240]. В [25] в качестве главного показателя рекомендуется использовать функционал сложности, а компоненты векторного показателя рассматривать, как m нелинейных ограничений вида (3.12б), сформированных на основе технических требований к системе. При этом изменяется смысл понятия оптимальности, и полученное решение не будет, вообще говоря, Парето-оптимальным относительно векторного показателя J. В [203] принцип минимальной сложности используется для систематического выбора задачи скалярной оптимизации (3.12) из всего набора так называемых сопряженных задач вида (3.12) при В [226, 361] в различных вариантах обсуждаются процедуры, основанные на идее целевого программирования, состоящей в нахождении решения, максимально приближенного к множеству одновременно не достижимых целей g в смысле определенной метрики, при ограничении на максимальные уклонения ci показателей Ji от целей gi для некоторых компонент вектора J. Здесь также все сводится к задаче нелинейного программирования. Варьирование параметров e, g, c в сеансах диалога позволяет выходить на различные точки множества Парето. Применение арбитражной схемы Нэша [32, 245] дает возможность целенаправленно выходить на множество Парето относительно точки J(q*), получая на нем решение J (qП), удовлетворяющее неравенству J (qП) £ J (q*), где в качестве q* принято выбирать минимаксное или равновесное по Нэшу решение. К недостаткам процедур, использующих информацию о желаемых уровнях показателей, следует отнести следующие: · введение дополнительных нелинейных ограничений, что усложняет задачу по сравнению с исходной постановкой; · неопределенность в назначении параметров, которые могут оказаться заниженными или недостижимыми. 3. Лексикографические процедуры многокритериальной оптимизации [144, 180, 206, 207], основная идея которых заключается в введении упорядоченности показателей по важности: J1 Обойти эту трудность позволяет метод последовательных уступок [38], в котором после решения очередной, i-й оптимизационной задачи назначается «уступка» Di на показатель Ji, расширяющая область допустимых решений последующей, (i+1)-й задачи. Окончательное решение зависит от вектора уступок и вида упорядоченности показателей по степени важности. К недостаткам метода последовательных уступок следует отнести следующие: · введение нелинейных ограничений; · сложность назначения обоснованной упорядоченности показателей по важности; · необходимость решения последовательности оптимизационных задач для получения одного варианта Парето-оптимального решения, что приводит к большим вычислительным издержкам. Проблема уменьшения размерности вектора показателей с исключением менее важных рассматривается в фундаментальной работе [180]. 4. Процедуры, основанные на информации о допустимых взаимных локальных изменениях показателей. Эти методы имеют прикладное значение, так как они [47, 230]: · формировались в рамках диалогового подхода и принципиально являются машинно-ориентированными; · используют более содержательную информацию о структуре предпочтений проектировщика без усложнения исходной постановки (3.7); · обеспечивают более целенаправленный поиск наилучшего компромисса по сравнению с упомянутыми выше типами процедур, особенно в случае бесконечного множества эффективных альтернатив. В [97] описывается метод Джоффриона (неявной функции полезности). Основным функциональным элементом метода является процедура построения в критериальном пространстве направления градиента Векторно-релаксационные методы [220, 265, 363] используют информацию о предпочтениях проектировщика в виде множества индексов MIÍM, содержащего номера компонент векторного показателя J, значения которых не должны ухудшаться по отношению к текущей ситуации J(q). Выбор направления спуска осуществляется методом, аналогичным методу возможных направлений Зойтендейка [110], используемому при оптимизации скалярных целевых функций и приводящему к задаче линейного или квадратичного программирования. Алгоритмы, приведенные в упомянутых работах, различаются видом условий нормировки искомого направления спуска, способом формирования множества Sa индексов активных ограничений, а также способом учета активных ограничений. В то время как метод Джоффриона описывает «динамику» изменения показателей по отношению лишь к опорному показателю, методы векторной релаксации позволяют учитывать взаимные изменения уже всех показателей, но в количественном отношении более грубо – с точностью до требования уменьшения или безразличия к величине показателя на основе формирования множества MI. Формирование точной информации о взаимных локальных изменениях показателей, как это делается, например, в методе Джоффриона при вычислении вектора коэффициентов замещения, предъявляет высокие квалификационные требования к проектировщику. Это естественно повышает трудоемкость решения задачи многокритериальной оптимизации. Для преодоления этого недостатка в ряде работ предлагается диалоговая процедура с лингвистическим моделированием предпочтений. Основная идея этого подхода заключается в том, что проектировщик производит оценку Парето-оптимальных решений, а также оценку необходимых изменений коэффициентов замещения в терминах лингвистической переменной [21]. Интенсивно развивается адаптивный подход к многокритериальным задачам, идейные истоки которого заключены в работах Я.З. Цыпкина. Согласно этому подходу [17, 115] решение задачи многокритериальной оптимизации интерпретируется, как процесс последовательного раскрытия неопределенности специального вида, а именно неопределенности формы компромисса. Адаптивным процедурам присущи все особенности методики случайного поиска [219]. Положительные стороны связаны с тем, что эти методы имеют простую реализацию, не требуют от векторного показателя практически никаких свойств, надежны и иногда оказываются более устойчивыми, чем градиентные методы. Однако процедуры случайного поиска имеют и недостатки, связанные с ограниченностью информации о свойствах компонент векторного показателя. Поэтому они оказываются в целом менее эффективными в тех случаях, когда градиентные процедуры применимы. 5. Процедуры, использующие понятия конуса доминирования и оптимальности по конусу[47, 48, 230, 312, 332, 428, 430] , обобщающие понятие оптимальности по Парето. В [428] поиск W-оптимального решения сводится к решению задачи математического программирования специального вида. При этом оставались открытыми вопросы обоснованного выбора вектора ограничений, вычисления конуса доминирования W. В [312] предлагается алгоритм построения конуса доминирования, как функции интервалов неопределенности весовых коэффициентов li компонент векторного показателя в свертке (3.11). Но указанный алгоритм применим лишь для случая, когда размерность критериального пространства В [312, 428] установлено, что вид конуса доминирования W определяет на множестве Парето JП(Q) подмножество JW(Q) Ì JП(Q) и, следовательно, W-оптимизация может улучшить неопределенность решения на множестве Парето. В работах В.А. Серова обосновано использование конуса доминирования в качестве универсальной конструкции для формализации предпочтений проектировщика в алгоритмах векторной оптимизации, разработаны методы проектирования на основе конусов доминирования. В частности, сформированы алгоритмы вычисления конусов доминирования, уточнены необходимые условия W- и Парето-оптимизации, предложены алгоритмы оптимизации по конусу с учетом выбора начального приближения на основе комбинации W-перебора и метода зондирования пространства параметров. 6. Как было отмечено ранее, задача векторной оптимизации является одной из частных задач теории кооперативных игр. Некоторые вопросы исследования задачи управления ММС как кооперативной игры в форме характеристической функции будут рассмотрены в главе 5. В обзорах [28, 248] предлагается краткий неполный перечень работ в направлении кооперативных игр. Так, в обзоре [248] и в работе [32] в числе других рассматриваются вопросы применения арбитражных схем и среднеквадратичных решений в кооперативной игре. Геометрические свойства и структура Парето-области исследуются в работе [281]. Получение решения кооперативной игры в форме характеристической функции как С-ядра рассматривается в работах [35, 170]. Принципиальные вопросы вступления в коалицию-кооперацию с объединением целей и ресурсов и обеспечением определенной устойчивости коалиций-коопераций рассмотрены в фундаментальных работах 3.2.2. Понятие конуса доминирования W. Необходимые условия Парето- и W-оптимизации Определение 3.14 [47, 428]. Если каждой точке поставить в соответствие множество D(z) доминирующих факторов, такое что для B = {zÎEm | и где множество { Определение 3.15 [428, 477]. Точка z*ÎJ(Q) называется W-оптималь-ной (оптимальной по конусу W), если не существует zÎ J (Q), z¹ z*, такого что (z – z*)ÎW. Для полной физической картины полезно привести следующие утверждения из [428] и [312] соответственно. Утверждение 3.3 [428]. Если W1Ì W2, то где Утверждение 3.4. [312] Пусть W-многогранный конус, определенный матрицей B, W = {zÎEm | Bz£ OP}. Пусть H(q)ÎEP и H(q) = BJ(q). Тогда эффективные (оптимальные по Парето) решения для векторного показателя H(q) точно совпадают с W-оптимальными решениями для векторного показателя J(q) на множестве Q: т.е. конус определяет часть множества Парето-решений. Следствие 3.1. Из утверждения 3.4 следует, что т.е. «прямоугольный» конус доминирования определяет все множество Парето-решений. Из определения 3.15 следует слабая оптимальность по конусу. Определение 3.16 [213]. Решение J* = J(q*) называется слабо оптимальным по конусу W с матрицей B= [p´m] в критериальном пространстве Em векторного показателя J, если не существует такого qÎQ, для которого справедлива система неравенств B(J(q) – J(q*)) < O P. (3.16) Из (3.15) и утверждения 3.4 следует, что слабая оптимальность по конусу W эквивалентна слабой оптимальности по Парето [206] в критериальном пространстве EP показателя H = BJ. На основе подхода Куна–Таккера–Мукая [363] и с учетом известной теоремы Да Канхи–Поллака–Джоффриона [206] в [213, 230] сформулированы необходимые условия слабой оптимальности по конусу. Утверждение 3.5. Пусть q* – оптимальное решение по конусу доминирования W относительно целевого вектора Jи множества Q, заданного в виде Q = {qÎEr | G(q) £ 0}, где G(q) = {gi(q)£0, Функционал Тогда является совместной система уравнений
Следствие 3.2. Так как множество слабо оптимальных по конусу решений содержит в себе множество оптимальных по конусу решений, то условие (3.17) является также необходимым условием оптимальности по конусу. Следствие 3.3. Как следует из (3.14), (3.15), при B = E условие (3.17) превращается в необходимое условие Парето-оптимальности q*. 3.2.3. Об алгоритмах вычисления конусов доминирования В [47, 213, 230] сформировано несколько вариантов вычисления конусов доминирования в рамках задач векторной оптимизации, в которых учитываются: · требование проектировщика о допустимых взаимных локальных изменениях показателей; · равномерное улучшение компонент векторного показателя; · неопределенность весовых коэффициентов компонент векторного показателя. Все данные алгоритмы имеют универсальный характер на классе задач и прикладную ценность. Третий вариант оптимально учитывает условия неопределенности, его конструкция и приложения даны в работе [213]. Второй вариант используется, например, для построения модифицированной арбитражной схемы в условиях обязательных соглашений (см. главу 6). Первый вариант вычисления конуса как функции матрицы коэффициентов замещения рассматривается далее, как основной при формировании алгоритмического обеспечения W-оптимизации. Данный алгоритм является обобщением известного алгоритма Джоффриона [97], общий смысл которого рассмотрен в 3.2.1 и имеет следующую структуру: Шаг 1. Формирование множества K = {1 £ k1 £ k2£...£ kp £ m} индексов компонент векторного показателя, изменение величин которых намечено контролировать. Шаг 2. Построение прямоугольной матрицы A размером [p´m] с элементами aij вида: где 0 £ Шаг 3. Построение конуса доминирования в виде W = {zÎEm | Bz£ OP}, (3.19) где B = A. То есть конус {ai = [ai1,...,aim]T, составленных из строк матрицы A вида (3.18). Сформулируем следующее Утверждение 3.6 [213]. Пусть задана система предпочтений в форме матрицы A вида (3.18). Тогда: 1) конус доминирования W вида (3.19) является выпуклым, острым, многогранным; 2) для любых удовлетворяет условию Замечание 3.1. Геометрический смысл утверждения 3.6 состоит в том, что вектор d, определяемый в виде (3.21), для любых Замечание 3.2. Гиперплоскость П, касательная к поверхности равных значений неявной функции полезности в методе Джоффриона, является частным случаем конуса доминирования, построенного в соответствии с (3.18), (3.19). Касательной гиперплоскости с опорным показателем Ji соответствует матрица A = WT, где компоненты Wj вектора W представляют собой коэффициенты замещения, вычисленные по алгоритму Джоффриона. Замечание 3.3. В терминах конуса доминирования W, удовлетворяющего соотношениям (3.18), (3.19), можно интерпретировать информацию о предпочтениях проектировщика в методах векторной релаксации, обсуждавшихся в разделе 3.2.1 [213, 220, 230, 265, 363]. Если в (3.18) для всех iÎK, jÎM, j¹i положить aij = 0, то полученный конус доминирования реализует требование одновременного неухудшения компонент векторного показателя Jс номерами из множества K, сформированного на шаге 1 алгоритма. Значения компонент вектора J с номерами из множества (M\K) при этом контролироваться не будут. Условие K = M означает требование одновременного неухудшения всех компонент вектора J. В этом случае конус доминирования W превращается в неположительный ортант Таким образом, вычисление конуса доминирования в виде (3.18), (3.19) дает возможность количественно учитывать более содержательную информацию о предпочтениях проектировщика по сравнению c методами Джоффриона и векторной релаксации при решении задач (3.7). Второй вариант конструкции конуса доминирования изложен в главе 6, где он используется для формирования модифицированной арбитражной схемы в условиях обязательных соглашений. Третий вариант возникает, если появляется сложность точного назначения вектора весовых коэффициентов lÎL, где L задана в форме (3.10) при свертке векторного показателя, но имеется интервальная информация: где lL = [lL1,...,lLm]T, lH = [lH1,...,lHm]T. Информацию вида (3.23) о векторе l можно интерпретировать при В работе [213] формируется машинно-ориентированный алгоритм вычисления матрицы B конуса доминирования W, позволяющий решать задачу для любого m. Очевидно, что практически важным частным случаем (3.23) является формирование матрицы B как пересечения наборов l, удовлетворяющих ограничениям (3.23) и имеющим вид 3.2.4. Алгоритмическое обеспечение задачи оптимизации Предполагается, что конус доминирования W задан в виде (3.19) и фиксирован. Для простоты обозначений будем предполагать, что компоненты показателя потерь J и компоненты вектора параметров qобразуют единые коалиции интересов и действия соответственно. Поэтому задачу (3.7) можно записать в виде (J – вектор потерь): определить где J(q)ÎEm, qÎEr, R = { Q = {qÎEr | qL£ q£ qH, Cq£ b}, (3.25) C = [s´r], b = [s´1]. Для формирования алгоритма поиска W-оптимального решения в задаче (3.24) в [213] видоизменяется известный алгоритм векторной релаксации [265] с учетом конуса доминирования (3.19). Вычислительная процедура представляется в виде последовательности следующих этапов [213]. Выбор направления спуска внутри конуса доминирования. Как следует из [213, 312, 428], условие доминирования решения BDJ £ O, (3.26) где D J = Использование соотношения (3.26) в качестве условия спуска в алгоритме векторной релаксации позволяет сформулировать задачу выбора направления спуска внутри конуса доминирования в виде: где (3.27б) – условие dÎW; (3.27в) – условие того, что вектор d направлен вовнутрь области допустимых значений параметров Q вида (3.25); Постановка задачи выбора направления вида (3.27) является более общей по сравнению с постановками [265, 363], которые могут быть получены из (3.27) как ее частные случаи. Для этого матрицу B конуса доминирования W необходимо задать с помощью первого алгоритма в виде функции коэффициентов замещения. Для получения условий останова при решении задачи (3.27) сформулировано утверждение: Утверждение 3.7 [213]. Пусть в точке q выполнены условия регулярности [220]: существует такая точка q*ÎEr, что справедлива система неравенств Aaq*>O (матрица Aa определена в (3.27)). Тогда: · точка q удовлетворяет необходимым условиям слабой оптимальности по конусу W тогда и только тогда, когда оптимальное значение целевой функции zв задаче (3.27) равно 0; · если z> 0, то решение d задачи (3.27) принадлежит конусу доминирования WQ, построенному в пространстве параметров Er. Необходимо отметить, что решение задачи (3.27) зависит от условий нормировки (3.27г). В вычислительной практике, как правило, используются [18, 110] следующие виды нормировки: при K = ¥ |di|£1, при K = 2 dTd£ 1. (3.28б) В результате получаем задачу линейного программирования вида: где G – вспомогательный вектор, с помощью которого осуществляется переход от переменной d к неотрицательной вспомогательной переменной Для решения задачи (3.29) используется симплекс-метод. Более точное решение задачи (3.27), улучшающее сходимость алгоритма W-оптимизации в целом, можно получить, учитывая условия нормировки вида (3.28б). Однако это условие превращает задачу (3.27) в нелинейную и требует иных подходов к ее решению. В работе [47] задача W-оптимизации в нелинейном варианте решается на основе объединения и обобщения результатов [8, 110, 363]. В итоге от задачи (3.27) переходим к линейной задаче дополнительности относительно переменных u, v: где Решение задачи (3.31) осуществляется с помощью алгоритма дополнительного ведущего преобразования Лемке [8], после чего легко вычисляется вектор d. Как доказывается в [8], алгоритм Лемке сходится к решению задачи (3.31) за конечное число шагов, если матрица H является сильно коположительной. Матрица H в (31) является сильно коположительной. Действительно, во-первых, H – симметричная матрица и, следовательно, коположительная. Во-вторых, Таким образом, построены эффективные вычислительные процедуры выбора направления спуска внутри конуса доминирования, решающие поставленную задачу за конечное число шагов, и дающие возможность формализовать информацию о предпочтениях проектировщика в виде матриц многогранных конусов доминирования. Вычисление шаговой длины в выбранном направлении. Вычисление шаговой длины 1. Выбор DJ(k)ÎW, (3.32) где DJ(k) = J(k +1) – J(k); J(k +1) = J(q(k)+ В том случае, когда W – многогранный конус вида (3.19), условие (3.32) представляет собой систему неравенств вида (3.26). 2. Вычисление где Шаговая длина где Таким образом, процедуру поиска оптимального решения в [213] предлагается рассматривать в виде последовательности следующих основных этапов, составляющих в совокупности одну диалоговую итерацию: · формирование конуса доминирования; · выбор направления спуска внутри конуса доминирования; · вычисление шаговой длины в выбранном направлении. Некоторые виды комплексирования систем управления при решении технических задач приводят к появлению разрывности компонент векторного показателя исследуемой системы. Это обстоятельство требует модификации построенной выше процедуры W-оптимизации с учетом указанного свойства. При этом используется подход к решению задач оптимизации разрывных показателей, изложенный в [16]. В [16] формируются численные методы поиска экстремума разрывных показателей, по своему содержанию аналогичные известным градиентным методам для непрерывно дифференцируемых показателей. Показано, что для этого необходимо в соответствующих методах для непрерывно дифференцируемых функций использовать вместо градиента понятие аппроксимационного градиента. 3.2.5. Выбор начального приближения в задаче многокритериальной оптимизации (постановка (3.8)) Как известно, для векторного показателя J(q) общего вида, когда некоторые его компоненты, вообще говоря, являются невыпуклыми на Q функциями, на множество достижимых векторных оценок J(Q) могут существовать локально эффективные точки, не принадлежащие глобальному множеству Парето JП(Q). В этих точках также выполняются необходимые условия W-оптимальности (17). Поэтому неудачное расположение начального приближения в задаче (7) может привести к неправильному результату вследствие преждевременного останова алгоритма W-оптимизации в локально эффективной внутренней точке множества J(Q). С другой стороны, при решении задачи Нэш-оптимизации (глава 2) в случае неединственности равновесия по Нэшу необходимо на множестве равновесных решений определить недоминируемые точки, т.е. ближайшие к множеству Парето [32]. В этом случае начальное приближение целесообразно назначать в окрестности множеств Парето, что повышает возможность определения недоминируемого равновесного решения. Таким образом, выбор начального приближения является важным фактором, влияющим на эффективность вычислительных процедур и правильность получаемых результатов. Постановку задачи выбора начального приближения на основе (3.8) предлагается формализовать в виде [48, 213]: определить где Q(i) = {qÎEr | qiÎQi; То есть необходимо определить множество Если положить i = MK\j, то можно оценивать конфликтное взаимодействие коалиции Kj и контркоалиции Ki. В данном разделе для решения задачи (3.35) предлагается использовать известный метод зондирования пространства параметров, основанный на методике ЛП-поиска [238]. В этом методе условно можно выделить два основных этапа: 1) составления таблицы испытаний; 2) оптимизация таблицы испытаний. Для определенности полагаем, что Этап 1. Генерируется последовательность точек {p(i)}, равномерно распределенная в r-мерном единичном кубе. Как обосновывается в [238], наилучшими характеристиками равномерности обладают так называемые ЛПt-последовательности. Для генерации ЛПt-последовательности в [238] предлагается арифметический алгоритм, использующий специальную таблицу направляющих чисел. После этого с помощью линейного преобразования L, сохраняющего равномерность распределения, преобразуем множество сгенерированных точек {p(i), Пq = L(Пp). (3.36) Преобразование L задается [238] в виде Так как в описании области Q используются линейные ограничения общего вида, то в каждой точке q(i) необходимо проверять выполнение системы неравенств Cq(i) £ b. Если q(i) является допустимой, то в ней вычисляется значение векторного показателя J(q(i)) и заносится в таблицу испытаний. Этап 2. Предлагается алгоритм оптимизации таблицы испытаний по конусу доминирования W, заданному в виде (19). Для этого из таблицы испытаний выбирается какая-либо точка q(i) и помечается. Просматривая все точки q(j) таблицы испытаний, отличные от q(i), исключим те из них, для которых B(J(q(j)) – J(q(i))) ³ O, (3.38) причем хотя бы одно из неравенств строгое. То есть проверяется принадлежность точек Dij конусу (– W); Dij = J(q(j)) – J(q(i)). Затем среди оставшихся точек выбирается непомеченная, и вновь повторяется процесс исключения по правилу (3.38). После конечного числа шагов останутся только такие помеченные точки, которые являются дискретной аппроксимацией множества W-оптимальных решений. Второй этап данного алгоритма [213] отличается от [238] более общей постановкой, основанной на использовании понятия конуса доминирования. В случае B = E оптимизация таблицы испытаний приведет к построению дискретной аппроксимации всего множества Парето, что соответствует максимальной неопределенности весовых коэффициентов O£ l £ 1. В случае B ¹ E, когда O£ lL £ l £ lH £ 1, W-оптимизация позволяет построить подмножество В приложениях, как правило, с увеличением плотности ЛПt-сети дискретная аппроксимация 3.3. Алгоритмы определения векторного равновесия В соответствии с понятиями коалиционного равновесия, изложенными в разделе 3.1, формулировка вида коалиционного равновесия определяется тремя степенями свободы: · множество коалиционных разбиений P; · вид V-решения; · степенью «охвата» Парето-области коалиции. На основе определения 3.9 векторное равновесие по Нэшу является частным случаем коалиционного равновесия при единственном коалиционном разбиении, отсутствии угроз (частный случай V-решений) и принадлежности к полной Парето-области коалиции. В соответствии определением 3.11 W-равновесие является частным случаем векторного равновесия по Нэшу, так как формулируется на части Парето-области коалиции. С другой стороны, при применении единой технологии решения обеих задач, например, на основе конусов доминирования, необходимые условия и алгоритмы определения близки. Поэтому имеет смысл объединить оба определения (3.9), (3.11) в рамках единой схемы поиска векторного равновесия. 3.3.1. Необходимые условия векторного равновесия Раскрывая необходимое условие W-оптимальности (3.17), можно получить где m, v³0, m ¹ 0; Ga – переобозначение активных ограничений. Как известно, при B = E данное условие дает необходимое условие Парето-оптимальности. Формирование постановки (3.7) для каждого iÎMK и совместных необходимых условий (3.39) для всех i приводит к следующему утверждению: Утверждение 3.8 [47]. Пусть qr – векторное равновесное решение. Тогда является совместной система равенств |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 960. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
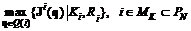 , (3.7)
, (3.7)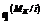 – фиксированы}; Ji(q) – векторный показатель эффективности i-й коалиции; MK – множество коалиций коалиционного разбиения P ММС, состоящей из N объектов; Q(i) – множество параметров i-й коалиции; Ri – отношение предпочтения на подмножестве
– фиксированы}; Ji(q) – векторный показатель эффективности i-й коалиции; MK – множество коалиций коалиционного разбиения P ММС, состоящей из N объектов; Q(i) – множество параметров i-й коалиции; Ri – отношение предпочтения на подмножестве 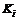 .
.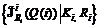 (3.8)
(3.8)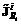 – дискретная аппроксимация множества Парето-оптима-льных в смысле Wi (3.7) значений
– дискретная аппроксимация множества Парето-оптима-льных в смысле Wi (3.7) значений 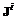 .
.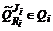 .
.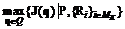 (3.9)
(3.9)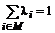 }. (3.10)
}. (3.10)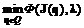 . (3.11)
. (3.11)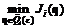 ; (3.12а)
; (3.12а)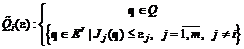 , (3.12б)
, (3.12б)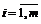 . Каждая из сопряженных задач характеризуется некоторым значением Wi,
. Каждая из сопряженных задач характеризуется некоторым значением Wi, 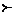 J2
J2 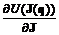 функции полезности U в текущей точке J(q). При этом, однако, функцию U(J) не требуется задавать в явном виде. Предлагается строить гиперплоскость П(J) = 0, касательную к поверхности равных значений неявной функции полезности U(J) в точке J(q). Компоненты вектора W, нормального к касательной гиперплоскости П, формируются после назначения опорного показателя Ji. Величина Wj характеризует эквивалентные изменения показателей Ji и Jj (при постоянстве значений других показателей), не меняющие значения неявной функции полезности и определяющие относительную важность для проектировщика i-го показателя по сравнению с j-м в текущей точке J(q). Далее полагается
функции полезности U в текущей точке J(q). При этом, однако, функцию U(J) не требуется задавать в явном виде. Предлагается строить гиперплоскость П(J) = 0, касательную к поверхности равных значений неявной функции полезности U(J) в точке J(q). Компоненты вектора W, нормального к касательной гиперплоскости П, формируются после назначения опорного показателя Ji. Величина Wj характеризует эквивалентные изменения показателей Ji и Jj (при постоянстве значений других показателей), не меняющие значения неявной функции полезности и определяющие относительную важность для проектировщика i-го показателя по сравнению с j-м в текущей точке J(q). Далее полагается 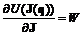 .
.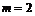 . Таким образом, в существующем виде процедуры W-оптимизации оказываются мало пригодны и с практической точки зрения.
. Таким образом, в существующем виде процедуры W-оптимизации оказываются мало пригодны и с практической точки зрения.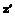 ÎJ(Q) (
ÎJ(Q) ( 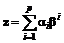 , ai³0,
, ai³0, 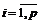 } (3.13)
} (3.13)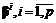 } называется множеством экстремальных векторов конуса B.
} называется множеством экстремальных векторов конуса B.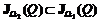 ,
,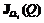 означает множество всех Wi-оптимальных точек в J (Q).
означает множество всех Wi-оптимальных точек в J (Q).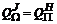 , (3.14)
, (3.14)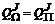 при B = E, (3.15)
при B = E, (3.15)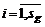 ; Cq£ b, C = [sc, r], b = (sc´1), qL £ q£ qH }.
; Cq£ b, C = [sc, r], b = (sc´1), qL £ q£ qH }.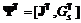 дифференцируем по Фреше в точке q*, где s – множество индексов ограничений G, активных в точке q*.
дифференцируем по Фреше в точке q*, где s – множество индексов ограничений G, активных в точке q*.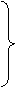
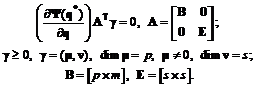 (3.17)
(3.17)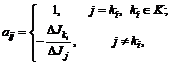 (3.18)
(3.18)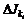 – максимально допустимое ухудшение показателя
– максимально допустимое ухудшение показателя 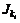 , соответствующее улучшению показателя
, соответствующее улучшению показателя 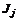 на
на 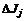 (если значения других показателей при этом не изменяются). На величины
(если значения других показателей при этом не изменяются). На величины 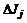 , kiÎK, jÎM, наложены ограничения, обусловленные постановкой задачи (3.7) в виде задачи минимизации:
, kiÎK, jÎM, наложены ограничения, обусловленные постановкой задачи (3.7) в виде задачи минимизации: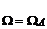 , где WA – конус, натянутый на систему векторов
, где WA – конус, натянутый на систему векторов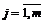 вектор dÎW, координаты dl,
вектор dÎW, координаты dl, 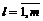 которого вычисляются в виде
которого вычисляются в виде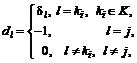 (3.21)
(3.21)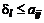 . (3.22)
. (3.22)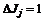 показателя
показателя 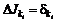 показателя
показателя 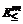 критериального пространства Em, что означает [213, 312, 428] совпадение понятий W-оптимальности и Парето-оптимальности.
критериального пространства Em, что означает [213, 312, 428] совпадение понятий W-оптимальности и Парето-оптимальности.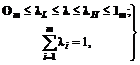 (3.23)
(3.23)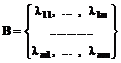 . (3.23а).
. (3.23а).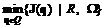 , (3.24)
, (3.24)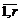 }. Область Q определяется, например, как
}. Область Q определяется, например, как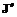 над решением
над решением 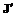 относительно конуса W с матрицей B записывается в виде
относительно конуса W с матрицей B записывается в виде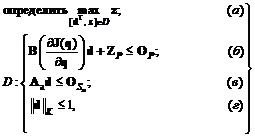 (3.27)
(3.27)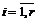 , (3.28а)
, (3.28а)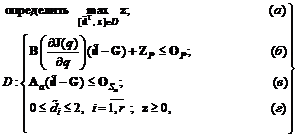 (3.29)
(3.29)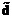 , необходимой для решения задачи (3.27):
, необходимой для решения задачи (3.27):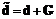 . (3.30)
. (3.30)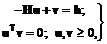 (3.31)
(3.31)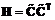 ;
; 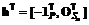 ;
;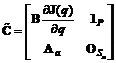 .
.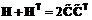 . Поэтому из равенства zTHz = 0 следует, что (H + HT)z = 0.
. Поэтому из равенства zTHz = 0 следует, что (H + HT)z = 0.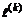 в выбранном направлении
в выбранном направлении 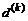 на k-й итерации принципиально может производиться с помощью алгоритмов, аналогичных алгоритмам одномерной минимизации, используемым в задачах условной оптимизации скалярных целых функций. Анализ алгоритмов одномерной оптимизации можно найти в [186]. Учет свойства многокритериальности и использование понятие W-оптимальности требуют модификации существующих алгоритмов, так как при этом изменяется вид условия спуска [312, 428]. Рассмотрим алгоритмы вычисления шаговой длины следующих двух типов.
на k-й итерации принципиально может производиться с помощью алгоритмов, аналогичных алгоритмам одномерной минимизации, используемым в задачах условной оптимизации скалярных целых функций. Анализ алгоритмов одномерной оптимизации можно найти в [186]. Учет свойства многокритериальности и использование понятие W-оптимальности требуют модификации существующих алгоритмов, так как при этом изменяется вид условия спуска [312, 428]. Рассмотрим алгоритмы вычисления шаговой длины следующих двух типов.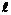 (k)d(k)); J(k) = J(q(k)).
(k)d(k)); J(k) = J(q(k)).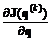 , вычисляемых на предыдущих итерациях для целевого выбора направления
, вычисляемых на предыдущих итерациях для целевого выбора направления 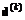 в задаче (3.27) (так как специально для выбора
в задаче (3.27) (так как специально для выбора 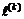 это делать нерационально). В соответствии с [312, 428] условие спуска (3.26) означает одновременное уменьшение всех компонент векторного показателя H = BJ. Тогда спуск вдоль выбранного направления d(k) целесообразно проводить до ближайшего минимума одной из компонент векторного показателя H или до выхода на границу области допустимых значений параметров Q. При решении этой задачи могут быть использованы обычные методы одномерной минимизации (метод Фибоначчи, золотого сечения, параболической интерполяции и др.) [8, 186]. Метод параболической интерполяции обобщается на случай задачи W-оптимизации следующим образом. Легко показать, что вектор
это делать нерационально). В соответствии с [312, 428] условие спуска (3.26) означает одновременное уменьшение всех компонент векторного показателя H = BJ. Тогда спуск вдоль выбранного направления d(k) целесообразно проводить до ближайшего минимума одной из компонент векторного показателя H или до выхода на границу области допустимых значений параметров Q. При решении этой задачи могут быть использованы обычные методы одномерной минимизации (метод Фибоначчи, золотого сечения, параболической интерполяции и др.) [8, 186]. Метод параболической интерполяции обобщается на случай задачи W-оптимизации следующим образом. Легко показать, что вектор 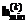 экстремумов интерполирующих парабол вычисляется по формуле
экстремумов интерполирующих парабол вычисляется по формуле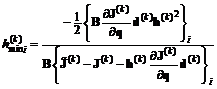 , (3.33)
, (3.33) ;
;  ;
; 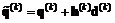 ;
; 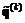 – вспомогательная точка, необходимая для построения интерполирующей параболы;
– вспомогательная точка, необходимая для построения интерполирующей параболы; 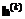 задается отдельно.
задается отдельно.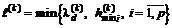 , (3.34)
, (3.34)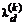 – расстояние от точки
– расстояние от точки 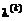 до границы допустимой области Q в направлении
до границы допустимой области Q в направлении 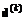 . Необходимо отметить, что другие методы одномерной оптимизации обобщаются на задачу W-оптимизации аналогично.
. Необходимо отметить, что другие методы одномерной оптимизации обобщаются на задачу W-оптимизации аналогично.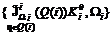 , (3.35)
, (3.35)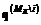 = const}.
= const}.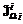 значений показателя
значений показателя 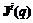 , являющееся дискретной аппроксимацией множества Wi-оптимальных решений (в частном случае – множества Парето). При этом аналогичное множество определяется в пространстве параметров:
, являющееся дискретной аппроксимацией множества Wi-оптимальных решений (в частном случае – множества Парето). При этом аналогичное множество определяется в пространстве параметров: 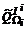 . Если положить
. Если положить 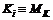 , то получим
, то получим  , Q(i) = Q. Для конуса доминирования при этом полагаем
, Q(i) = Q. Для конуса доминирования при этом полагаем 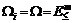 . Тогда задача (3.35) будет интерпретироваться, как построение дискретной аппроксимации множества Парето относительно векторного показателя JÎEm и вектора параметров qÎQÌEr.
. Тогда задача (3.35) будет интерпретироваться, как построение дискретной аппроксимации множества Парето относительно векторного показателя JÎEm и вектора параметров qÎQÌEr.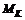 .
.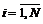 }ÎПp в множество точек {q(i),
}ÎПp в множество точек {q(i), 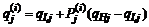 . (3.37)
. (3.37)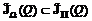 и на этапе экспертного анализа работать с сокращенной таблицей, в которую не будут входить заведомо неприемлемые варианты. Время оптимизации таблицы испытаний уменьшается с сокращением интервалов неопределенности весовых коэффициентов.
и на этапе экспертного анализа работать с сокращенной таблицей, в которую не будут входить заведомо неприемлемые варианты. Время оптимизации таблицы испытаний уменьшается с сокращением интервалов неопределенности весовых коэффициентов.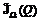 множества
множества 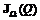 приближается к нему и, начиная с некоторого N, практически не изменяет своего положения и конфигурации. Это обстоятельство позволяет проводить исследование при ограниченном числе зондирующих точек, что сокращает вычислительные затраты.
приближается к нему и, начиная с некоторого N, практически не изменяет своего положения и конфигурации. Это обстоятельство позволяет проводить исследование при ограниченном числе зондирующих точек, что сокращает вычислительные затраты.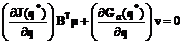 , (3.39)
, (3.39)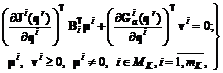 (3.40)
(3.40)